大林算法仿真分析：探究其优化效果

【例6-13】大林算法仿真仪。

大林算法仿真分析仪程序如shixz06_13所示。其程序框图面板和前面板分别如图6-6-2和图6-6-3所示。

（1）纯滞后二阶惯性被控对象和期望闭环传递函数离散化模型

用户在前面板上按照式（6-6-1）和式（6-6-2）设定二阶系统时间常数T₁，T₂，延迟时间tao，增益K，采样周期T_s和期望时间常数T_h，离散化程序段如下：

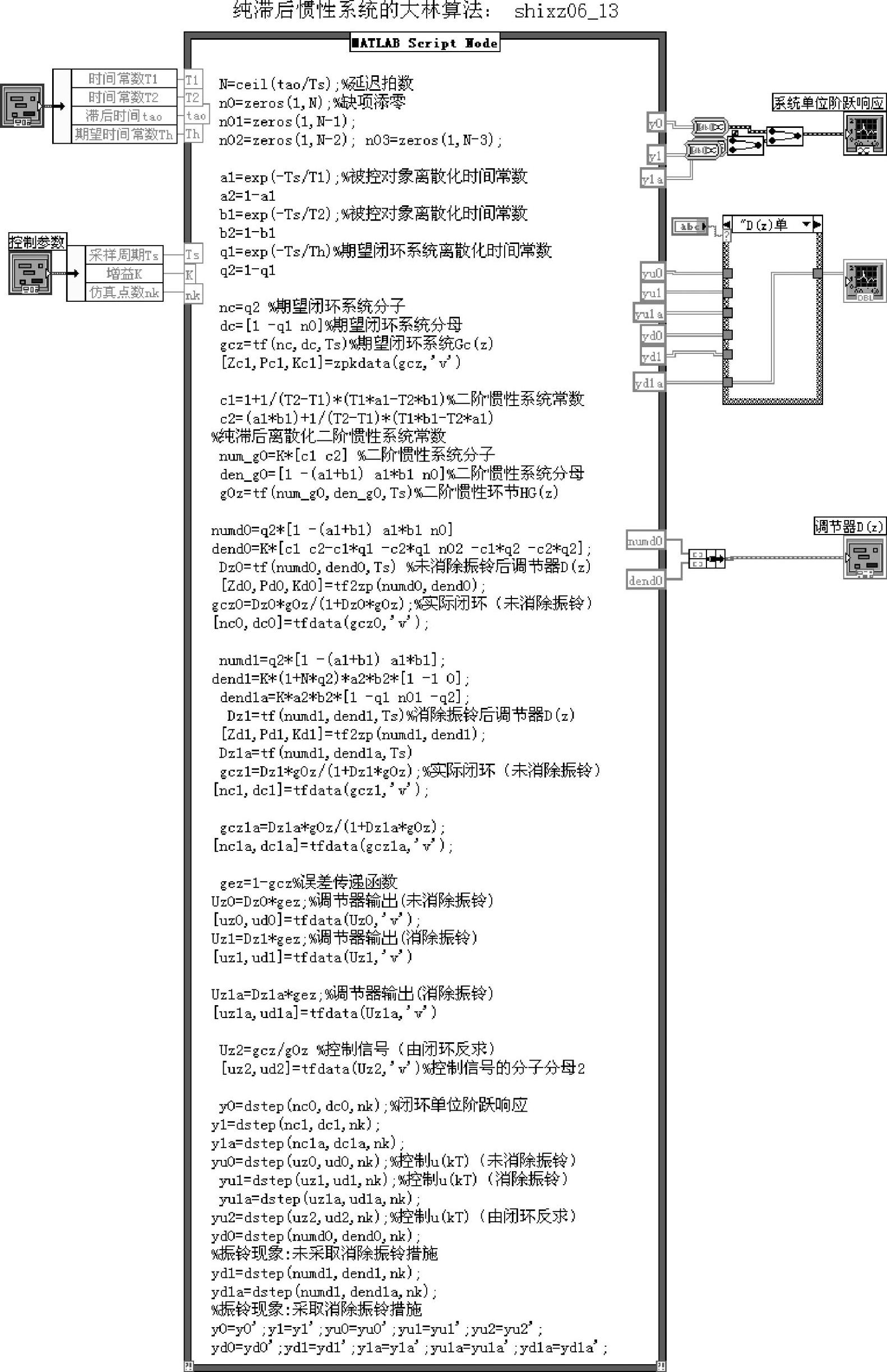
图6-6-2 程序shixz06_13框图面板

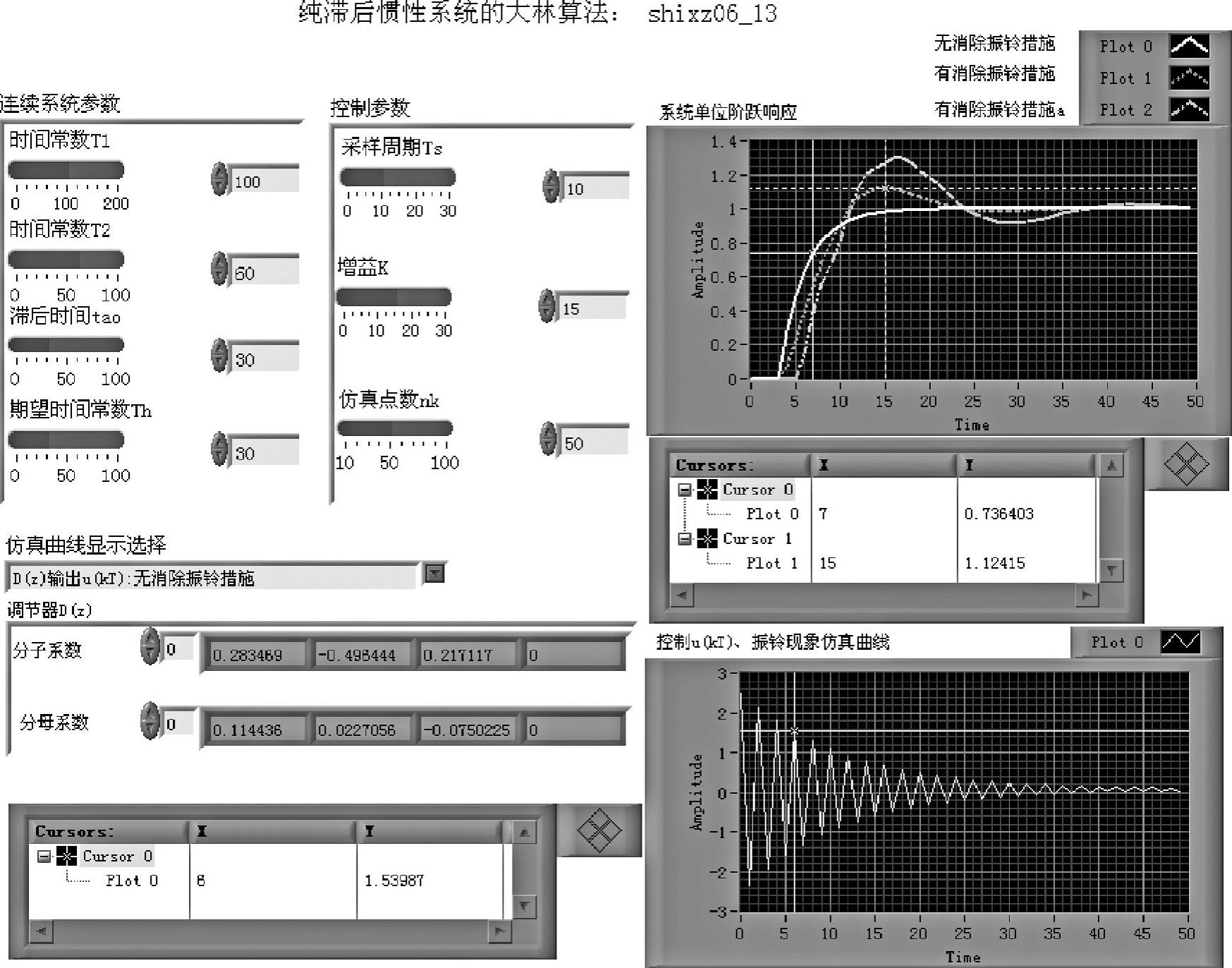
图6-6-3 程序shixz06_13前面板

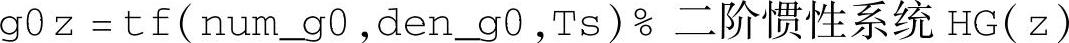
运行后，实例期望闭环系统式（6-6-3）（gcz）为

广义被控对象式（6-6-4）（g0z）为

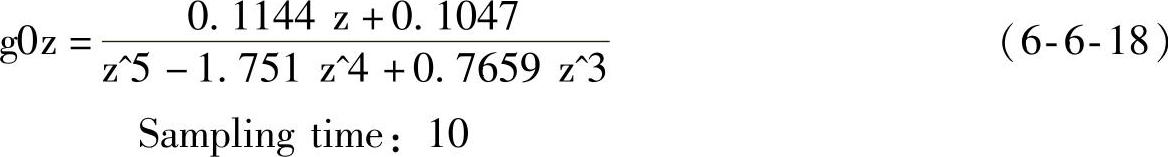
读者还可以使用命令c2d获得无延迟部分的离散化模型。

（2）无消除振铃措施的调节器D（z）（Dz0）

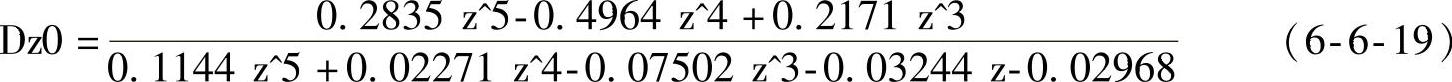
（3）有消除振铃措施的调节器D（z）

(www.xing528.com)

（4）实际闭环传递函数

（5）调节器的输出U（z）

（6）输出、控制及振铃的时域数值

图6-6-3的系统单位阶跃响应示波器上绘制了3条响应曲线。曲线plot0对应的闭环使用调节器式（6-6-11），未采用消除振铃措施；曲线plot1对应的闭环使用调节器式（6-6-16），消除了部分振铃极点；曲线plot2对应的闭环使用调节器式（6-6-15），消除了全部振铃极点。它们的稳态特性相同，但其瞬态特性不同，未消除振铃极点的响应无超调，最符合纯滞后惯性被控对象控制的初衷要求。采用消除全部振铃极点的调节器，其闭环响应出现较大超调和一次振荡。消除部分振铃极点的瞬态特性居于二者之间。造成这种情况的原因在于，使用未消除振铃的调节器构成实际闭环系统时，可以还原成期望闭环传递函数，实际上曲线plot0就是期望闭环传递函数的单位阶跃响应。而消除振铃极点之后的调节器构成闭环时与期望闭环有一定误差，使其输出响应也与期望闭环响应产生差距。

系统的控制u（kT）和调节器的单位阶跃响应示于第二个示波器上。可以使用图6-6-4的选择开关选择需要显示的曲线。

几种不同振铃现象的仿真曲线如图6-6-5～图6-6-7所示。根据振铃幅度的定义式（6-6-12），图6-6-5～图6-6-7的振铃幅度依次为4.8297，0.5252和0。附带说明，调节器的输出（控制）和调节器的单位阶跃响应（振铃）的最初几拍具有相同的幅值，但随着拍数的增加，二者出现差别。读者可以通过仿真仪的显示曲线选择加以研究。

程序shixz06_13a示出了使用阶梯波显示曲线的大林算法，可供参考。

图6-6-4 仿真曲线显示选择开关

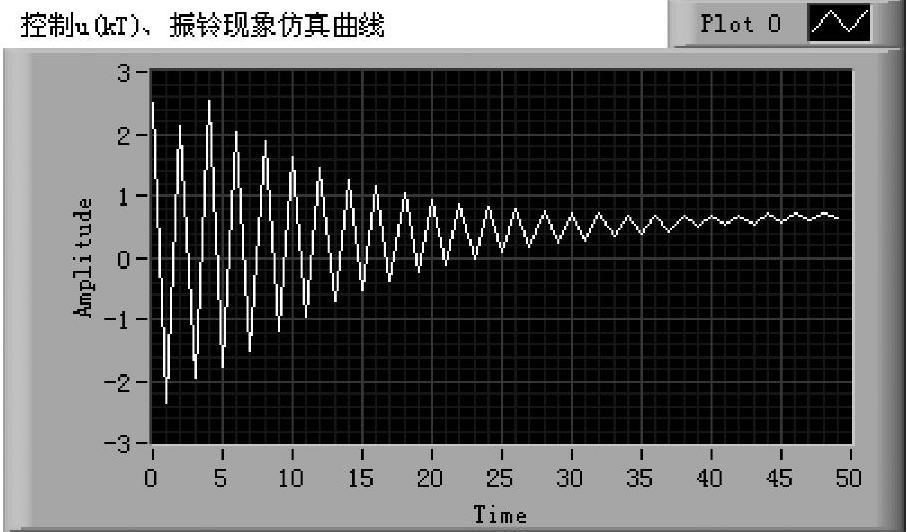
图6-6-5 无消除振铃措施的u（kT）

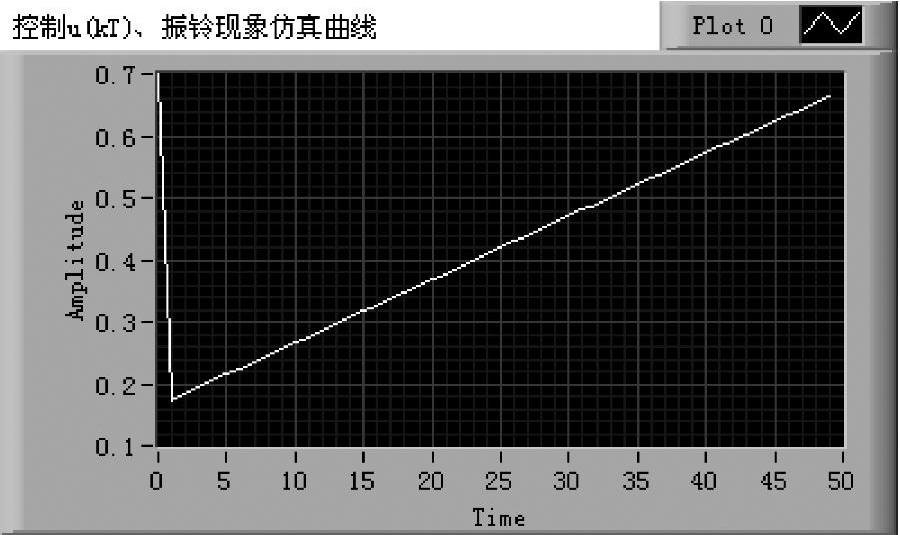
图6-6-6 消除部分振铃极点的u（kT）

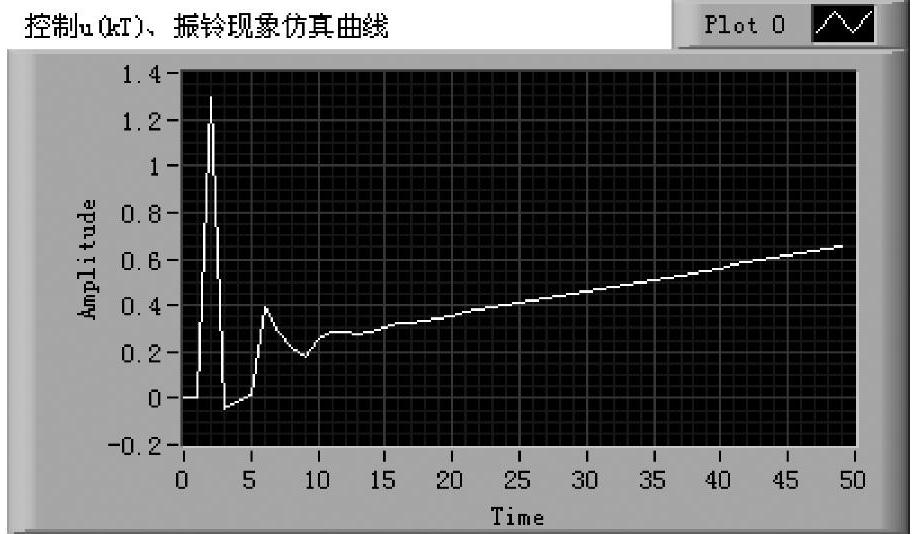
图6-6-7 消除全部振铃极点的u（kT）