数字PID调节器的设计仿真实例探析

【例6-12】数字PID调节器的设计仿真分析仪。

数字PID调节器的设计仿真分析仪程序如shixz06_12所示。前面板和程序框图面板分别如图6-5-2和图6-5-3所示。

图6-5-2 程序shixz06_12前面板

（1）离散化被控对象程序段

前面板由用户设定连续被控对象的传递函数，带零阶保持器离散化的程序段如下：

图6-5-3 程序shixz06_12框图面板

最后一句用于求被控对象极限。

运行后可得实例被控对象的连续（g0zp）和离散系统（构造gz1zp）

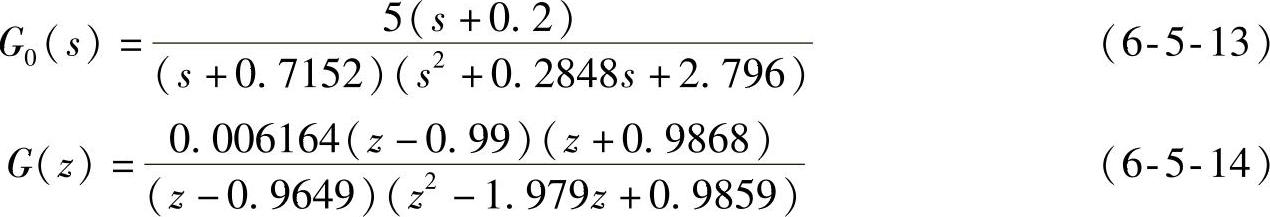
（2）取离散化被控对象极点程序段

该程序段实现6.5.2节的设计步骤（4）。

运行后得p1=0.9895-0.0826i，p2=0.9895+0.0826 i，如图6-5-4所示。

（3）计算被控对象当z=1的值G（1），求出式（6-5-9）的极限值(www.xing528.com)

运行后得到G（1）=0.5000。

（4）求出由K_p，K_D和K_I构成数字PID调节器的程序段

在MATLAB符号工具箱下求解三元一次方程组，求解K_p，K_D和K_I。

运行后，数字PID（D1_z）参数如图6-5-5所示。PID调节器为

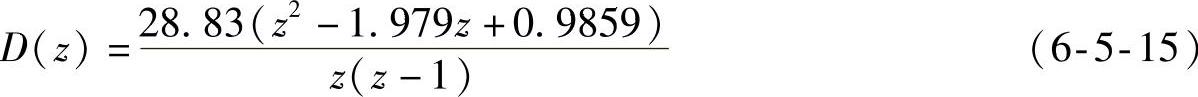
对比式（6-5-15）与式（6-5-14）的零极点相消情况。

（5）显示说明

参见图6-5-2，两个示波器屏幕分别显示恒速响应（含输入）和单位阶跃响应。前面板使用数组簇给出调节器零点和被控对象极点。实例被控对象是3阶，有3个极点，使用数组索引可以查看全部极点。PID调节器的两个零点都已显示，如图6-5-4所示。图6-5-5示出了后向差分调节器的参数。

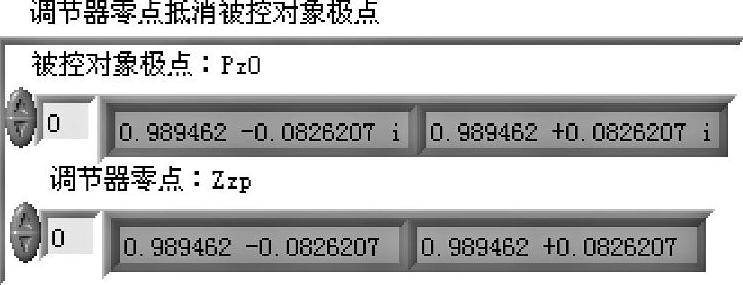
图6-5-4 调节器与被控对象的零极点对消

如果使用式（6-5-12）求解数字调节器D（z）的参数，程序如shixz06_12a所示。与shixz06_12十分相似，对同样的被控对象获得的PID参数只有K_p有些差别，如图6-5-6所示。

图6-5-5 数字PID的参数（积分取后向差分）

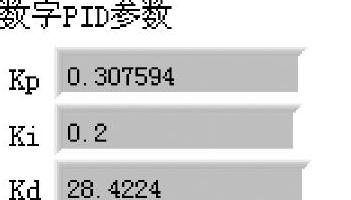
图6-5-6 数字PID的参数（积分取双线性变换）