模拟PID校正仿真分析实例优化

下面讨论两种PID校正仿真分析仪，即常规PID调节器解析设计仿真仪和改进型PID调节器图形设计仿真仪。

1.常规PID调节器解析设计仿真仪

【例6-10】常规PID调节器解析设计仿真分析仪。

使用解析方法设计常规PID调节器的仿真仪程序如shixz06_10所示。程序框图面板和前面板分别如图6-4-1和图6-4-2所示。

程序说明：

主要程序段是求解PID调节器的3个系数，即K_i，K_p和K_d。

（1）计算积分系数K_i的程序段

由式（6-4-7），计算积分系数K_i主要包括判断原待校正系统的型次及计算极限两部分。设待校正系统为最小相位系统，程序段如下：

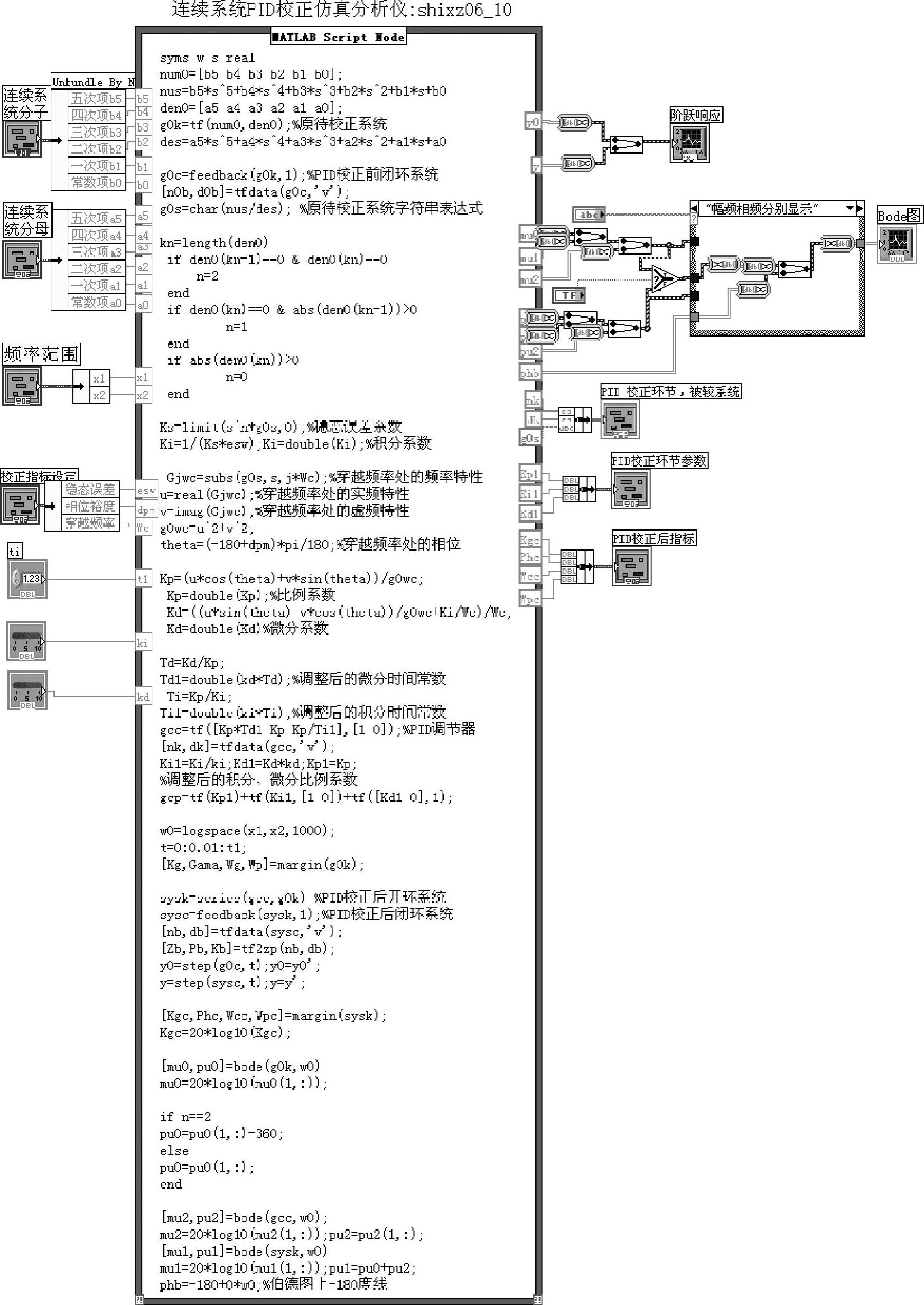
图6-4-1 程序shixz06_10框图面板

图6-4-2 程序shixz06_10前面板

程序段通过查看待校正系统分母的常数项和一次项是否为0来判断其型次：当常数项和一次项均为0时，原系统为Ⅱ型（n=2）；当仅有常数项为0时，原系统为Ⅰ型；当常数项不为0时，原系统为0型。

极限计算语句“Ks=limit（s^n*g0s，0）”中的“g0s”，必须使用符号工具箱，参见图6-4-1。

（2）计算比例系数K_p和微分系数K_d的程序段

本段程序完成式（6-4-9）～式（6-4-15）的计算。语句命令如下：

（3）积分时间常数T_i和微分时间常数T_d的计算及其调整

本仿真仪在计算出积分时间常数T_i和微分时间常数T_d之后，利用前面板的控制节点对其进行调整，可以方便地研究PID调节器中，积分环节和微分环节对校正结果的影响。

程序中，前面板上的积分修正系数k_i＞0，k_i越大，积分功能越弱。微分修正系数k_d不小于0，当取k_d=0时，微分环节不起作用，PID校正退化成PI校正。

请注意，最后进入PID调节器的各参数都是经过修正以后的参数。式（6-4-2）和式（6-4-3）的各种表达形式都是等价的，例如程序中的gcc和gcp完全相同。

（4）修正T_i，T_d对校正结果的影响

解析方法设计PID调节器可以完全满足规定的设计指标，参见图6-4-2，在不对T_i，T_d修正（k_i=k_d=1）时，校正后的相位裕度和幅值穿越频率与规定指标完全相同，但是校正后的单位阶跃响应曲线并不理想。通过使用前面板的控制节点连续改变修正系数k_d和k_i，对T_i，T_d进行修正，可以进一步提高系统的动态性能，如图6-4-3所示。

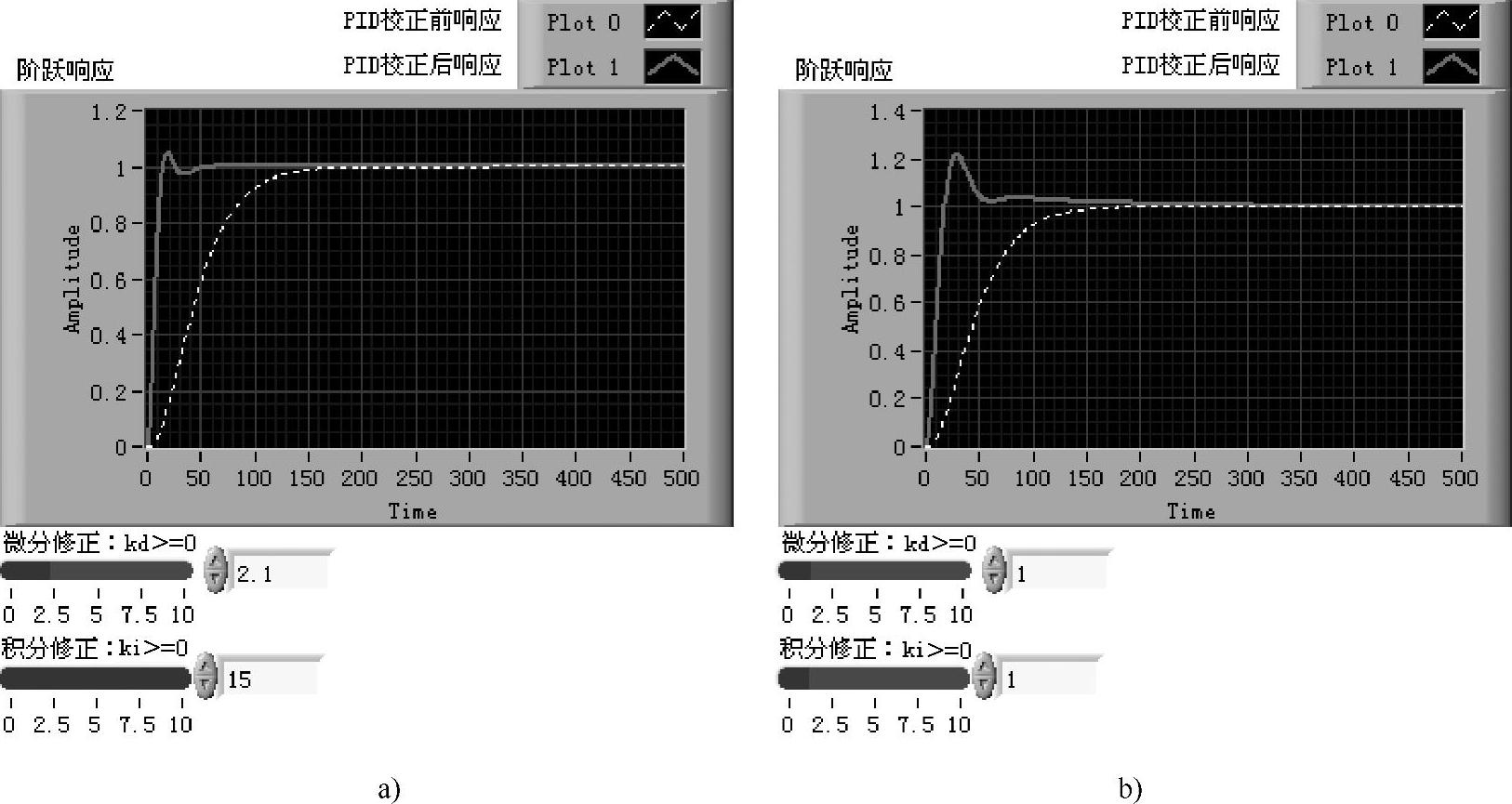
图6-4- 3修正T_i，T_d对动态特性的影响

a）对T_i，T_d进行修正 b）不对T_i，T_d进行修正

修正后系统的超调明显下降，快速性明显提高。

分析一下T_i，T_d修正前后系统闭环极点的分布，研究一下系统动态性能提高的机理。

修正前（k_i=k_d=1），仿真实例的各传递函数如下：

PID调节器（gcc）

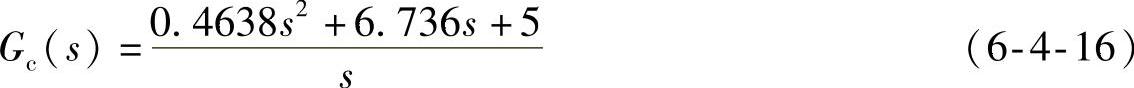
校正后开环系统（sysk）

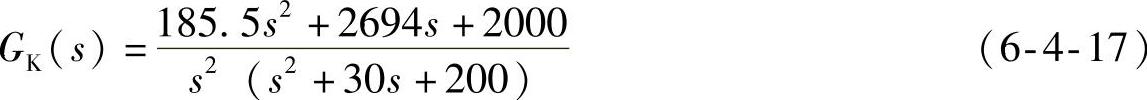
校正后为Ⅱ型系统，恒加速稳态误差为设计指标0.1，恒速输入和阶跃输入时为无差系统。

校正后闭环系统

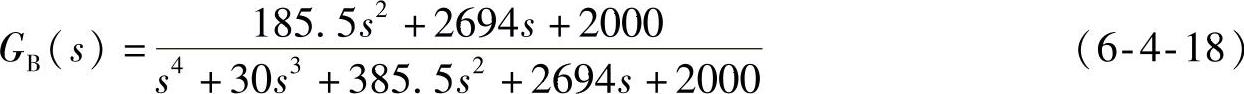
闭环零极点分布

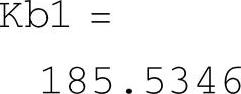
闭环零点完全由PID调节器的零点贡献。最靠近的零极点分别为-0.7847和-0.8359，相差约6%，不能进行零极点对消。

修正后（k_i=15，k_d=2.1），同一待校正仿真实例的各传递函数如下：

PID调节器

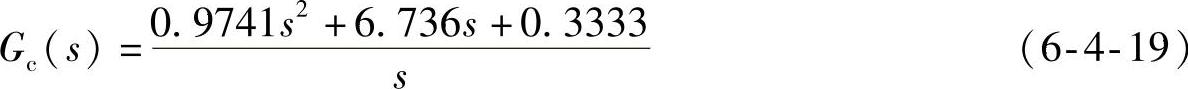
校正后开环系统

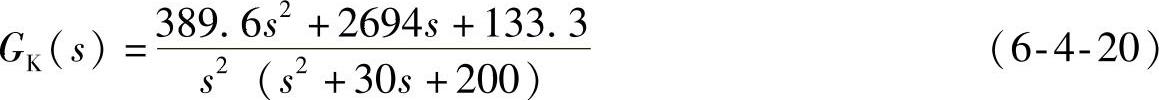
校正后闭环系统

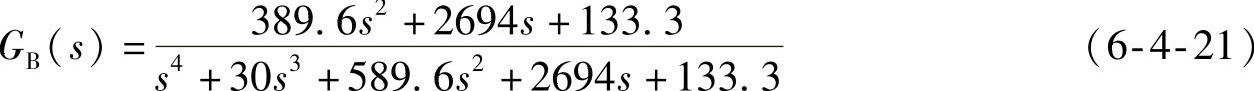
闭环零极点分布

最靠近的零极点分别为-0.0498和-0.0500，二者相差约0.4%，可以进行零极点对消。对消后的闭环传递函数为

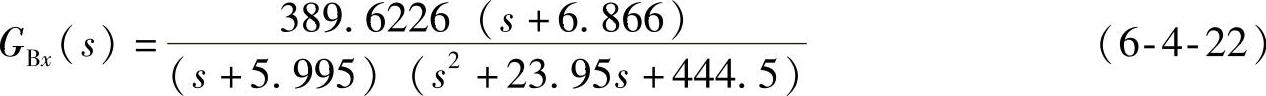
系统由4阶降成3阶。修正前后的相对稳定性指标如图6-4-4所示。相位裕度由50°提高到63.3604°，幅值穿越频率由10rad/s提高到14.3883rad/s，致使系统快速性和超调都有较大改善。

（5）关于Ⅱ型系统PID校正仿真的一些讨论

对Ⅱ型系统进行PID校正，获得的开环传递函数将含有3个积分环节，其伯德图相频曲线起始相位为-270°，在整个仿真频段可能只对-180°线相交一次（正穿越），因而出现两个特点。

第一，按照以往程序绘制伯德图，其相频曲线可能出现起始于正90°的问题，这是由于反正切函数主值限制所致。当使用以往的伯德图绘制程序（例如图6-3-10）对Ⅱ型系统

进行PID校正时，在其余参数不变的情况下，伯德图将如图6-4-5所示。系统式（6-4-23）和PID校正后系统（sysk）的相频曲线（plot3和plot4）分别起始于180°和90°，未能反映相频滞后的特征。

图6-4-4 修正T_i，T_d对相对稳定性的影响

a）对T_i，T_d进行修正 b）不对T_i，T_d进行修正

为了避免这种情况，本仿真仪伯德图绘制程序添加了型次判断功能块：

经过修改后，在同样条件下，系统式（6-4-23）校正前后的伯德图如图6-4-6所示。

在上述程序中，对Ⅱ型系统的相频数据使用减去360°的计算方法，同时，对于PID与原系统串联后的相频数据使用二者相频数据相加的计算方法。

第二，可能造成幅值裕度为负值，但系统却是稳定的矛盾情况，这方面请读者参考有关论著。不同的学者，对于稳定性的伯德判据尚有不同论述^[12]。

对系统式（6-4-23）进行常规PID校正后的前面板如图6-4-7所示。

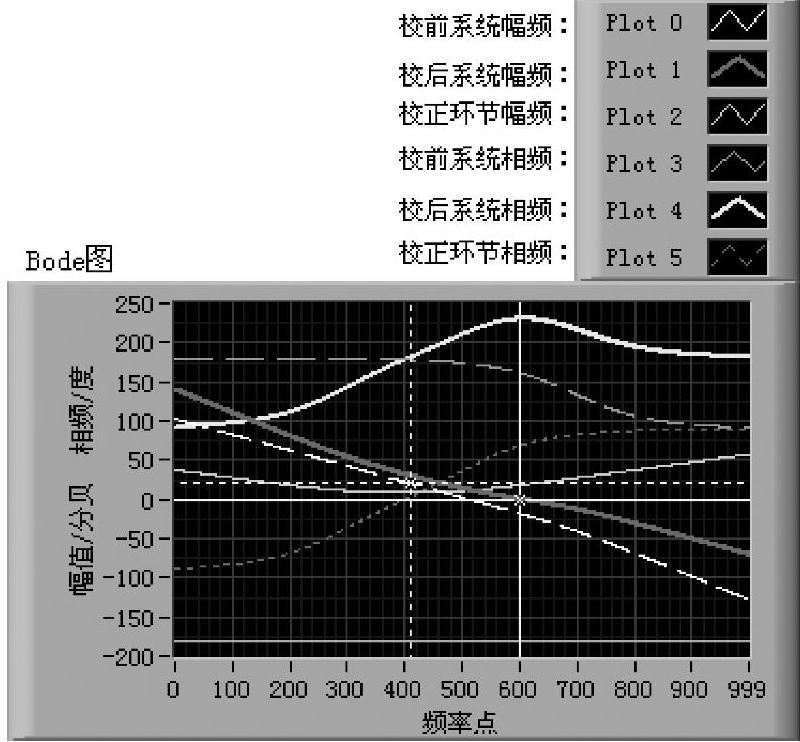
图6-4-5 不正确的Ⅱ型系统相频曲线图

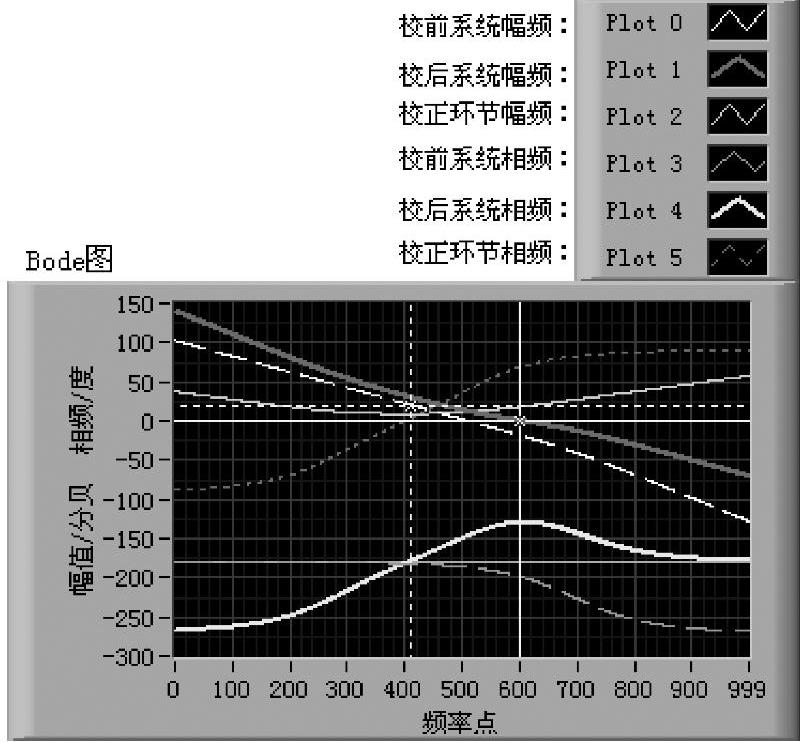
图6-4-6 正确的Ⅱ型系统相频曲线图

由图可见，系统式（6-4-23）经PID校正后，示出的幅值裕度为-30.47dB，参见图6-4-7“Bode图”中实线坐标系（cursor1）所示。这是使用命令margin（sysk）获得的，这表明命令“margin”所获得的结果判断系统稳定性有时会出现偏差。

分析图6-4-7的各传递函数，可以证明该系统校正前不稳定，经PID校正后系统稳定。

PID校正环节（gcc）

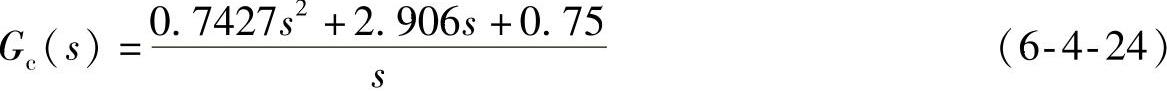
PID校正后系统开环传递函数（sysk）

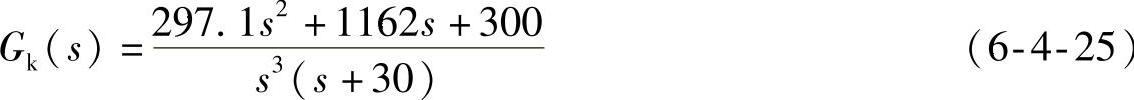
校正后开环系统为Ⅲ型。

PID校正后系统闭环传递函数

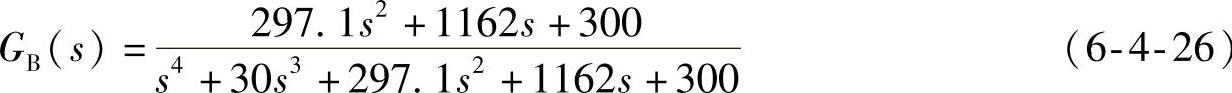
PID校正后系统闭环零极点分布为

闭环极点全部处于复平面左边，而且具有零极点相消的条件。

图6-4-7 对系统式（6-4-23）的PID校正前面板

2.改进型PID校正设计仿真仪^[13]

例6-10通过解析方法得到常规PID调节器的设计参数。在工程实用中，这种PID调节器有一定的局限，常常需要进行改进。下面介绍一种改进型PID校正设计仿真仪，并且利用虚拟仪器面板上的控件功能，直接使用仿真结果研究调节器参数对校正结果的影响，借助于图形方法，在获得优良控制效果的基础上获得改进PID调节器的参数。

设反馈控制系统框图如图6-4-8所示，图中G_c（s）采用图6-4-9不完全微分的改进型PID调节器。引入低通滤波器改进理想微分器，可以更好地抑制高频干扰，减弱对噪声的放大。

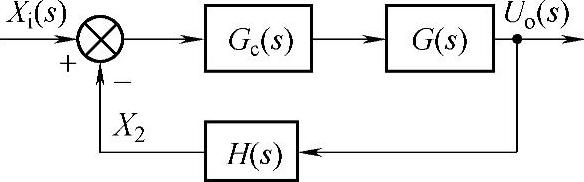
图6-4-8 反馈控制系统框图

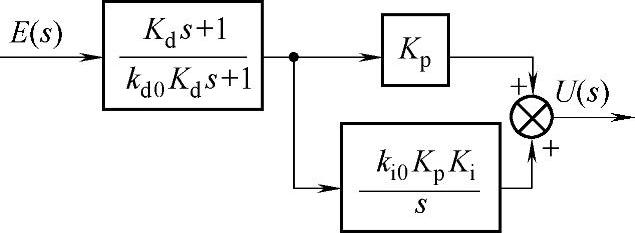
图6-4-9 改进型PID调节器框图

改进型PID调节器（图6-4-9）的传递函数为(www.xing528.com)

式中，K_p为比例系数；K_d为微分时间常数；K_i为积分时间常数的倒数；k_d0是调节低通滤波器时间常数的系数；k_i0为控制积分环节的常数，k_i0=1表示投入积分环节，k_i0=0表示切除积分。

通过参数选择与调整，式（6-4-27）（图6-4-9）可以构成多功能校正环节。其中包括不实施校正，采用P、PI、PD或PID等校正方法实施校正，简述如下：

1）当K_p=1，k_d0=1，k_i0=0时，式（6-4-27）为

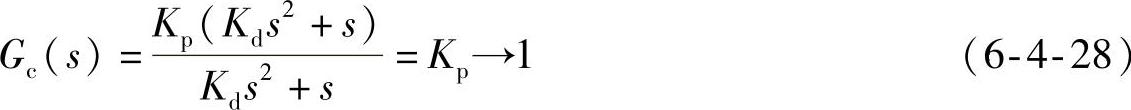
比例、积分和微分环节均不投入。校正环节出现两对零极点对消，不起校正作用，便于研究被控对象校正前的特性。如果此时K_p不等于1，校正环节成为单一的比例（P）环节。

2）当k_i0=0，K_p和k_d0可调且不为1时，式（6-4-27）为

校正环节对消了原点处的零极点，成为带低通滤波器的比例微分（PD）调节器。调节K_p可以改变增益，调节k_d0和K_d，特别是k_d0，可以改变PD调节器的频率特性，从而改变其校正功能。为使PD调节器具有超前校正功能，应当使k_d0在区间（0，1）之间可调。

3）当k_d0=1，k_i0=1，K_p可调，式（6-4-27）为

在对消了（-1/K_d）处的零极点之后，校正环节成为比例积分（PI）调节器。

4）当k_i0=1，k_d0≠1，K_p可调且不为1时，式（6-4-27）为

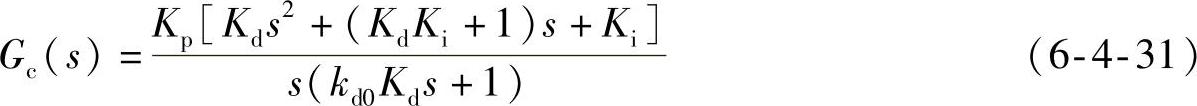
校正环节还原成完整的PID调节器，可调参数为4个。

改进型PID校正设计、仿真仪见例6-11。

【例6-11】采用不完全微分的改进型PID校正设计、仿真仪^[13]。

不完全微分PID校正设计、仿真仪程序如shixz06_11所示。程序框图面板和前面板分别如图6-4-10和图6-4-11所示。

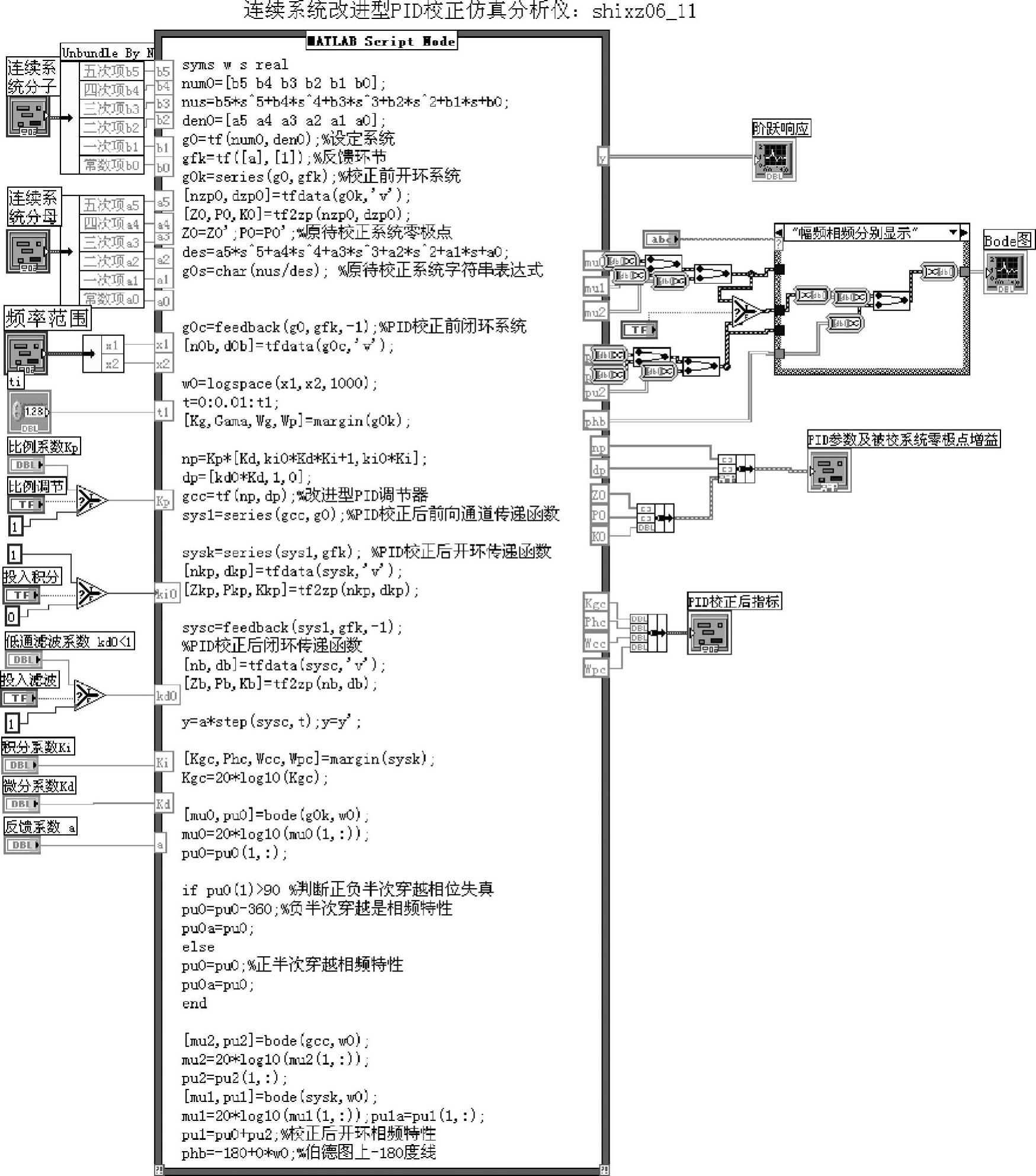
图6-4-10 程序shixz06_11框图面板

程序说明：

（1）PID调节器几种算法的切换

本仿真仪的主要特点是PID调节器的参数通过前面板的对应控件调节设定，主要控件包括3个选择开关和4个可调参数滑竿，参见图6-4-12。选择开关在程序面板中的输入接口如图6-4-13所示。

图6-4-11 程序shixz06_11前面板

图6-4-12中“比例调节，投入积分，投入滤波”3只开关有接通和断开两种状态，当开关上的小绿灯点亮时表接通，熄灭时表断开。

完整的PID校正：3只开关均接通。“投入积分”使k_i0=1，“比例调节”和“投入滤波”分别使比例系数K_p和低通滤波系数k_d0可调。

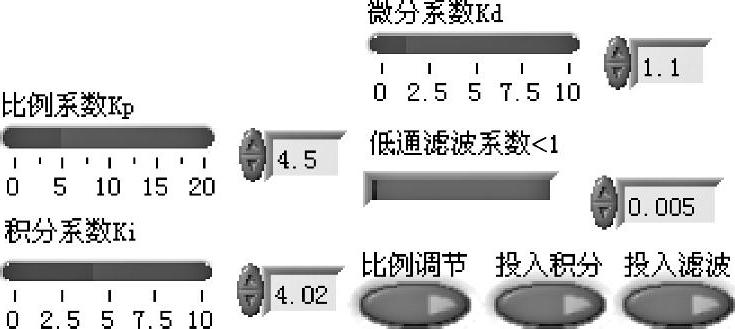
图6-4-12 PID校正方式及参数调节控件

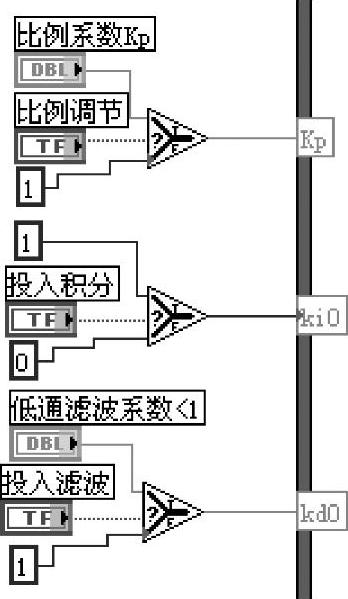
图6-4-13 选择开关的输入接口

PI校正：“投入滤波”开关断开，使k_d0=1，低通滤波系数不可调；“比例调节，投入积分”两只开关接通，使k_i0=1，构成式（6-4-30）的PI调节器。

PD校正：“投入积分”开关断开，使k_i0=0，积分环节不起作用；“比例调节，投入滤波”两只开关接通，使K_p，k_d0和K_d可调，构成如式（6-4-29）的PD调节器。

（2）部分语句说明

改进型PID传递函数、校正后系统开环传递函数和系统闭环传递函数的构成语句如下：

由于系统反馈环节（gfk）可以设定，开环传递函数与前向通道传递函数不一定相等，语句中sys1表示前向通道传递函数，sysk表示开环系统传递函数（参见图6-4-8）。

程序还给出了待校正系统、前向通道传递函数和开环传递函数的零极点增益模型，以便判断最小相位系统与非最小相位系统。

仿真发现，对于Ⅱ型系统中的负半次穿越，MATLAB命令所绘制的伯德图的纵坐标表达为相位超前（示数为正）。设Ⅱ型系统的频率特性为

当系统中T₁＜T₂，导前环节的转角频率大于惯性环节的转角频率（ω_c1=1/T₁＞ω_c2=1/T₂）时，惯性环节相位滞后作用先于导前环节相位超前作用，总体效果滞后。对数相频曲线起始于-180^o，并且构成负半次穿越。以T₁=5，T₂=10为例有

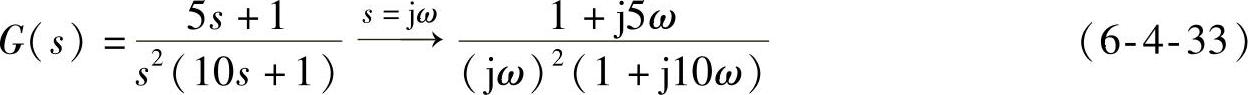
对系统（6-4-33）使用命令bode所编写的相频特性曲线语句为

得到对数相频特性曲线如图6-4-14所示。曲线纵坐标示数为正相位，不能真实反映式（6-4-33）

总体的相位滞后和起始负半次穿越的相频特性。

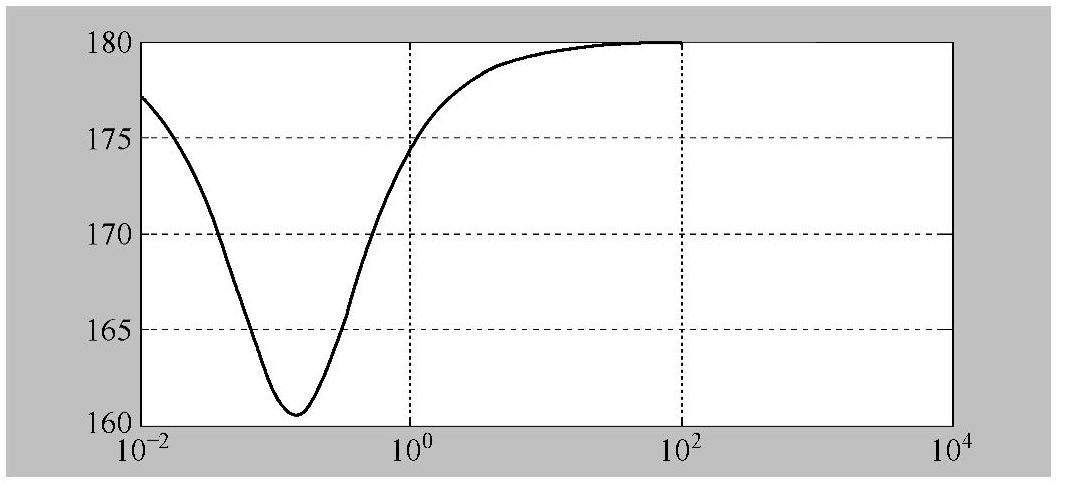
图6-4-14 bode命令未能正确反映Ⅱ型系统式（6-4-33）相频特性

本仿真仪对此段程序进行如下修改：

将系统式（6-4-33）输入仿真仪shixz06_11，运行后得到如图6-4-15所示的对数相频特性曲线，能够正确反映滞后和负半次穿越的特征。

（3）仿真实例的传递函数

校正前的系统开环传递函数（g0k）

校正前的系统闭环传递函数（g0c）

注意反馈系数为2。

改进型PID调节器（gcc）

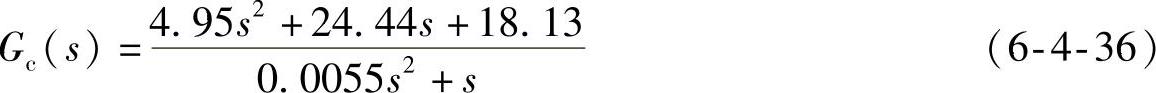
校正后系统开环传递函数（sysk）

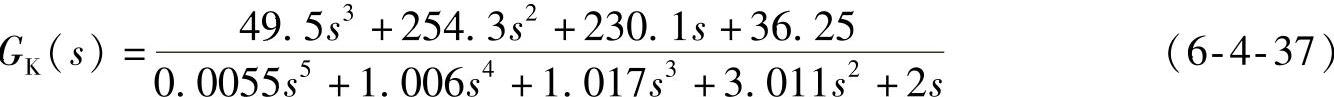
采用幅频、相频分别显示方式校正前系统，PID校正环节和校正后开环系统的相频曲线如图6-4-16。

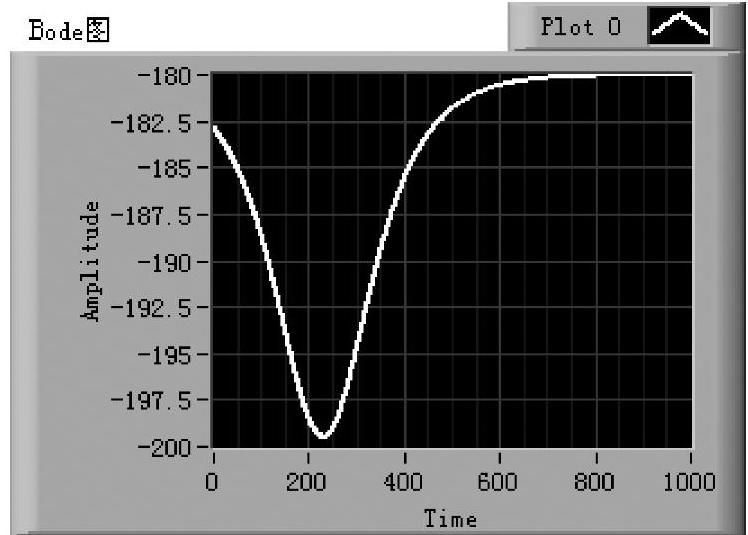
图6-4-15 Ⅱ型系统式（6-4-33）的负半次穿越相频特性曲线

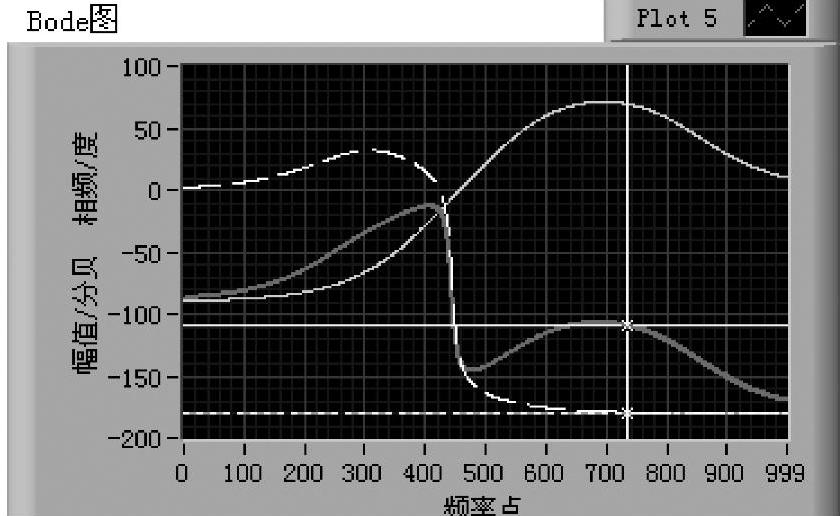
图6-4-16 PID校正环节和校正后开环系统的相频曲线

图中虚线为校正前系统式（6-4-34）相频特性曲线，PID校正环节显示出滞后超前相频特性，校正后开环系统式（6-4-35）相频特性起始于-90°，终止于-180°。

校正后系统闭环传递函数（sysc）

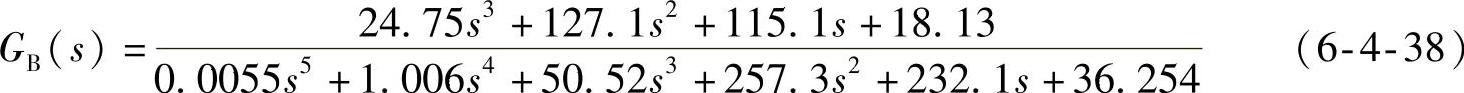
作为对比，图6-4-17给出图6-4-11仿真实例校正前后系统的单位阶跃效应曲线。

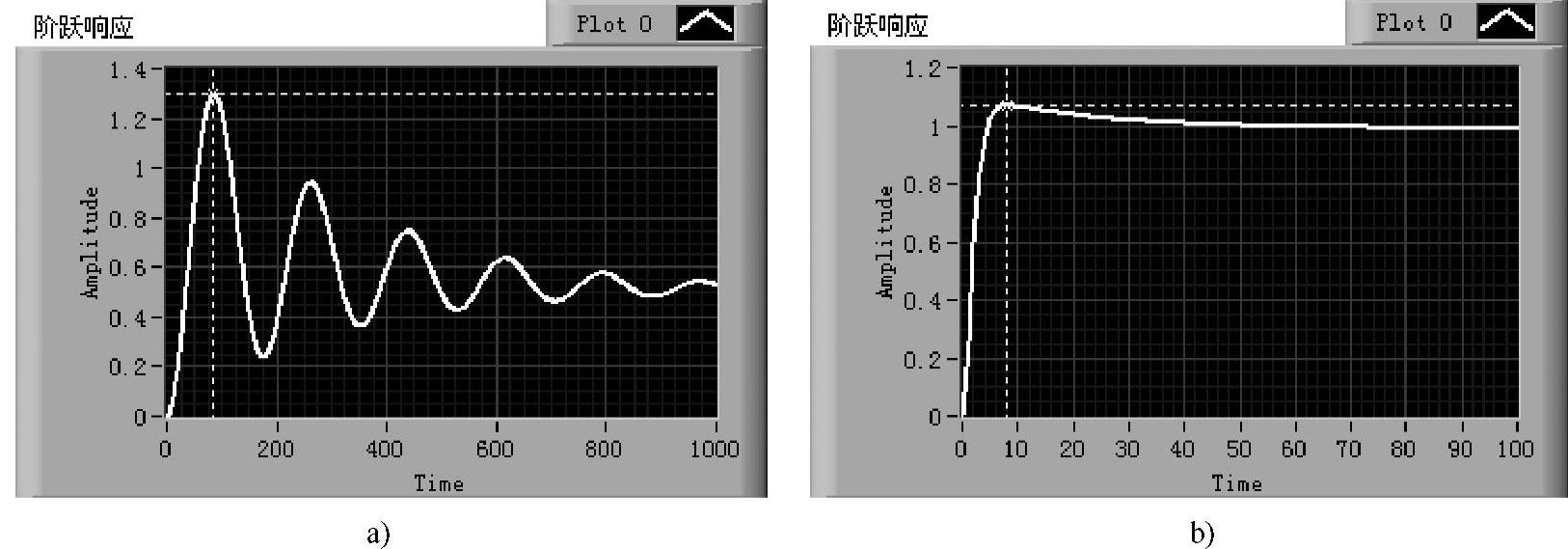
图6-4-17 校正前后单位阶跃效应曲线对比

a）校正前 b）校正后

（4）仿真结果的显示与直接测量

仿真仪前面板上提供的数字显示器可以直接显示仿真结果，也可以使用前面板上示波器内的测量坐标对仿真结果进行测量，参见图6-4-11。

PID调节器参数和待校系统零极点增益数字显示器簇如图6-4-18所示。

图6-4-18 PID调节器参数和待校系统零极点增益数字显示器簇

PID算法与式（6-4-31）一致。根据使用者在前面板上选择调整的参数，参数由算法式（6-4-31）决定。

“待校系统的零极点增益”显示的是校正前系统开环传递函数（g0k）（式6-4-34）的数据（参见图6-4-8）。注意图6-4-18中极点只显示了一个数值，其余两个极点可以通过改变簇的数组索引得到。

由坐标系测量校正后系统时域性能指标如下：峰值时间为0.08s，超调约为7%，当规定误差带为±5%时，调整时间为0.16s。可见，校正后系统时域性能有很大提高。

由坐标系测量部分频域性能指标如下：将图6-4-11的幅值穿越频率代入起始和终止频率点，幅频曲线穿越0dB线的频率点736，得

相位裕度γ=180°-109.77°=70.23°，结果和数字指示器之间的误差在允许范围之内。

作为对比，此处研究一个非最小相位系统的仿真结果。

在仿真仪上输入原始开环系统

得到系统对数相频特性曲线如图6-4-19所示，待校正系统零极点增益如图6-4-20所示。

分别对比图6-4-19与图6-4-16，图6-4-20与图6-4-18，由于非最小相位系统式（6-4-39）有一对正实部共轭极点，因此总体相位超前。

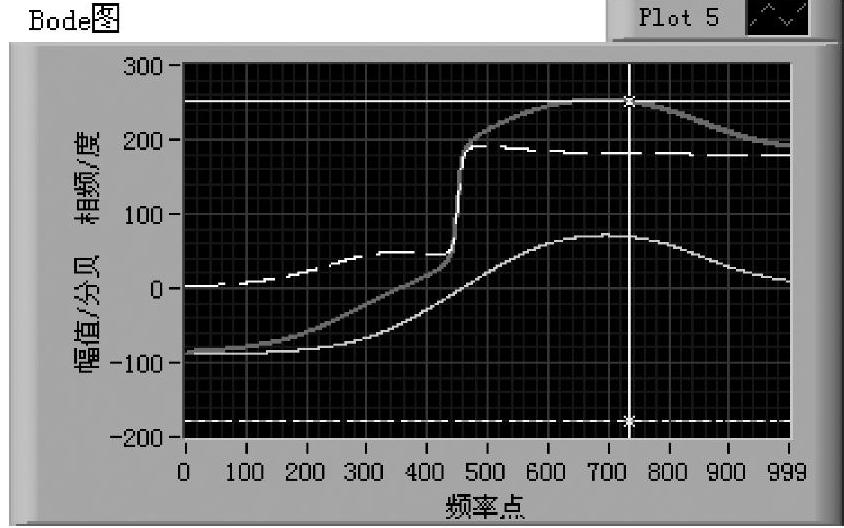
图6-4-19 非最小相位系统的相频特性曲线

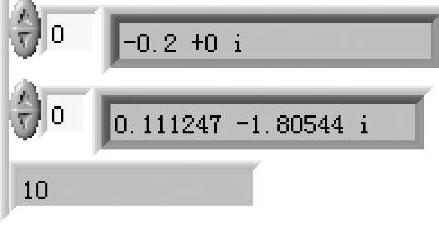
图6-4-20 非最小相位系统的零极点增益