如何解决2.0型系统的滞后—超前问题？

（1）满足稳态恒速误差要求的0型系统的滞后—超前校正

【例6-8】满足稳态恒速误差要求的0型系统滞后—超前校正仿真分析仪。

满足稳态恒速误差要求的0型系统滞后—超前校正程序如shixz06_08所示。程序框图面板和前面板分别如图6-3-7和图6-3-8所示。

程序说明：

如前所述，给出稳态恒速误差的0型待校正系统，需要校正环节含有积分因子。为了方便，可将校正环节内的积分因子纳入待校正系统之中，使问题仍然归于Ⅰ型系统的滞后—超前校正。除了将待校正系统变为Ⅰ型系统之外，其余程序与例6-7相同，只是校正后系统比待校正系统高出了二阶。

实例的原0型系统（g0）为

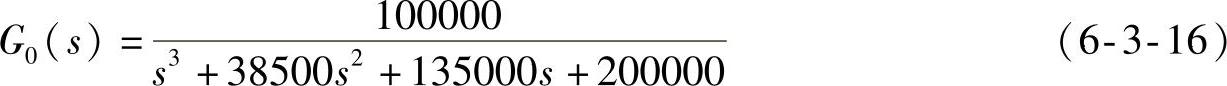
考虑恒速误差指标后的实际被校正系统（g0k1）为

显然，待校正系统由3阶变成了4阶，由0型变成了Ⅰ型。系统的稳态恒速误差由无穷大变为e_vs=1/100=0.01。当然，如果不加校正，式（6-3-17）所对应的闭环系统是不稳定的。

滞后校正环节（gc2）为

式中，β=65.4997；ω_gcn=1.3612.实例取k_T=5.6，T₂=k_T/ω_gcn=4.114s。

超前校正环节（gc1）为

其中，选取k_cg=0.1，T₁=k_cg*T₂=0.4114s。

滞后—超前校正环节（gcc）为

滞后校正后的开环系统（sysk2）为

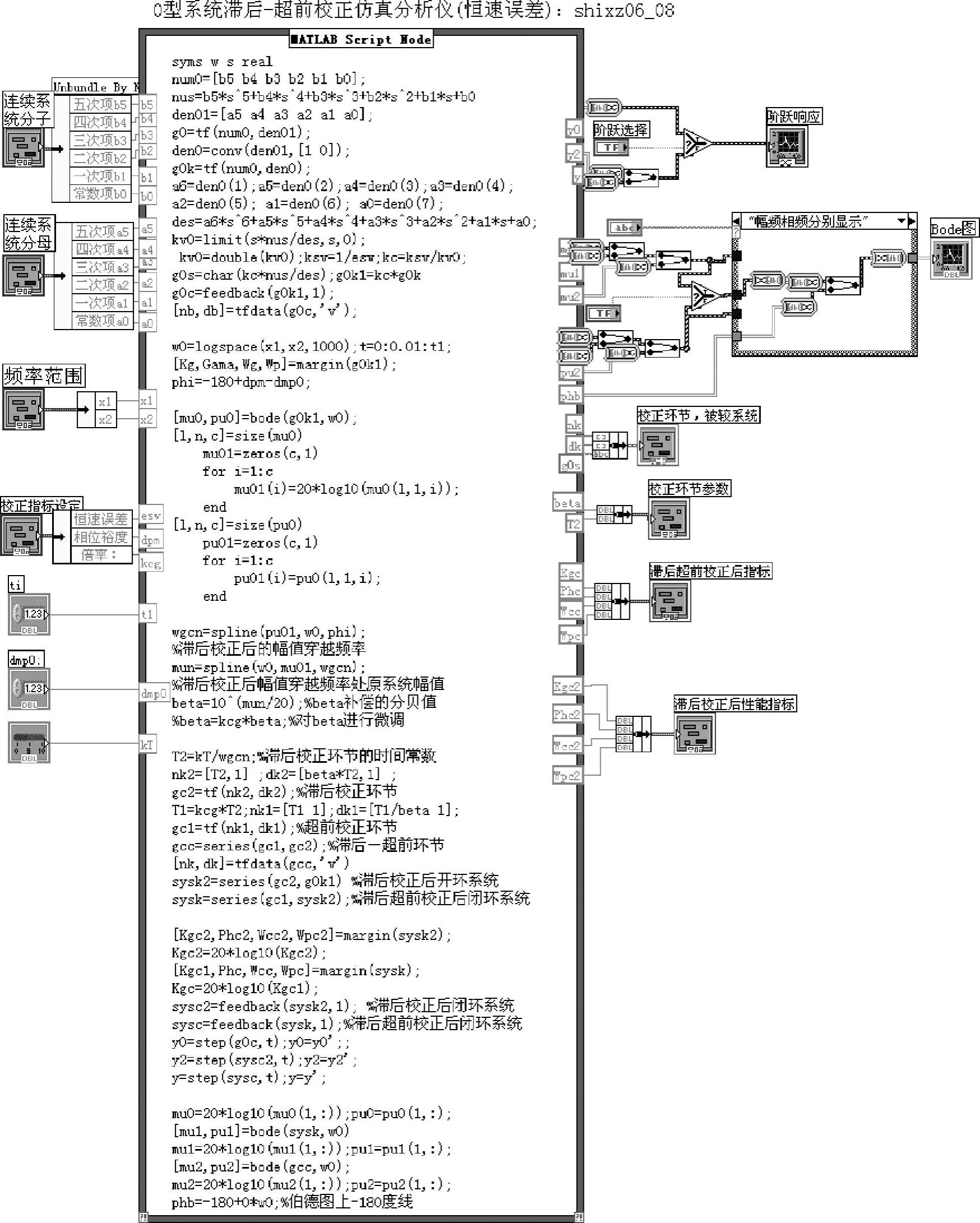
图6-3-7 程序shixz06_08框图面板

图6-3-8 程序shixz06_08前面板

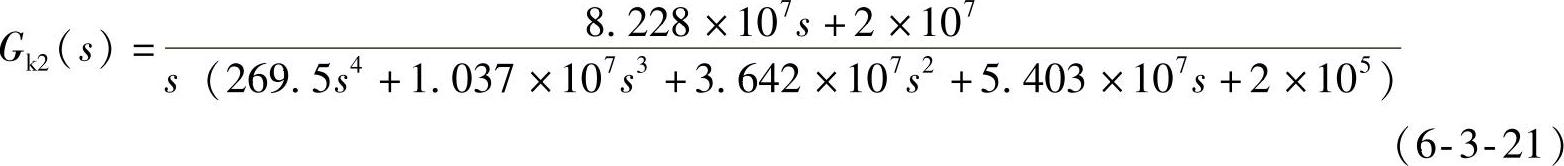
滞后校正后的闭环系统（sysc2）为

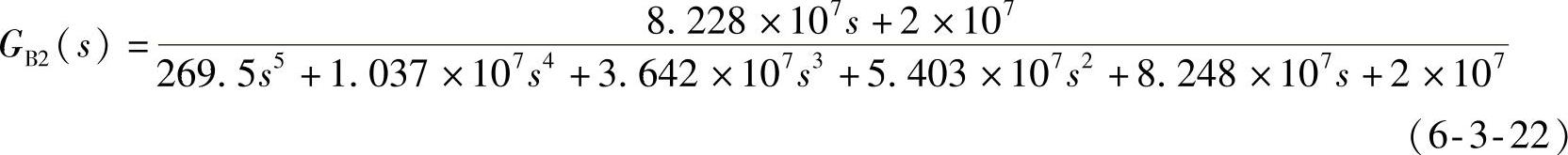
滞后校正后的频域相对稳定性指标重新示于图6-3-9中。数据表明，进行滞后校正后其幅值穿越频率（1.37709rad/s）已经小于相位穿越频率（2.08703rad/s），系统已经由不稳定变成稳定。但幅值裕度仅为5.68997dB，相位裕度仅为24.4808°，不满足设计指标要求，由其单位阶跃响应曲线可见系统动态特性较差，还需进行超前校正。

图6-3-9 滞后校正系统的相对稳定性指标数据

滞后—超前校正后的开环系统（sysk）为

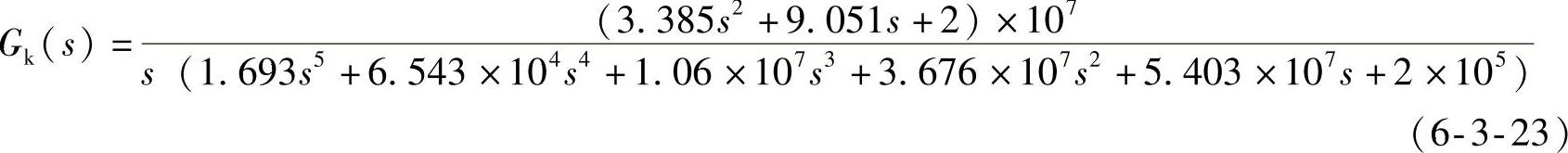
滞后—超前校正后的闭环系统（sysc）为

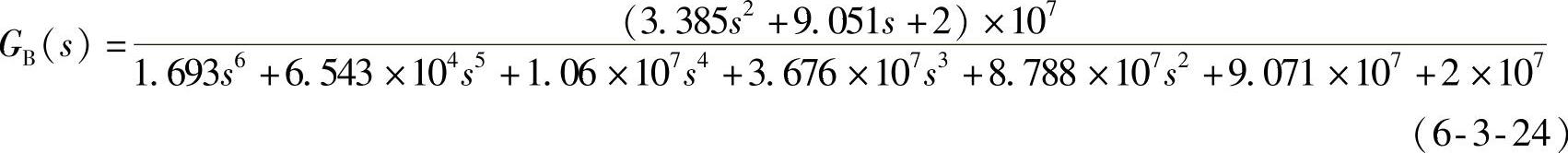
在滞后校正基础上再进行超前校正，构成完整的滞后—超前校正后，系统相对稳定性指标重新示于图6-3-10中。和图6-3-9所示数据相比，有很大改善，幅值裕度增加到32.6988dB，相位裕度增加到50.2508°，动态性能有较大改善，参见图6-3-11中的两条阶跃响应曲线。

图6-3-10 例6-8滞后超前校正后频域性能

图6-3-11 例6-8滞后校正和滞后超前校正动态性能比较

（2）满足稳态位置误差的0型系统的滞后—超前校正

【例6-9】满足稳态位置误差要求的0型系统滞后—超前校正仿真仪。(www.xing528.com)

满足稳态位置误差要求的0型系统滞后—超前校正仿真仪程序如shixz06_09所示。程序框图面板和前面板分别如图6-3-12和图6-3-13所示。

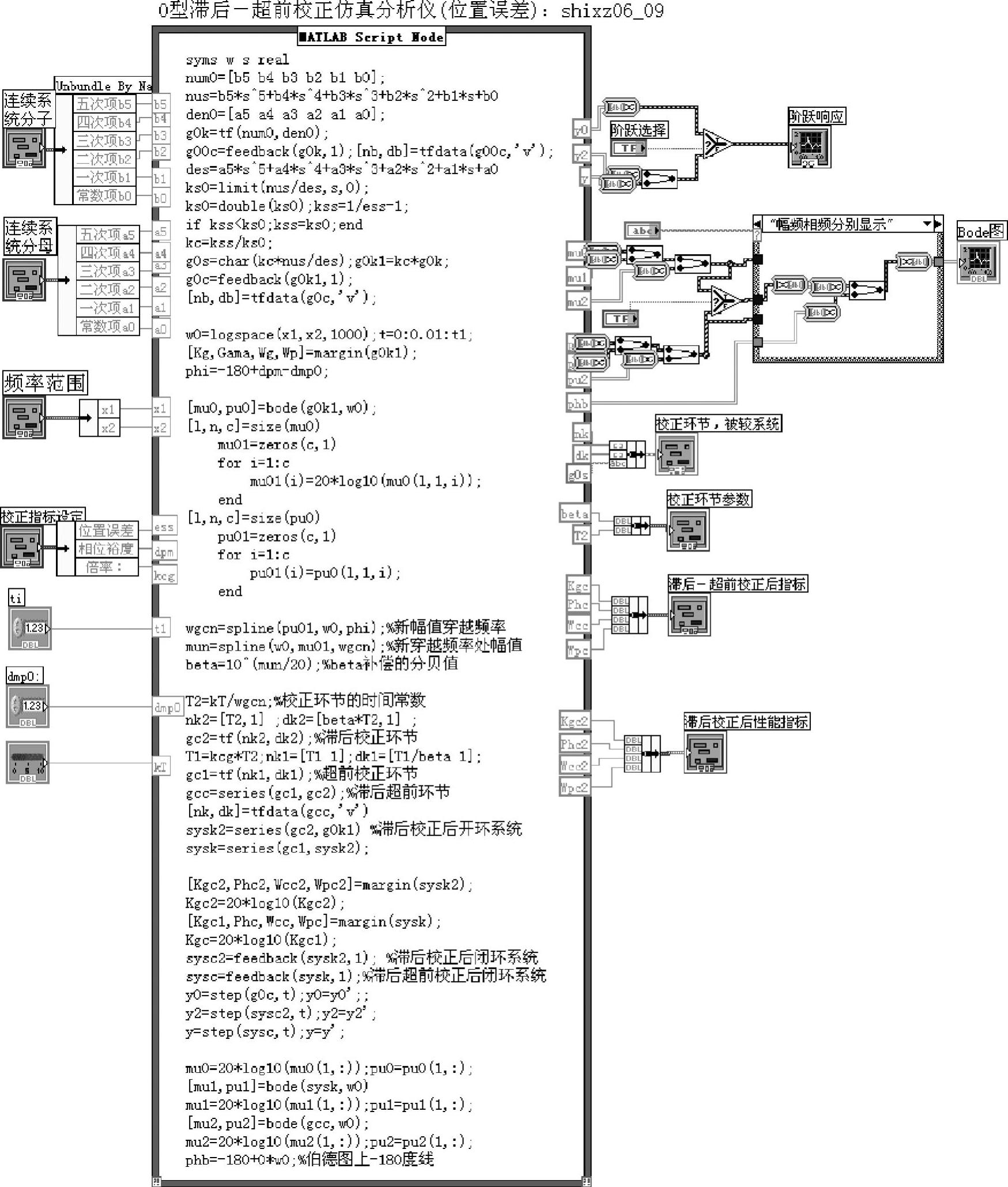
图6-3-12 程序shixz06_09框图面板

图6-3-13 程序shixz06_09前面板

程序说明：

满足校正后稳态位置误差的程序段说明见例6-3，滞后—超前校正部分的程序见例6-7，仿真实例模型如下：

原始待校正0型系统（g0k）为

显然，系统稳态位置误差为1/（1+1）=0.5，不满足设计要求。

考虑稳态位置误差指标后的实际被校正系统（g0k1）为

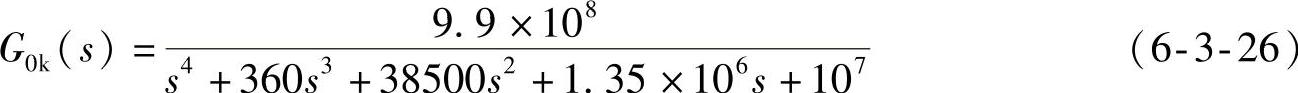
增益的提高，使得稳态位置误差变为1/（99+1）=0.01，满足设计指标要求。当然，如果不加校正，式（6-3-26）所对应的闭环系统是不稳定的。

滞后校正环节（gc2）为

式中，β=18.4426；ω_gcn=37.9701。实例取k_T=6，T₂=k_T/ω_gcn=0.158s。

超前校正环节（gc1）为

其中，选取k_cg=0.1，T₁=k_cg*T₂=0.0158s。

滞后—超前校正环节（gcc）为

滞后校正后的开环系统（sysk2）为

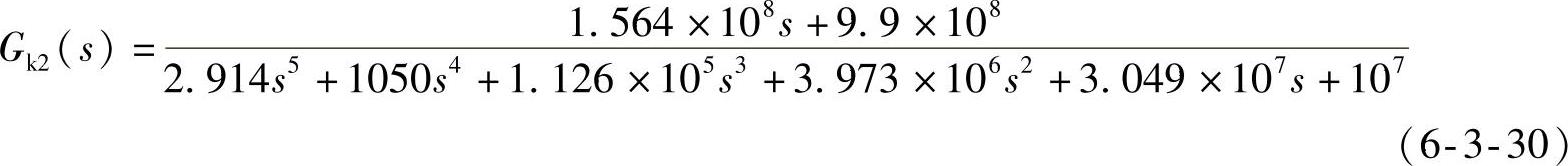
滞后校正后的稳态位置误差与式（6-3-26）相同。此时系统已经稳定，可以计算稳态误差。

滞后校正后的闭环系统（sysc2）为

滞后校正后的频域相对稳定性指标重新示于图6-3-14中。数据表明，进行滞后校正后其幅值穿越频率（38.3176rad/s）已经小于相位穿越频率（56.6957rad/s），系统已经由不稳定变成稳定。但幅值裕度仅为5.69066dB，相位裕度仅为26.4854°，不满足设计指标要求，由其单位阶跃响应曲线可见系统动态特性较差，还需进行超前校正。

图6-3-14 例6-9滞后校正后系统的相对稳定性数据

滞后—超前校正后的开环系统（sysk）为

滞后—超前校正后的闭环系统（sysc）为

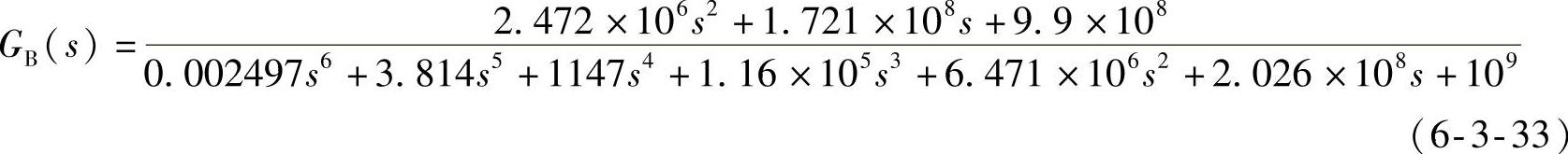
在滞后校正基础上再进行超前校正，构成完整的滞后—超前校正后，系统相对稳定性指标重新示于图6-3-15中。和图6-3-14所示数据相比，有很大改善，幅值裕度增加到13.8479dB，相位裕度增加到50.8188°，动态性能有较大改善，参见图6-3-16中的两条阶跃响应曲线。

图6-3-15 例6-9滞后超前校正后频域性能

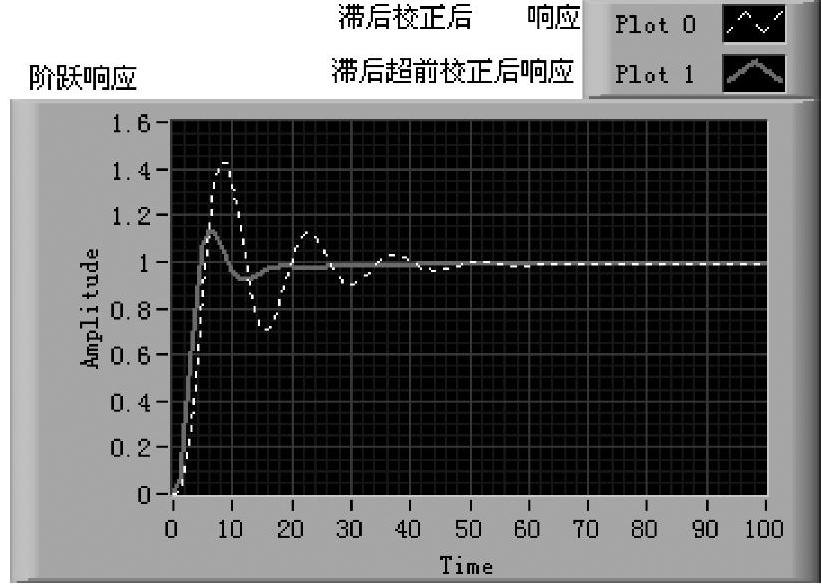
图6-3-16 例6-9滞后校正和滞后超前校正动态性能比较