频域和时域性能指标的关系

时间：2023-07-02 理论教育版权反馈

【摘要】：前已述及，系统性能指标可以分成时域性能指标和频域性能指标两类，频域性能指标中又可分为开环频域性能指标和闭环频域性能指标，这三种性能指标之间是相互联系的。对于二阶系统，系统开环相位裕度γ与闭环频率特性谐振峰值Mr和单位阶跃响应的最大超调Mp之间存在确定的关系。在该范围内，相位裕度与超调呈较好的线性关系。

频域和时域性能指标的关系

前已述及，系统性能指标可以分成时域性能指标和频域性能指标两类，频域性能指标中又可分为开环频域性能指标和闭环频域性能指标，这三种性能指标之间是相互联系的。例如，如果开环相位裕度太小，表明奈奎斯特轨迹在比较靠近（-1，j0）点的地方穿越负实轴，在这个频率附近必有G_k（jω）≈1。由开闭环频率特性关系

必然有G_B（jω）＞＞1。因而在该频段内必然会出现一个谐振峰，系统出现强烈振荡现象，系统超调随之增大。下面分别进行讨论。

1.相位裕度与闭环动态性能的关系

文献[10]介绍，在一定条件下，相位裕度γ与谐振峰值M_r之间有

单位阶跃响应的最大超调M_p与相位裕度γ、谐振峰值M_r之间有经验公式

下面介绍相位裕度与谐振峰和最大超调的仿真分析。

【例5-6】相位裕度对谐振峰值和超调影响的仿真分析仪。

对于二阶系统，系统开环相位裕度γ与闭环频率特性谐振峰值M_r和单位阶跃响应的最大超调M_p之间存在确定的关系。对于三阶以上的系统，难于求出它们之间的解析关系，当然在一定条件下可以使用前述文献介绍的经验公式，但是经验公式毕竟有自己的局限性。使用计算机仿真可以根据不同系统，在一个比较大的范围内比较准确地描述相位裕度、谐振峰值和超调之间的数量关系，这对工程设计是很有帮助的。具有这种功能的仿真仪程序如shixz05_06所示，其程序前面板和框图面板分别如图5-2-14和图5-2-15所示。

程序说明：

1）被研究的五阶及其以下的开环系统中，分子常数项b₀可以在一定范围内变化。用户只需在“b₀分子常数项变化范围”框内设置其上下限和变化步长即可。这个范围也就是程序的仿真范围。需要注意上下限，特别是上限设置必须保持闭环稳定，不可太大。

程序使用for循环计算仿真范围内对应各个系统的相位裕度γ（程序中使用符号Pm），闭环频率特性谐振峰值M_r和单位阶跃响应的最大超调M_p。语句如下：

图5-2-14 程序shixz05_06前面板

图5-2-15 程序shixz05_06框图面板

2）仿真计算值序列存于表格“计算值”中，拟合后的函数序列存于表格“M_r拟合值”和“M_p拟合值”之中，对应曲线绘制在前面板的两个XY函数记录仪上。第一个记录仪绘制M_r～P_m曲线，第二个记录仪绘制M_p～P_m曲线。其中，“plot0”为计算值曲线，“plot1”为拟合值曲线。

3）多项式拟合。程序对所获得的计算值使用多项式拟合求出其函数关系。拟合时，选择相位裕度P_m为自变量x，闭环谐振峰值M_r和超调M_p分别为函数y₁与y₂。程序实例所得到的拟合关系为

Y₁=24.60785-0.88470x+0.Oll10x²-0.00005x³ (5-2-9)

Y₂=73.10219-1.03720x-0.00457x²+0.00007x³ (5-2-10)

拟合函数借助LabVIEW中的一般多项式拟合（General Polynomial Fit），其路径如图5-2-16所示。

图5-2-16 多项式拟合路径

一般多项式拟合节点如图5-2-17所示。

下面介绍主要输入、输出端口。

Y：被拟合的函数输入值，一维数组，其元素个数必须大于多项式阶数。

X：被拟合的自变量输入值，与Y个数相同的一维数组。

Weight：权重，默认值为1。

图5-2-17 一般多项式拟合节点

polynomial order：多项式阶数。用户在前面板“拟合多项式阶数（正整数）”框内设置为m，默认值为二阶。

algorithm：规定计算拟合值的方法，不连接时采用最小二乘法。

Best Polynomial Fit：返回拟合后的函数序列。

Polynomial Coefficients：拟合多项式系数，构成拟合多项式

mse：差方均值。

仿真表明，当相位裕度不大于60°时，相位裕度越大，谐振峰值和超调越小，呈现单调下降关系。在该范围内，相位裕度与超调呈较好的线性关系。当相位裕度超过60°后，相位裕度的增加对减小谐振峰值和超调的作用已经减弱，呈现饱和趋势。所以工程上希望相位裕度不超过60°是有道理的。

2.谐振峰值与最大超调之间的关系

以相位裕度为参变量，获得谐振峰值与最大超调之间关系的程序如shixz05_06a所示。该程序与shixz05_06主体相同，有两点区别：第一是XY函数记录仪绘制谐振峰值M_r与最大超调M_p之间的关系，如图5-2-18和图5-2-19所示。第二是多项式拟合直接采用M_r与M_p计算值进行。为便于比较，图5-2-18和图5-2-19中的纵横坐标相互交换。显然M_r与M_p之间基本上呈现单调正变关系。注意它们的饱和段。

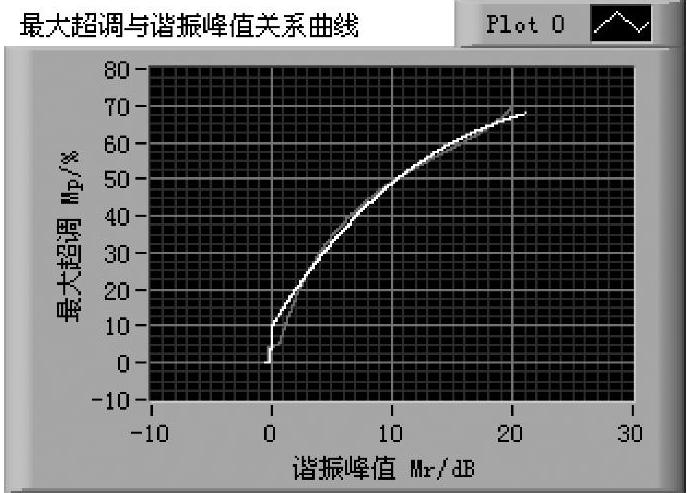
图5-2-18 最大超调与谐振峰值关系图

图5-2-19 谐振峰值与最大超调关系图

仿真时请注意，拟合曲线精度与形状和拟合步长t_b的关系极大，步长减小，拟合精度提高，但计算量迅速上升。

系统开环幅值裕度对闭环谐振峰值和单位阶跃响应的超调影响研究见例5-7。(www.xing528.com)

【例5-7】谐振峰值、最大超调和幅值裕度关系仿真分析仪。

谐振峰值、最大超调与幅值裕度关系的仿真分析如程序shixz05_07所示。其程序前面板和框图面板分别如图5-2-20和图5-2-22所示。

程序说明：

shixz05_07与shixz05_06相似。shixz05_07仿真曲线的自变量（横坐标）为幅值裕度G_m，函数分别为闭环谐振峰值M_r和最大超调M_p。拟合曲线数据采用LabVIEW的指数拟合（Exponential Fit）节点获得。指数拟合节点如图5-2-21所示。

下面介绍特殊端口含义及使用方法。

tolerance：规定内插容限值，采用最小二乘法时容限默认值为0.0001。

method：规定计算拟合值的方法，默认为最小二乘法。还可以选择Least Absolute Residual（最小绝对余差）法和Bisquare（双二次）法。程序使用一个控制开关选择拟合方法。如图5-2-20左上方的“指数拟合方法”控制按钮所示。

refine？：对拟合结果参数是否进一步精确，默认值为否。

amplitude：拟合模型的系数a。

damping：拟合模型的指数系数b，构成式5-2-12的指数拟合模型。

residue：余差，拟合模型的加权平均误差。

y=ae^bx （5-2-12）

图5-2-20 程序shixz05_07前面板

图5-2-21 指数拟合节点

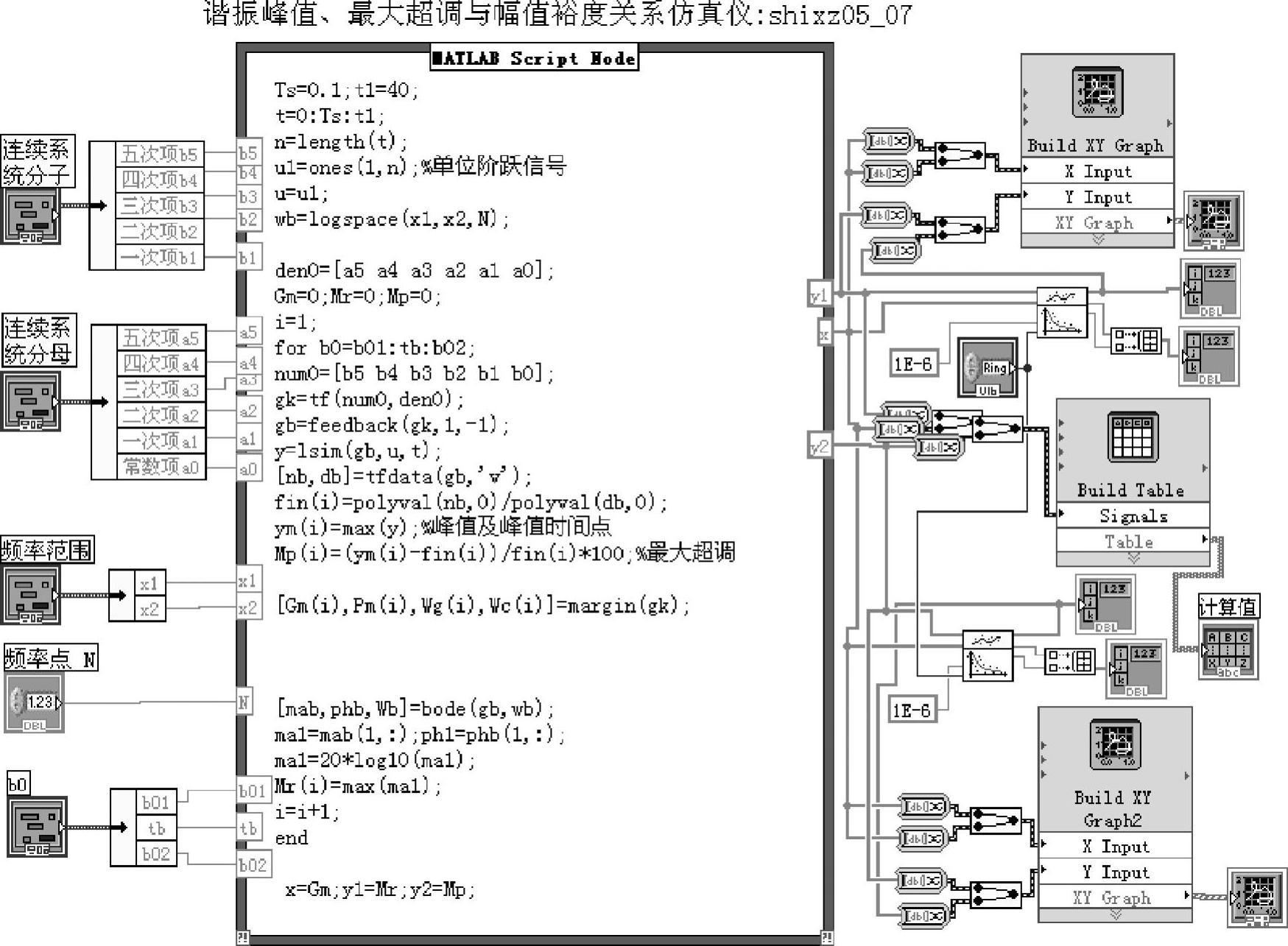
图5-2-22 程序shixz05_07框图面板

3.截止频率对快速性的影响

定性而言，系统闭环截止频率越高，快速性越好，上升时间、延迟时间和调整时间越短。但对于一般控制系统而言，截止频率对快速性影响的定量描述却是很困难的。它们之间关系的数字仿真分析见例5-8。

【例5-8】上升时间、调整时间与截止频率关系仿真分析仪。

系统闭环截止频率与其单位阶跃响应的上升时间、调整时间关系的数字仿真分析程序如shixz05_08所示。其程序框图面板和前面板分别如图5-2-23和图5-2-24所示。

程序说明：

程序shixz05_08与shixz05_07的结构相似。shixz05_08仿真曲线的自变量（横坐标）为闭环-3 dB截止频率ω_b，函数分别为闭环单位阶跃响应的上升时间和调整时间。拟合曲线数据采用LabVIEW的一般多项式拟合（General Polynomial Fit）节点获得。

程序采用for循环，在用户设定的步长和范围内改变系统的一个参数，获得一系列被研究的控制系统，计算每个系统的闭环截止频率。同时，在循环体内，针对每次循环所得系统，采用内插方式计算其上升时间和调整时间等快速性指标，然后将所得数据列成表格并绘制成仿真曲线。程序语句如图5-2-23所示，语句说明参见例5.3和例5.6。由于循环与内插后的数值都需要保存在相应的数组内，为了避免原保存值对新仿真数值的影响，必须将数组清零，否则仿真曲线会发生错误。特别是当参数变化范围缩小时，原有较大参数的数据将掩盖较小参数的仿真数据，仿真曲线可能被“冻结”而不发生变化。

图5-2-23 程序shixz05_08框图面板

由仿真曲线可见，系统的截止频率越大，也就是系统通频带越宽，系统的上升时间越小，具有单调下降的特点（参见图5-2-24）。不过，当截止频率达到一定值后，上升时间下降变缓，趋于饱和。调整时间与截止频率关系更为复杂。当等效阻尼比小于一定值之后，调整时间与带宽不再呈单调下降关系，而呈现类似锯齿波形的非单调关系，如图5-2-25所示。出现这种现象的原因之一是单位阶跃响应振荡曲线的振荡次数随着等效阻尼比和等效固有频率变化，进入误差带的波数也随之变化，进入而不越出误差带的时间点，即系统的调整时间可能因波数不同而发生前后交错，显示出与通频带的非单调下降关系。