控制系统瞬态时域性能指标及仿真分析

控制系统瞬态时域性能指标，通常以零初始条件下二阶振荡系统的单位阶跃响应为例进行讨论。其中部分指标已在第2章中作为二阶系统单位阶跃响应的特殊值介绍过，实际上瞬态性能指标并不受系统阶数的限制。设线性系统单位阶跃响应典型曲线如图5-1-12所示。

延迟时间t_d：响应从0首次达到稳态值的50%所用的时间。

上升时间t_r：响应从0首次达到稳态值的时间。也可定义成从10%稳态值到90%稳态值所经历的时间。

峰值时间t_p：响应第一次达到峰值的时间。

调整时间t_s：响应曲线进入偏离稳态值误差带Δ∈[2%，5%]的范围内并不再越出这一范围所需的时间，也称为过渡过程时间。

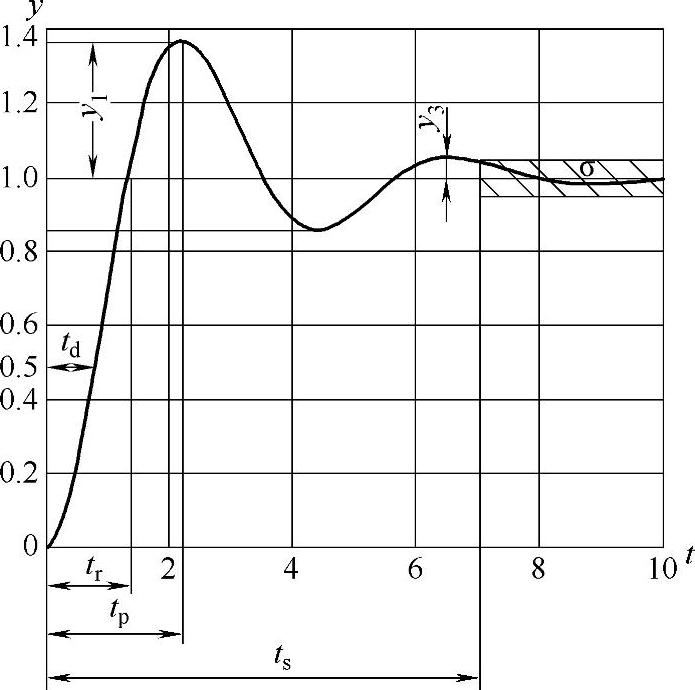
图5-1-12 线性系统单位阶跃响应典型曲线

振荡次数N：响应曲线在t_s之前围绕稳态值振荡的次数等于响应曲线穿越稳态值线次数的一半。例如图5-1-12的振荡次数为1.5次。

最大超调量M_p：响应峰值与稳态值之差与稳态值之比的百分数

在图5-1-12中，由于y（∞）=1，所以最大超调量可以表示为M_p=y₁%。最大超调量是一个相对概念，相应地，也可定义最大动态误差y₁，表示动态过程中偏离稳态的最大值。

衰减比n：振荡过程衰减快慢的指标，等于两个相邻同相波峰值之比。

衰减率φ：每经过一个振荡周期之后，振荡幅度衰减的百分数。

在上述各个动态指标中，最常用的是最大超调量M_p和调整时间t_s。前者反映了系统的最大动态误差，后者反映了系统的快速性。理论上希望二者都越小越好。综合考虑，工程上希望M_p不超过50%。由于被控对象不同，调整时间差别很大，很难有一个统一的标准。对于不同的控制系统，动态指标还有自己的特殊要求，例如对于生产线上的装配机械手和有些过程控制系统要求没有超调等。

如第2章所述，对于二阶系统，各项动态指标可以通过系统参数准确计算，但是对于一般控制系统，难于建立动态指标与系统参数之间的解析关系，通过数字仿真和实际测量是最适用的方法。

【例5-3】控制系统动态性能指标仿真测量仪。

控制系统动态性能指标仿真测量仪程序如shixz05_03所示，其程序框图面板和前面板分别如图5-1-13和图5-1-14所示。

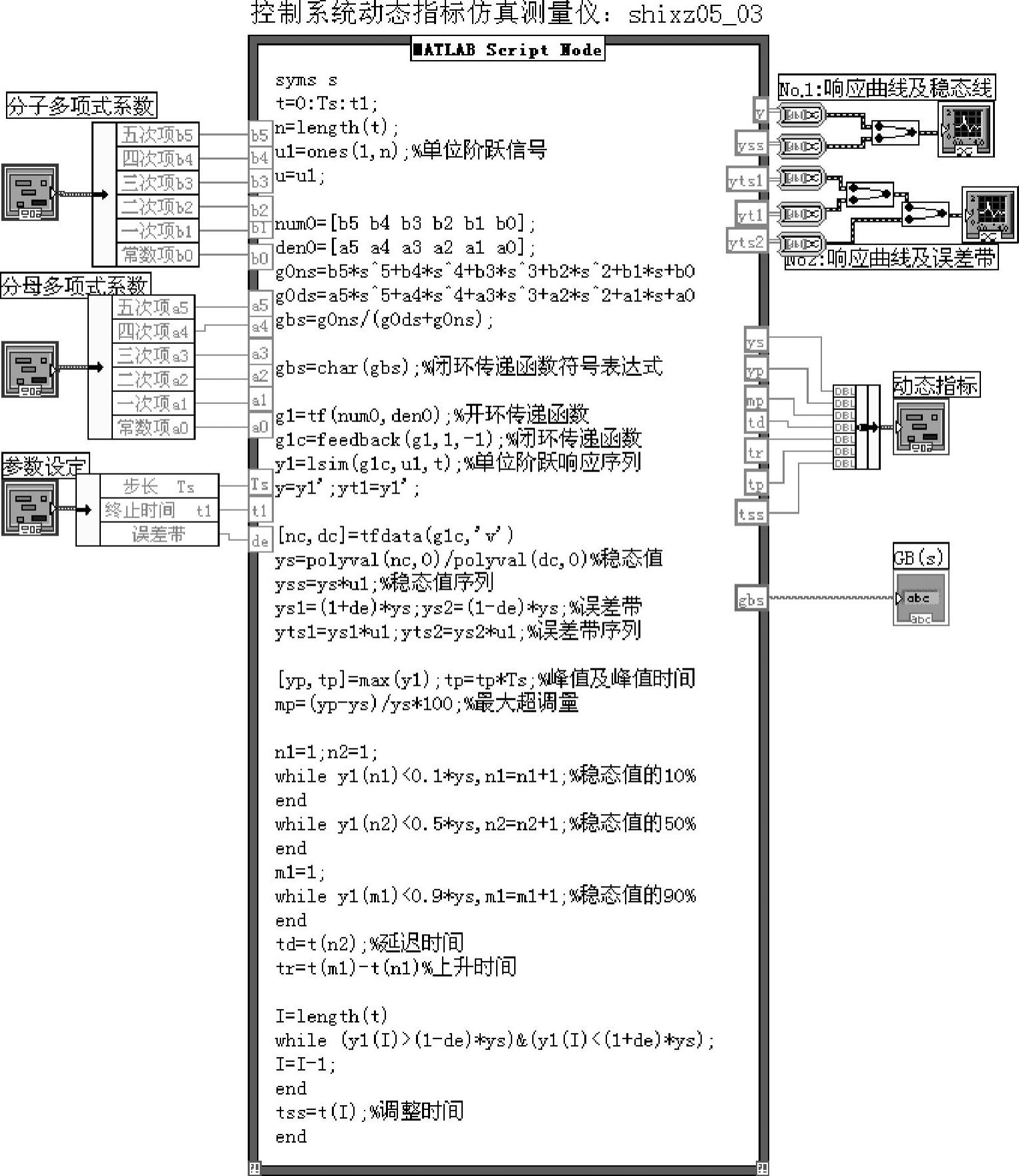
图5-1-13 程序shixz05_03框图面板

图5-1-14 程序shixz05_03前面板

程序说明：

参见前面板图5-1-14。该仿真测量仪通过系统的单位阶跃响应获取系统动态性能指标。(www.xing528.com)

用户对被控系统和仿真参数赋值，通过“开环系统设定”栏构成不高于五阶的开环传递函数。仿真参数赋值包括步长T_s，终止时间t₁和误差带de三项。通常误差带可以设定为0.02＜de＜0.05。

实例“开环系统设定”栏内使用Ⅰ型系统

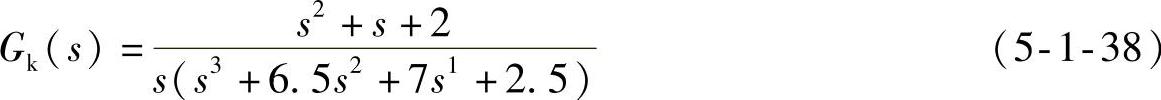
“动态指标”栏内显示下列各项瞬态性能指标。

1）响应稳态值y_s。该值通过单位阶跃响应的终值定理得到

仿真实例中G_k（s）见式5-1-38。显然，由于Ⅰ型系统是位置无差系统，其稳态值为1。实际程序语句为

当然，也可以通过求极限函数lim求得。

2）峰值y_p。通过下列语句求取响应序列的极大值：

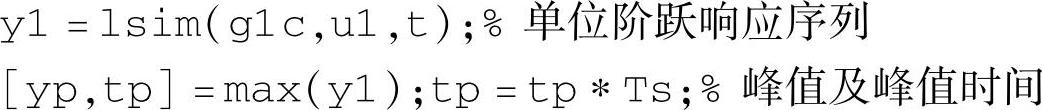
峰值和峰值时间的精度取决于计算步长T_s。

3）最大超调量M_p。按式（5-1-35）求取，程序语句为

4）延迟时间t_d，上升时间t_r，调整时间t_ss程序语句为

闭环传递函数的符号表达式示于前面板右下方。

前面板上设有两个示波器及其测量坐标系。No.1示出了响应曲线和稳态线，拖动沿响应曲线移动的测量游标，可以测量除调整时间以外的各项时间指标。例如，图5-1-13测得响应峰值时间为623×0.01s=6.23s，对应峰值为1.3938。该示波器还可以方便地测量并计算衰减比、衰减率等指标。

No.2示出了响应曲线和上下误差线，拖动沿响应曲线移动的游标也可以测量调整时间。同时可以看出振荡次数为2次。

注意：在绘制直线，例如稳态线和上下误差线时，必须获得与时间序列t点数相同的序列。稳态线使用如下语句：

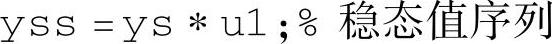
其中，u₁为单位阶跃序列，上下误差线语句类似。

在使用测量坐标系时，时间轴移动最小分格等于仿真步长T_s秒。鼠标单击测量坐标框上方菱形图案上的左右小菱形框，可以实现时间按步长的微小移动，便于准确对点。