控制系统稳态时域性能指标及仿真分析

控制系统的稳态时域性能指标包括静态误差、无静差度和开环比例系数等。其中最基本的是静态误差e_ss。静态误差又称稳态误差。显然，静态性能指标是在系统稳定的前提下进行讨论的。

在反馈控制系统中，误差由输入及系统结构共同决定，其基本表达式为

式中，G_k（s）为系统的开环传递函数，X_i（s）为系统输入的象函数。由终值定理，稳态误差为

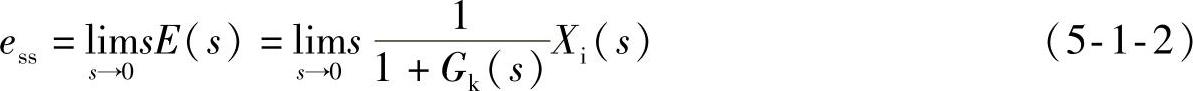
1.由系统输入所产生的稳态误差

1）单位阶跃输入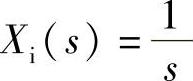：，所以

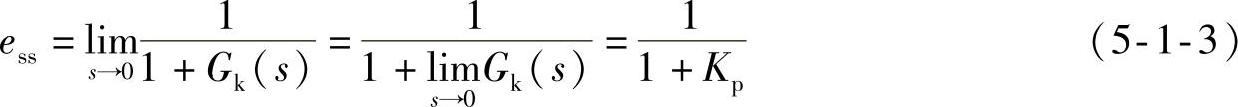
式中，

称为系统的稳态位置误差系数，仅由系统开环传递函数决定。

2）单位恒速输入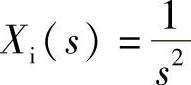：，所以

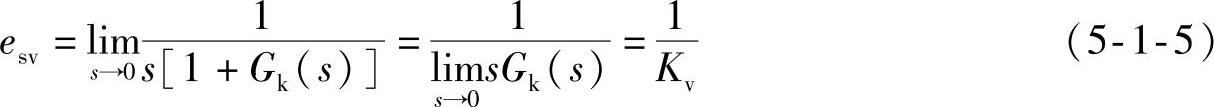
式中，

称为系统的稳态速度误差系数，由系统开环传递函数与s的积决定。

3）单位恒加速输入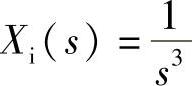：，所以

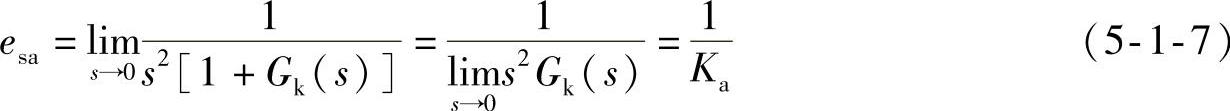
式中，

称为系统的稳态加速度误差系数，由系统开环传递函数与s²的积决定。

2.开环系统结构（型次）与稳态误差的关系

由式（5-1-4）、式（5-1-6）和式（5-1-8）可知，稳态位置、稳态速度和稳态加速度误差系数具有依次微分的关系。它们的最终结果取决于系统结构，即开环传递函数的形式，这里称系统开环传递函数中包含积分环节（1/s）的个数为系统的型次。也就是说，在输入确定的情况下，系统的稳态误差系数，进而系统的稳态误差，完全取决于系统的型次。

1）0型系统的稳态误差系数及稳态误差（G_k（s）分母中不含因子s）：

2）Ⅰ型系统的稳态误差系数及稳态误差（G_k（s）分母中含有因子s）：

3）Ⅱ型系统的稳态误差系数及稳态误差（G_k（s）分母中含有因子s²）：(www.xing528.com)

由上分析可知，0型系统总是有差系统，而且仅能适应阶跃输入（稳态位置误差为有限值）；Ⅰ型系统是位置无差系统，速度有差系统，不适应加速输入；Ⅱ型系统是加速度有差系统，位置和速度无差系统。这表明，在系统稳定的前提下，开环传递函数所含的积分环节，有利于减少稳态误差。仿真实例见例5-1。

【例5-1】控制系统输入稳态误差仿真仪。

一个闭环稳定系统由输入产生的稳态误差仿真仪程序如shixz05_01所示，其框程序图面板和前面板分别如图5-1-2和图5-1-3所示。

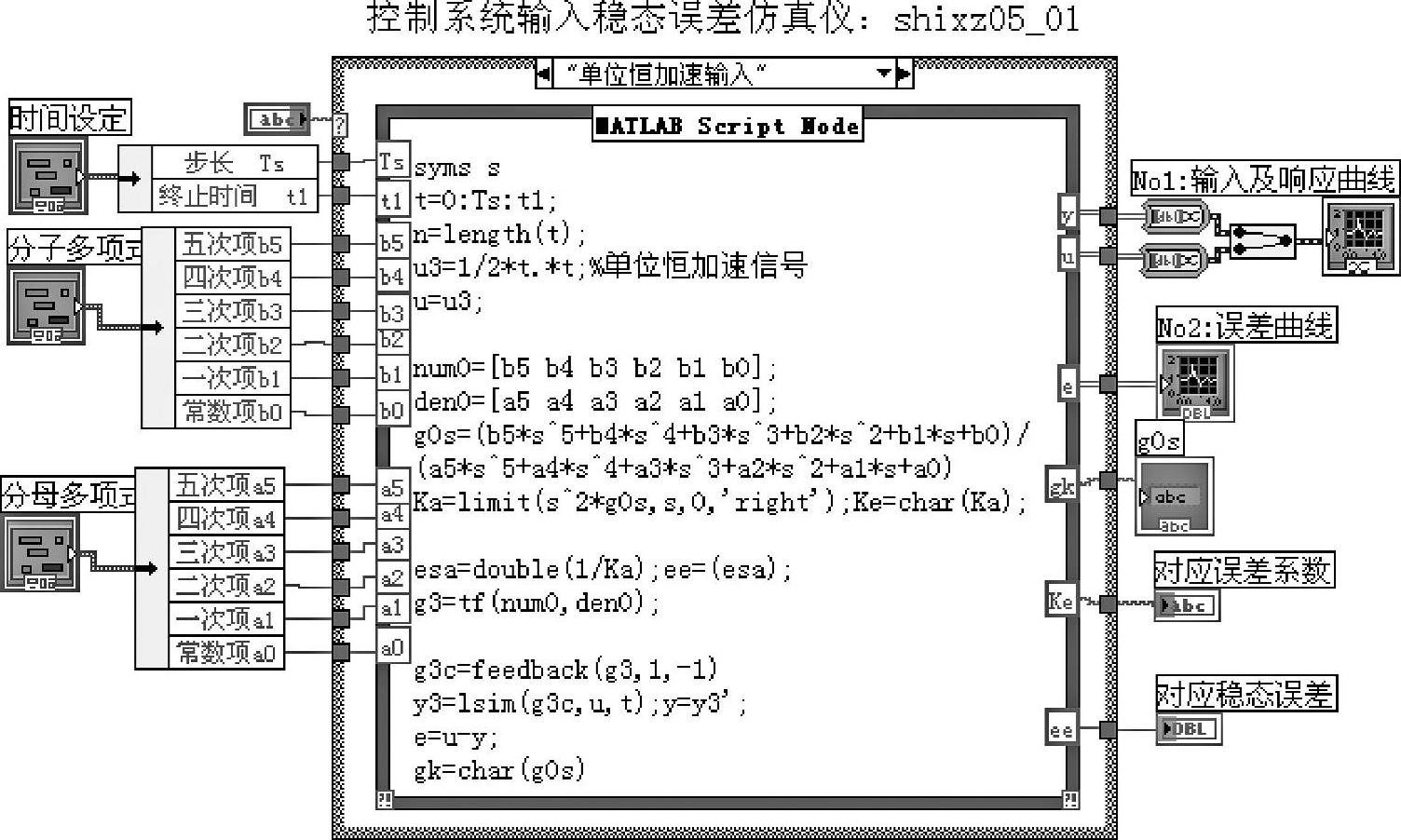
图5-1-2 程序shixz05_01框图面板

程序说明：

由前面的分析可知，系统由输入产生的稳态误差取决于输入信号和开环系统的型次。该仿真仪可以对开环系统的型次与输入的不同组合所产生的稳态误差进行仿真。

1）系统型次的设定。程序前面板“开环系统设定”栏最大可以设定如下的五阶系统

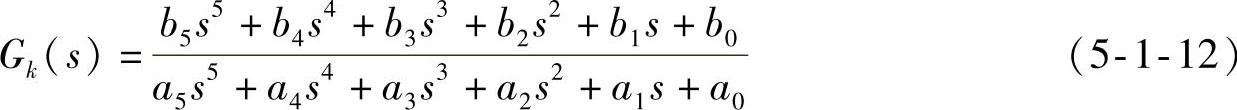
通过适当设定分子、分母系数的值，可以设定不高于五阶的各型开环系统。当a₀≠0时为0型系统，当a₀=0而a₁≠0时为Ⅰ型系统，当a₀、a₁均为零而a₂≠0时为Ⅱ型系统。实际仿真使用的开环传递函数a₀=0，示于前面板的最下方“g0s开环传递函数G_k（s）”栏内，为一个四阶Ⅰ型系统：

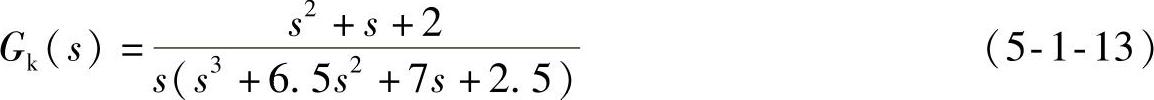
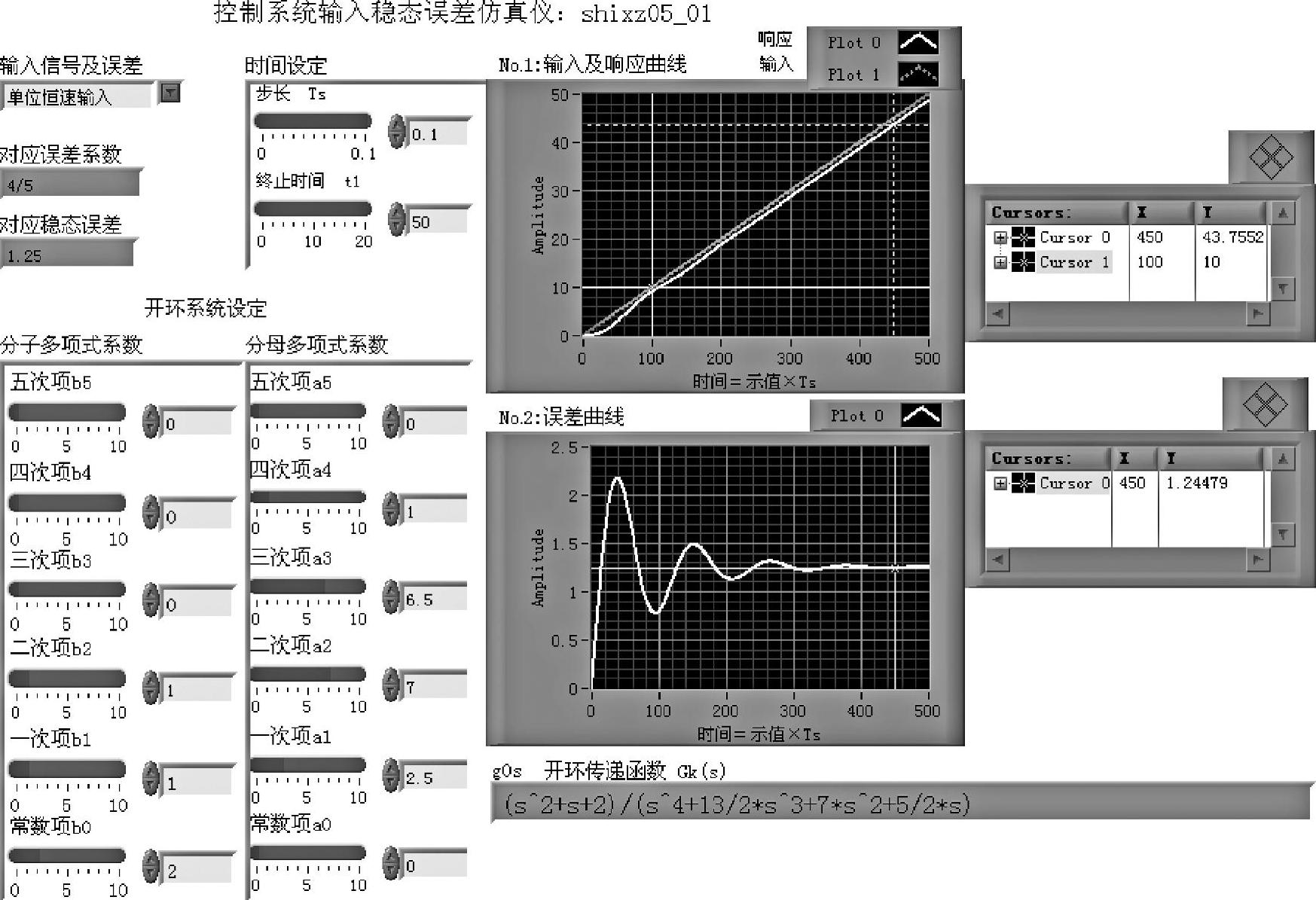
图5-1-3 程序shixz05_01前面板

2）输入及误差选择。“输入信号及误差”单选框设置了单位阶跃、单位恒速和单位恒加速输入3条可选项，如图5-1-4所示。

该单选框同时完成与输入一致的误差系数及误差的选择，如图5-1-3所示。当选择单位恒速响应时，其对应的稳态速度误差系数及稳态速度误差的计算值示于开关下面的两个框内，如图5-1-5b所示。图5-1-5a、c分别示出实例的单位阶跃和单位恒加速输入时的稳态误差信息。

图5-1-4 输入及误差单选框

图5-1-5正是式（5-1-10）所述的I型系统稳态误差系数及稳态误差的仿真结果。

图5-1-5 不同输入的误差系数及稳态误差

3）响应及误差曲线。程序前面板设有两个示波器面板，为No.1显示输入曲线及对应的闭环响应曲线，No.2显示误差曲线。所仿真的Ⅰ型系统的误差曲线如图5-1-6所示，其中分别表示位置误差、速度误差和加速度误差曲线。该图清楚可见Ⅰ型系统稳态位置无差、速度有差、加速度误差无穷大的趋势。

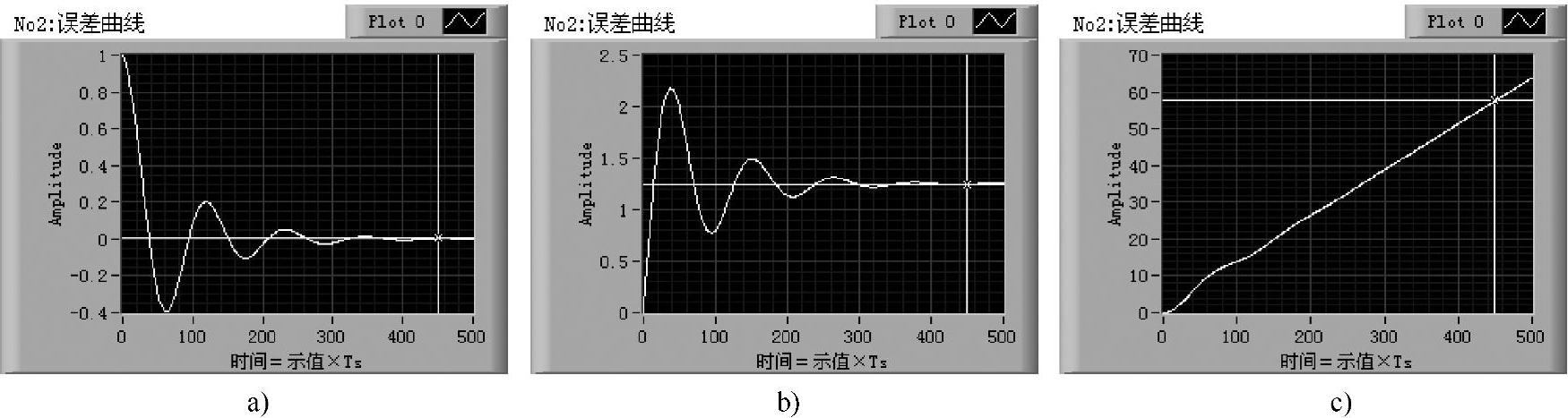
图5-1-6 误差曲线

在计算误差系数时，需要求极限，可以在MATLAB的符号工具箱内调用limit函数，其调用格式为

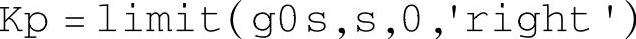
该语句可以完成式（5-1-4）的数学运算。语句中的g0s是系统开环传递函数的表达式，′right′表示求取右极限。