1.李雅普诺夫方程
使用李雅普诺夫方程的线性定常系统仿真见例4-6和例4-7。
【例4-6】连续线性定常系统李雅普诺夫方程仿真分析仪。
连续线性定常系统李雅普诺夫方程稳定性判别仿真分析仪程序如shixz04_06a所示,程序框图面板和前面板分别如图4-6-1和图4-6-2所示。
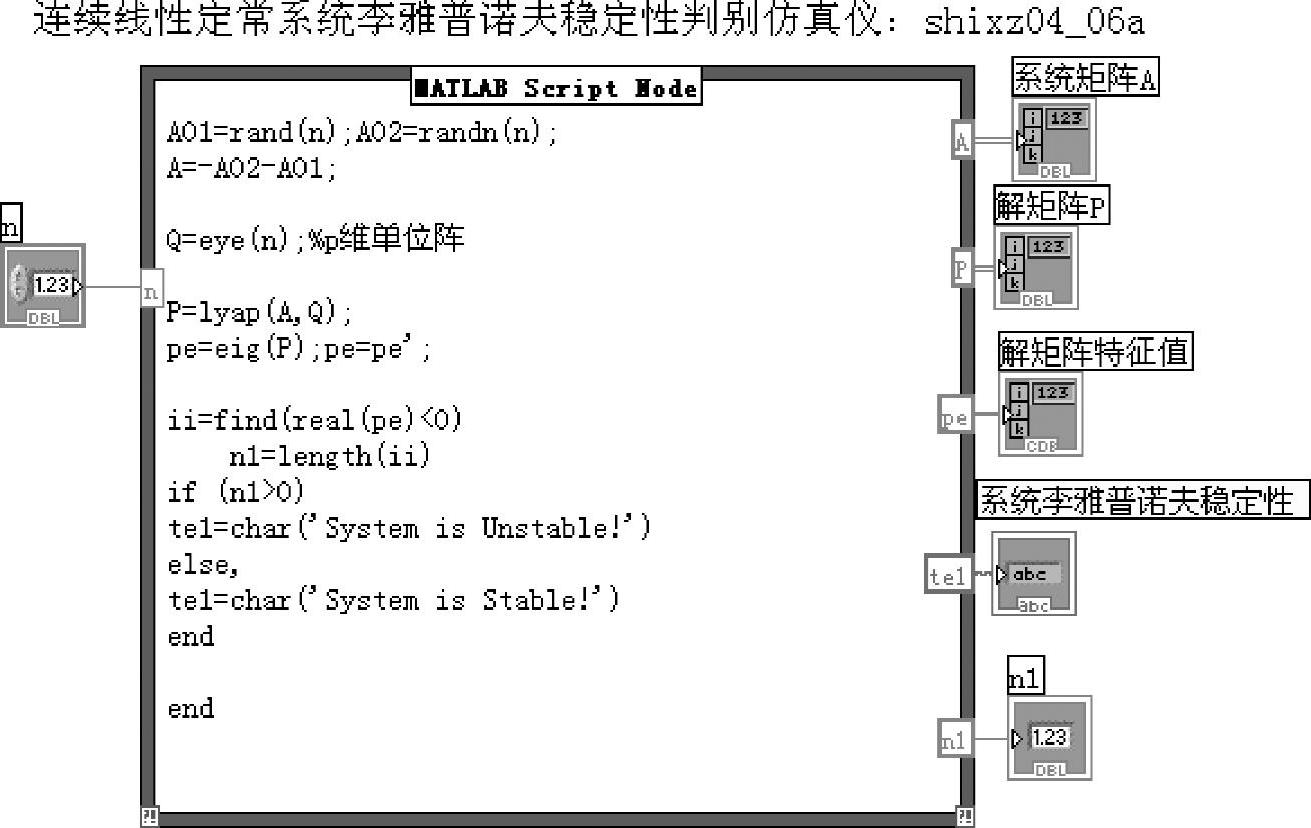
图4-6-1 程序shixz04_06a框图面板
程序说明:
程序求解连续线性定常系统的李雅普诺夫方程式(4-6-7)。基本命令格式为
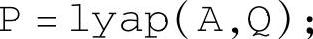
语句中矩阵A为随机生成的n阶齐次方程

的系统矩阵,Q为n维单位阵。
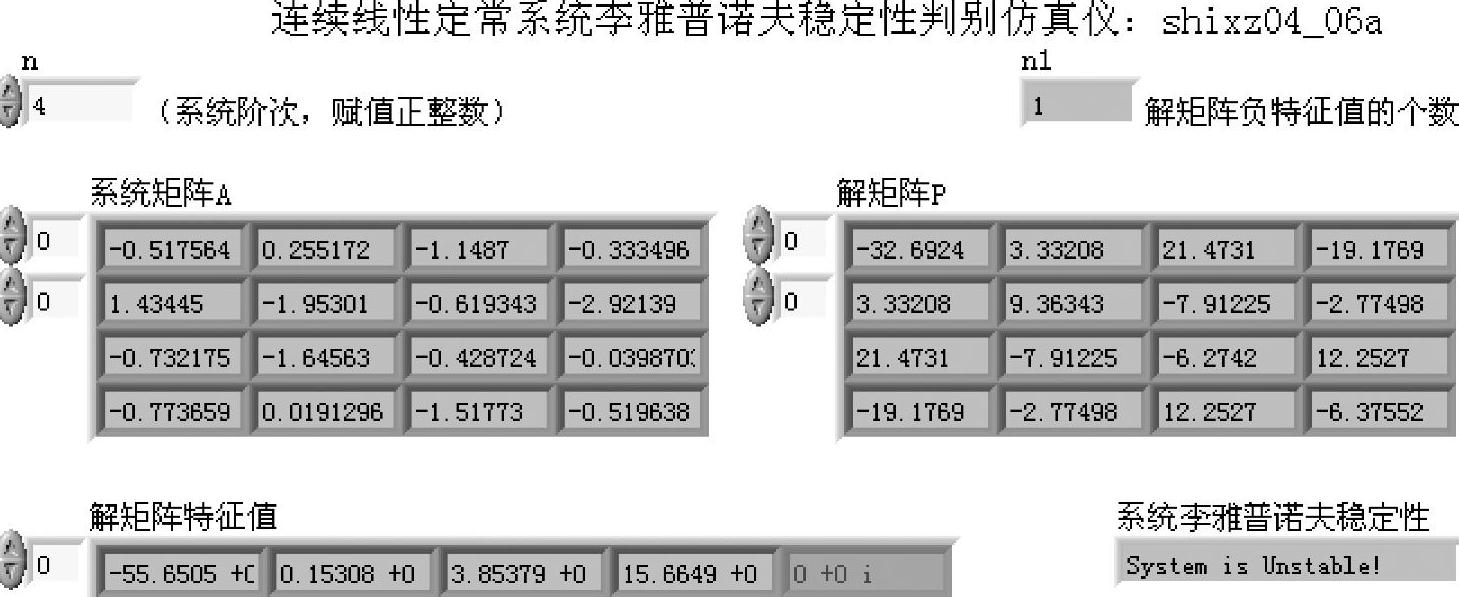
图4-6-2 程序shixz04_06a前面板
用户在前面板输入需要求解的方程阶次n,系统随机生成系统矩阵A,并求出李雅普诺夫方程式(4-6-7)的解矩阵P。由于矩阵A为实数阵,所以P为实对称阵。实对称阵正定的充要条件是其全部特征值大于零。程序在使用函数pe=eig(P)求出P的特征值后,使用下列语句判断其是否全部大于零,并显示系统的稳定性:

语句find(real(pe)<0)找出P中负特征值,并将其位置和个数存于数组ii中。语句n1=length(ii)将负特征值个数存于变量n1中,再由if语句判断n1是否大于零(P是否存在负特征值)来判断P是否正定,从而判断连续线性定常系统是否稳定。
程序前面板给出了P的特征值及负特征值的个数n1,最后给出系统稳定性判定结论。
程序shixz04_06b为在前面板上手动设置系统矩阵的仿真实例。
【例4-7】离散线性定常系统李雅普诺夫方程分析仿真仪。
离散线性定常系统李雅普诺夫方程稳定性判别仿真仪程序如shixz04_07a所示,程序框图面板和前面板分别如图4-6-3和4-6-4所示。
程序说明:
程序shixz04_07a与程序shixz04_06a类似。不同之处在于,本例通过离散随机状态空间模型函数drss生成离散状态空间系统,再由函数dssdata取出系统矩阵F。由于函数drss总是生成稳定随机离散系统,为了加大系统稳定性的随机性,程序采用两个稳定随机系统矩阵相加的方式构成实际仿真的系统矩阵。
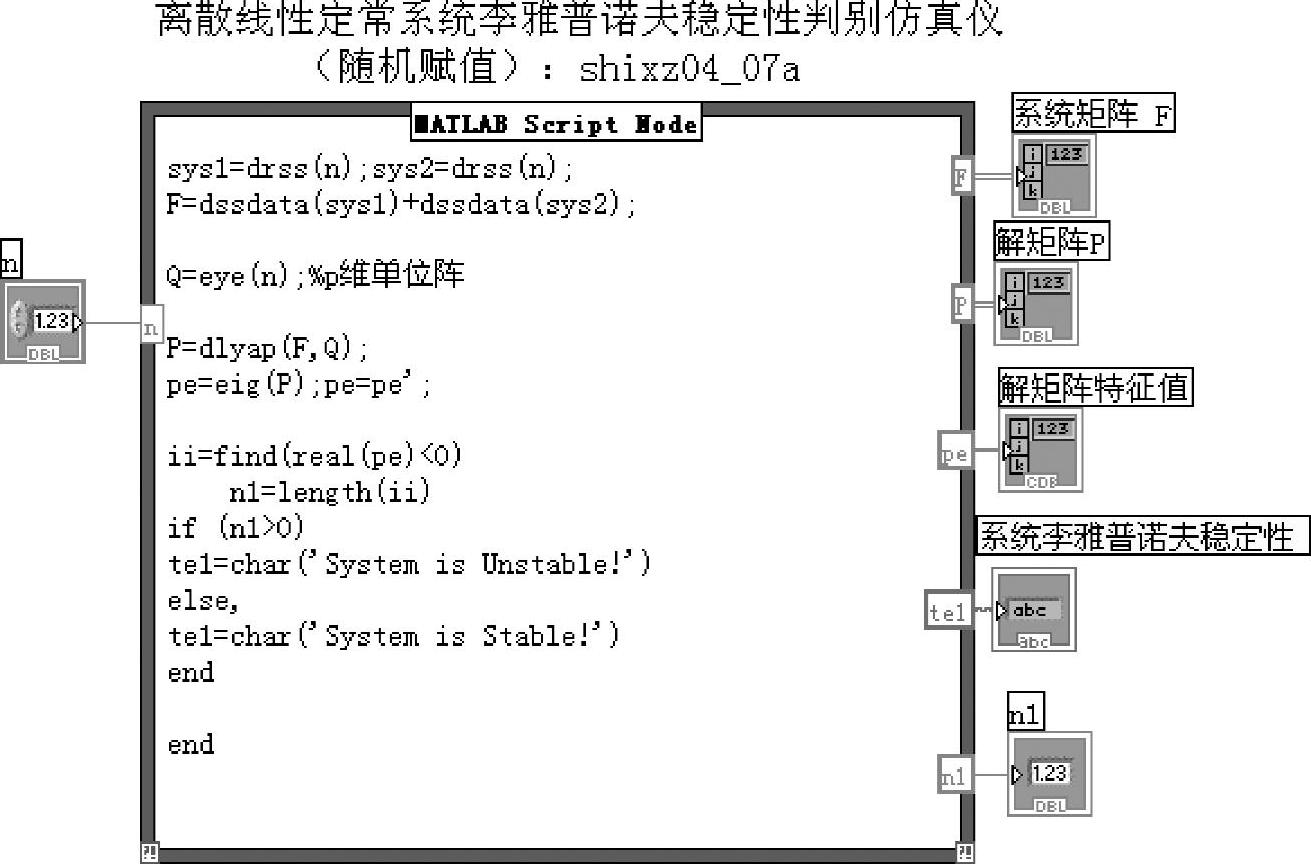
图4-6-3 程序shixz04_07a框图面板
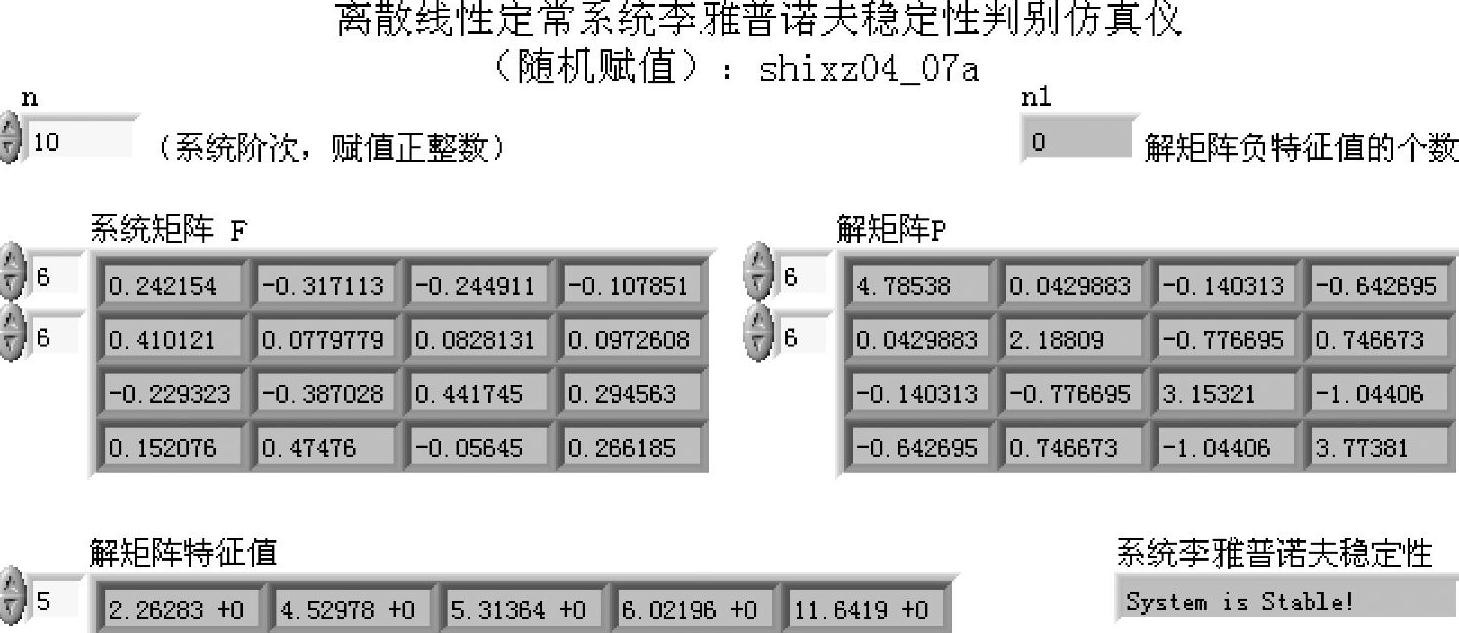
图4-6-4 程序shixz04_07a前面板
仿真实例给出了一个10阶随机离散系统。前面板通过数组索引显示出系统矩阵和对应解矩阵的最后4行4列。解矩阵的特征值数组给出了后面5个特征值,注意离散李雅普诺夫方程式(4-6-9)判别稳定性的结论仍然是解矩阵P正定。图4-6-4示出某次运行后P的所有特征值都大于零。读者可以验证,此时系统矩阵F全部特征值的模都小于1。
程序shixz04_07b为手动设置系统矩阵的仿真实例。
2.李雅普诺夫第一方法仿真实例
使用线性化方法研究一些弱非线性系统在平衡点附近的稳定性,得出式(4-6-3)。仿真实例见例4-8。
【例4-8】李雅普诺夫第一方法稳定性判别仿真分析仪。
一些弱非线性系统在平衡点附近稳定性的李雅普诺夫判别法参见4.6.1节。仿真仪程序如shixz04_08所示,程序框图面板和前面板分别如图4-6-5和图4-6-6所示。
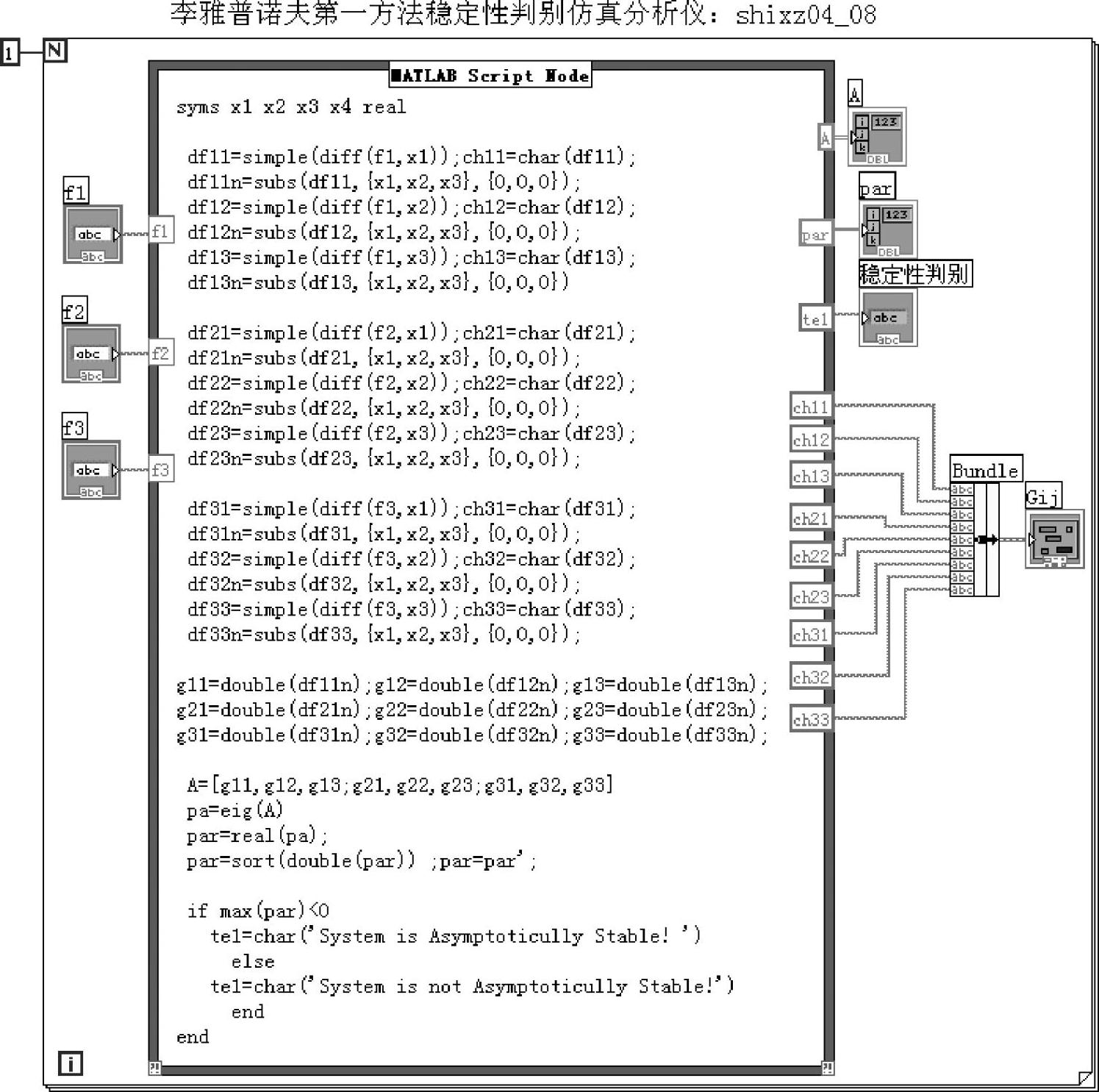
图4-6-5 程序shixz04_08框图面板
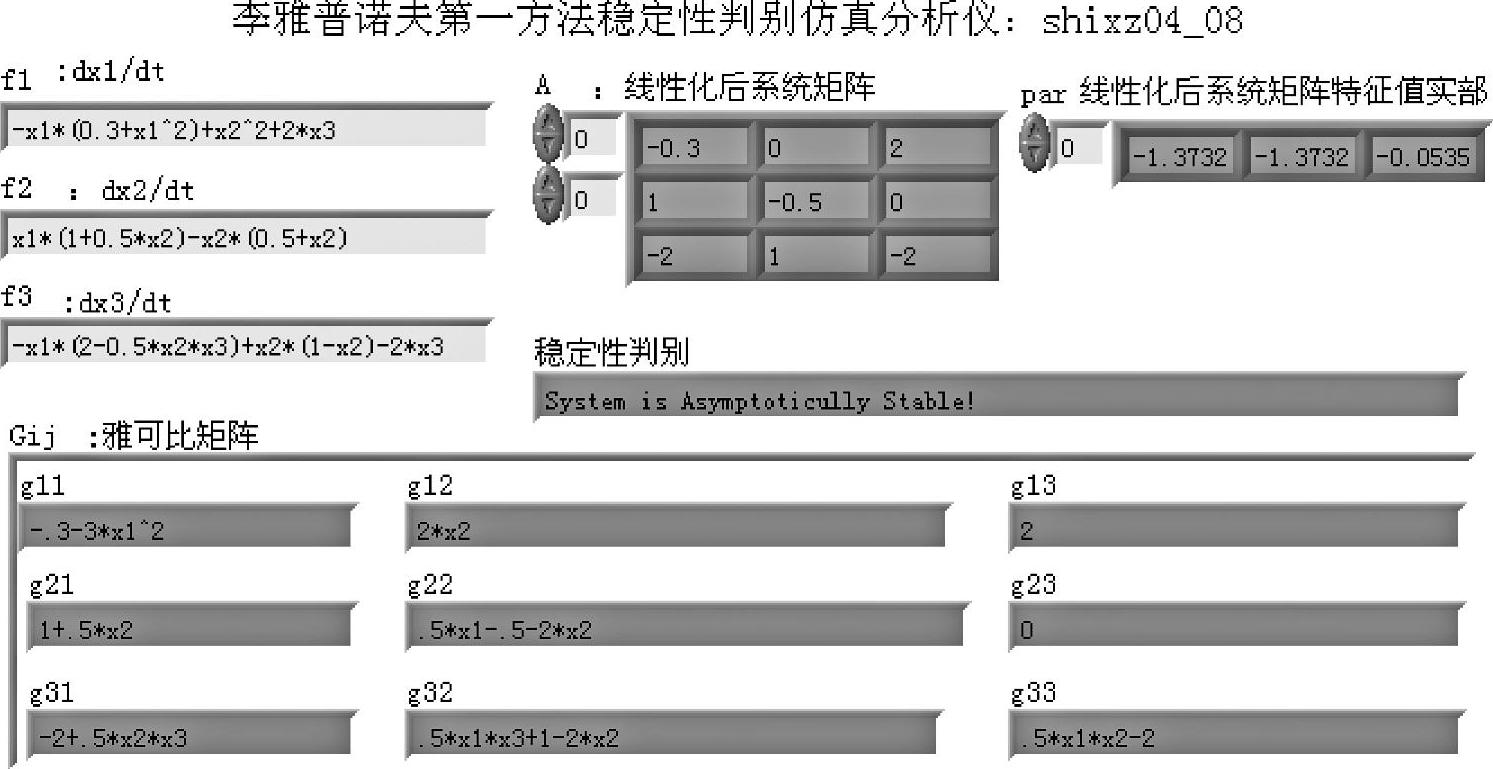
图4-6-6 程序shixz04_08前面板
程序说明:
程序shixz04_08a在MATLAB符号工具箱环境下工作。用户在前面板上键入3阶非线性系统
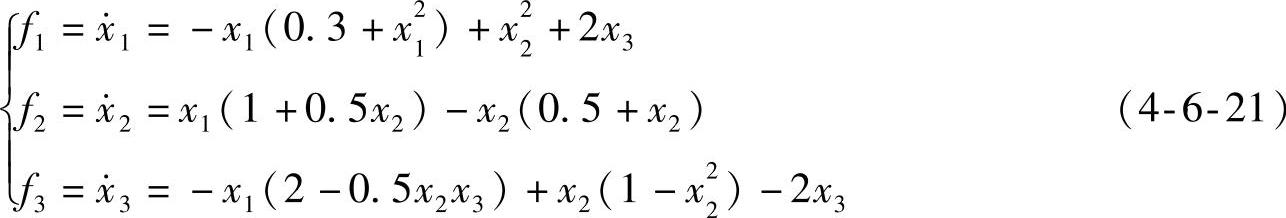
程序使用求导函数
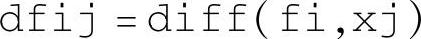
求出式(4-6-3)的雅可比矩阵元表达式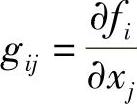 (i,j=1,2,3),显示于前面板字符串簇Gij之中。然后使用替换函数
(i,j=1,2,3),显示于前面板字符串簇Gij之中。然后使用替换函数
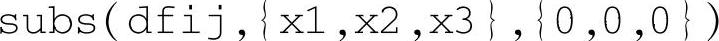
求出雅可比矩阵在平衡点附近的数值矩阵A,最后通过判断矩阵A有无正实部特征值来判断原非线性系统的渐近稳定性。矩阵A的特征值实部及渐近稳定性结论都示于前面板上。对于零特征值情况,仿真程序显示非渐近稳定,但是否稳定需另作判断,该程序不给出结论。
线性化方法得出的稳定性结论适应于平衡点附近的局部范围,非线性系统本身的稳定性与初始状态有关。相应的仿真分析见例4-9。
【例4-9】非线性系统的数值解仿真分析仪[9]。
程序shixz04_09给出了系统式(4-6-21)的状态数值解仿真曲线。程序框图面板和前面板分别如图4-6-7和图4-6-8所示。
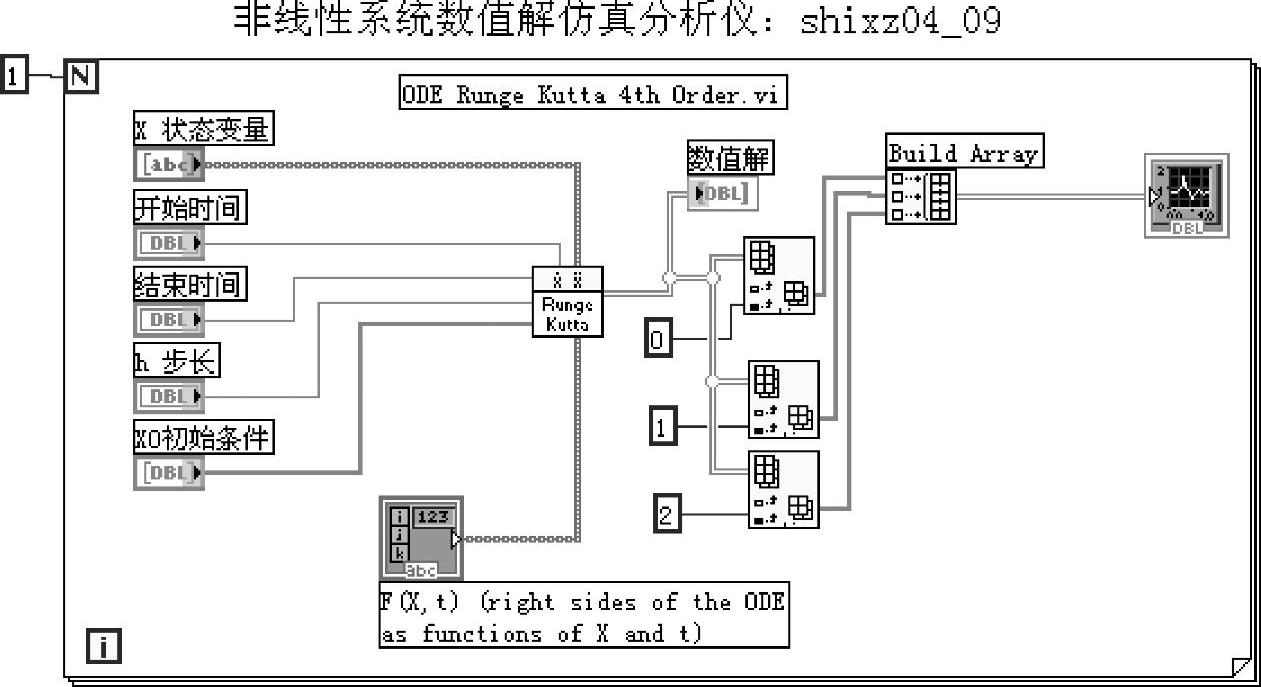
图4-6-7 程序shixz04_09框图面板
程序说明:
程序使用LabVIEW提供的四阶龙格库塔算法节点直接求出非线性系统的数值解,再使用示波器节点给出仿真曲线。四阶龙格库塔算法节点的路径为Mathematics\DifferenticalEquation\ODE Runge Kutta 4 th Order.vi,图标如图4-6-9所示。
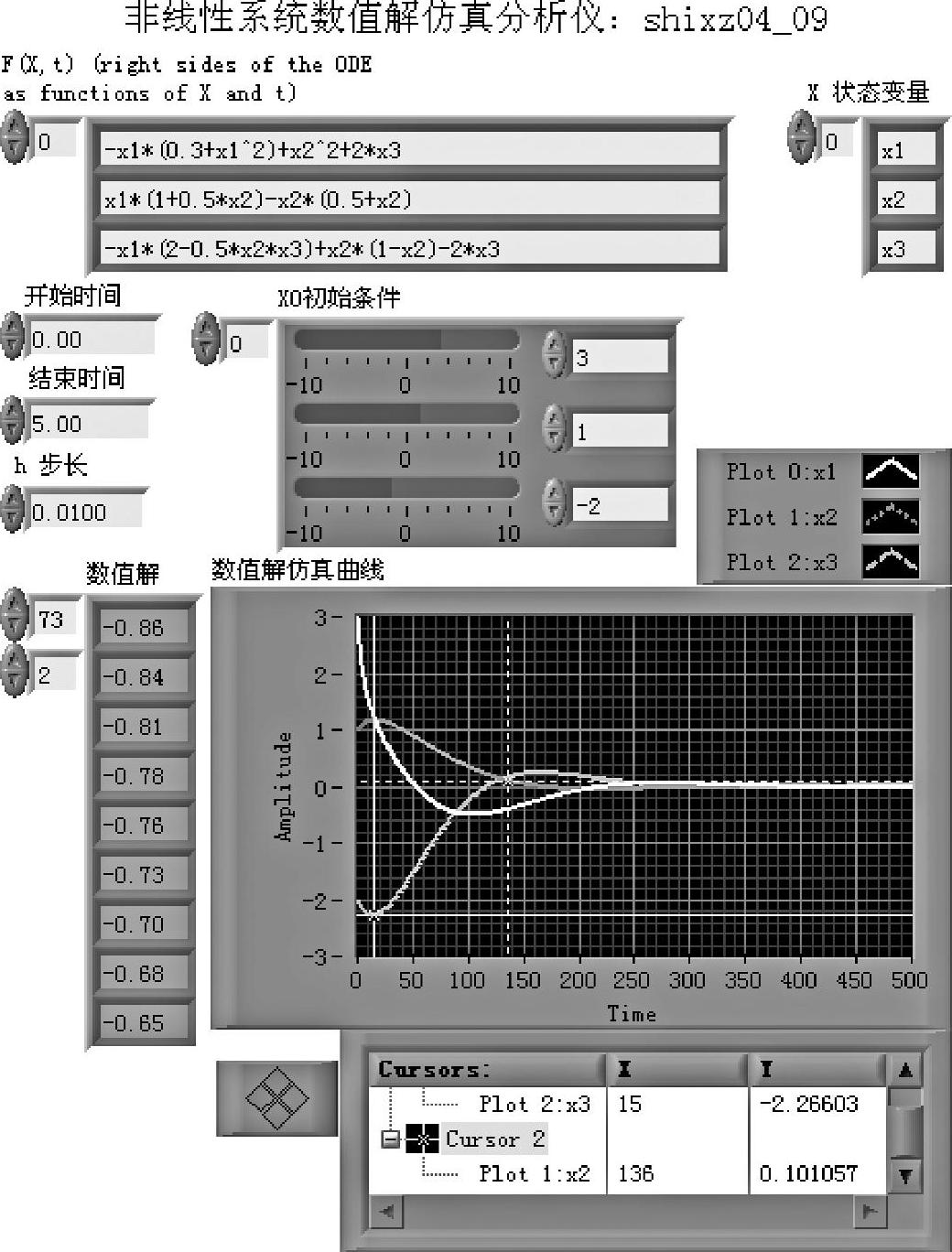
图4-6-8 程序shixz04_09前面板
图4-6-9中的变量名称端口X和函数F(x,t)都是1维字符串数组,要求用户赋值时使用相同变量名,例如x1、x2、x3或x、y、z等,如图4-6-8的上部所示。起止时间、步长和初始状态设定如图4-6-8的中部所示;数值解及其仿真曲线如图4-6-8的下部所示。
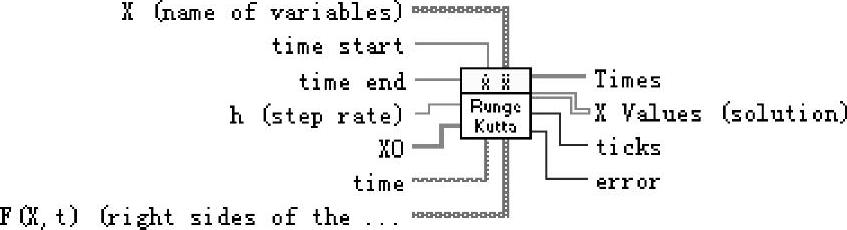
图4-6-9 4阶龙格库塔算法节点
参见图4-6-8,非线性系统式(4-6-21)在所设定的初始状态下是渐近稳定的,这与例4-8的结论相同。但是由于非线性系统的稳定性与初始状态密切相关,在其他条件不变的情况下,连续拖动程序shixz04_09前面板的初态滑竿改变初态X0的值,可见仿真曲线连续变化,由收敛变至发散。如图4-6-10所示,在所给的初态下,系统发散趋势已明显可见。
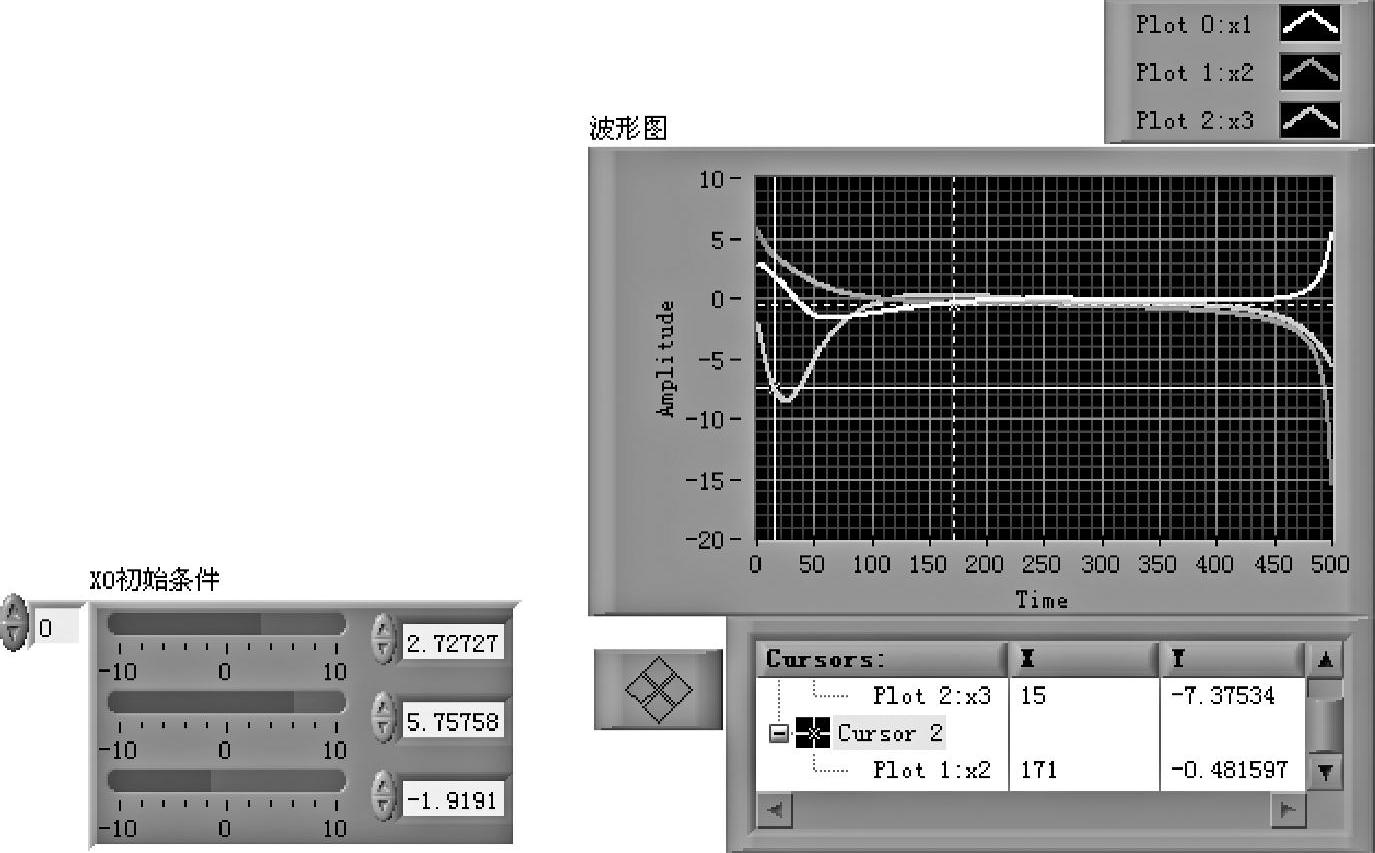
图4-6-10 初态对非线性系统稳定性的影响
3.克拉索夫斯基方法仿真实例(https://www.xing528.com)
【例4-10】克拉索夫斯基方法仿真分析仪。使用克拉索夫斯基方法分析系统式(4-6-22)中a,b对稳定性的影响,绘制系统解的仿真曲线。

运行如下程序:

得到系统负雅可比矩阵
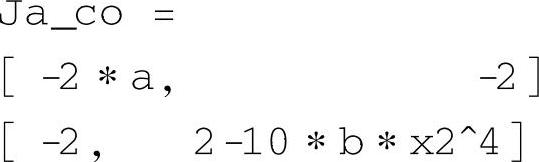
按照塞尔维斯特定理,负雅可比矩阵正定要求
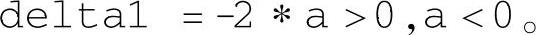
和
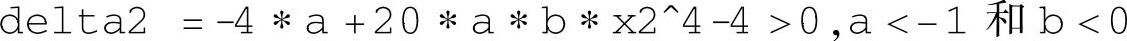
负雅可比矩阵正定的充分条件为a<-1和b<0。
仿真曲线程序如shixz04_10所示,前面板及程序框图面板分别如图4-6-11和图4-6-12所示。

图4-6-11 程序shixz04_10前面板
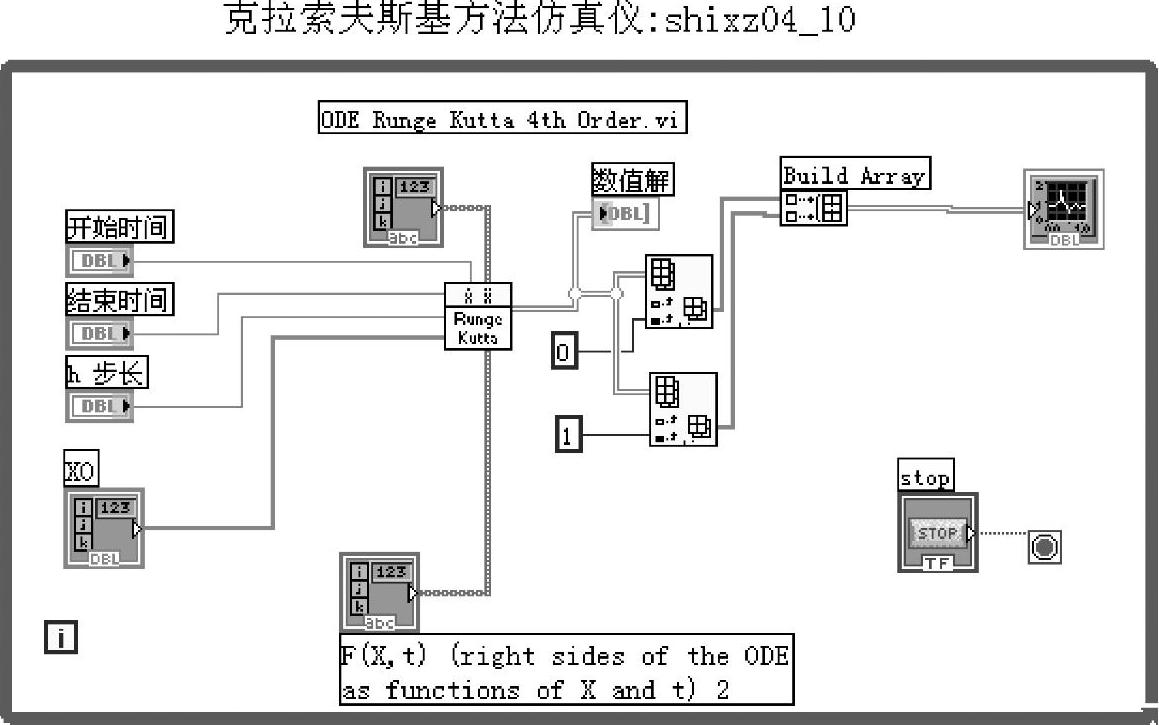
图4-6-12 程序shixz04_10框图面板
仿真曲线按充分条件时取a=-1.5,b=-1。此时,
当x→∞,V(x)=(-1.5x1+x2)2+(x1-x2-x52)2→∞
所以平衡态Xe=0是大范围渐近稳定的。
当取a=-1,b=0.01时,雅可比矩阵非负定,克拉索夫斯基方法不提供有关稳定性的信息。但仿真表明,虽然不满足克拉索夫斯基的充分条件,但系统在小范围仍然是渐近稳定的。仿真曲线如图4-6-13所示。

图4-6-13 不满足克拉索夫斯基充分条件的仿真曲线图
【例4-11】变量梯度法仿真仪。
使用变量梯度法研究系统式(4-6-23)的稳定性,列出各个主要步骤的结果。

本例采用计算机与人工相互配合的方式说明使用变量梯度法寻找李雅普诺夫函数的主要步骤,程序如shixz04_11所示,程序框图面板和前面板分别如图4-6-14和图4-6-15所示。
输入赋值:打开程序shixz04_11,前面板如图4-6-15所示。在“f1:dx1/dt”输入框内输入-x1+2*x1^2*x2,在“f2:dx2/dt”输入框内输入-x2。对于二阶系统式(4-6-23),按照式(4-6-15)设定其李雅普诺夫函数梯度的两个分量分别为a11*x1+a12*x2,a21*x1+a22*x2,并将其填入“del1:李函数梯度1”和“del2:李函数梯度2”框内。对应框图面板内的程序语句为
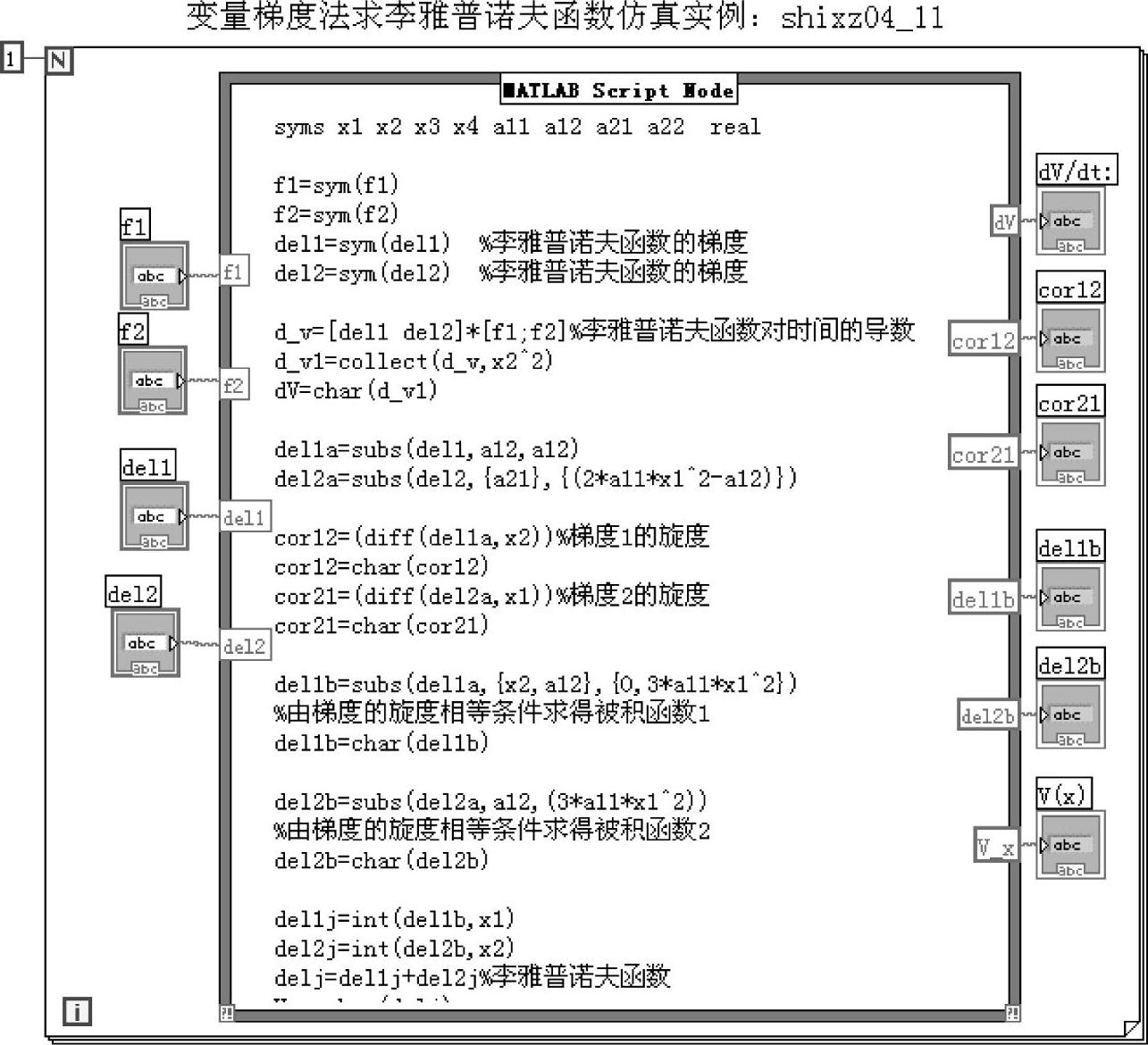
图4-6-14 程序shixz04_11框图面板

图4-6-15 程序shixz04_11前面板图

运行该程序后的前面板如图4-6-15所示。程序求出李雅普诺夫函数对时间的导数
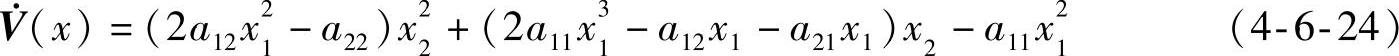
示于“dV/dt:李函数对时间的导数”框内。对应程序语句为

系统稳定性要求李雅普诺夫函数对时间的导数dV/dt<0。对于本例,可以令式(4-6-24)中a11>0,a22>2a12x21和
2a11x21-a12-a21=0,即a21=2a11x21-a12 (4-6-25)
将式(4-6-25)代回李雅普诺夫函数梯度的第二个分量,消去a21得
(
2a11x21-a12)x1+a22x2
对应程序语句为
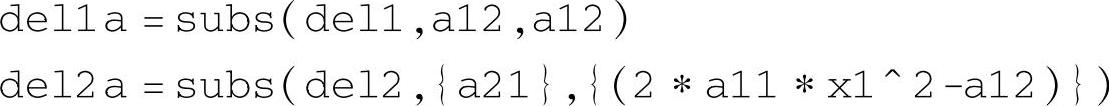
再按照式(4-6-19)求该梯度的旋度,结果示于“cor12:旋度1”和“cor21:旋度2”两个框内,令其相等得到
a12=3a11x21 (4-6-26)
对应程序语句为

将式(4-6-26)再代回梯度表达式,获得按式(4-6-18)所选路径的两个积分的被积函数,结果示于“del1b:被积函数1”和“del2b:被积函数2”两个框内,对应程序语句为
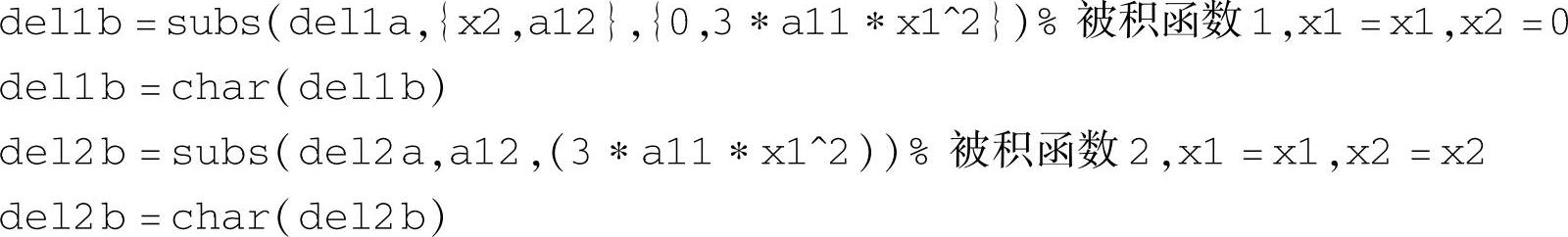
最后,按式(4-6-18)规定的积分限积分,求出本例的李雅普诺夫函数,示于“V(x):李雅普诺夫函数”框内,对应的程序语句为

考察本例所获得的李雅普诺夫函数正定的条件,即要求积分结果
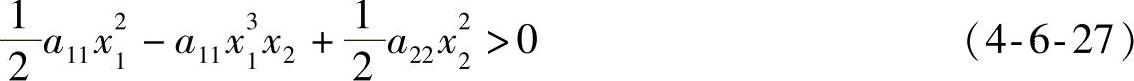
即要求二次型
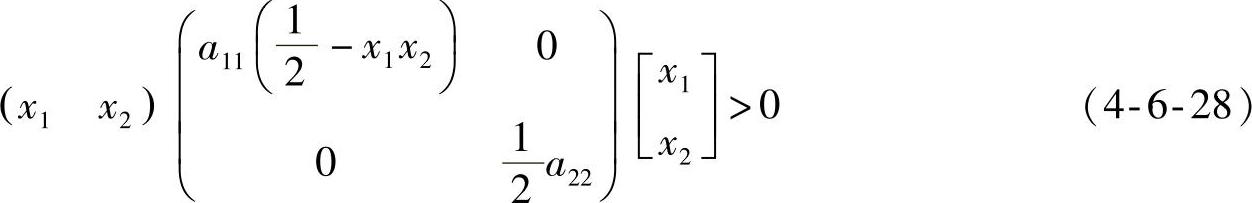
当a11、a22>0,在x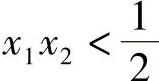 的范围内,可以保证V(x)>0和
的范围内,可以保证V(x)>0和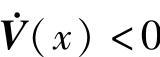 。
。
借用程序shixz04_08c的“4阶非线性系统数值解仿真仪”,可以获得系统式(4-6-23)解的仿真曲线,如图4-6-16所示。由于变量梯度法获得的也是稳定性的充分条件,所以初始条件可以比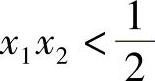 更宽一些。读者可以使用连续运行方式,拖动初始条件滑杆进行实验。
更宽一些。读者可以使用连续运行方式,拖动初始条件滑杆进行实验。
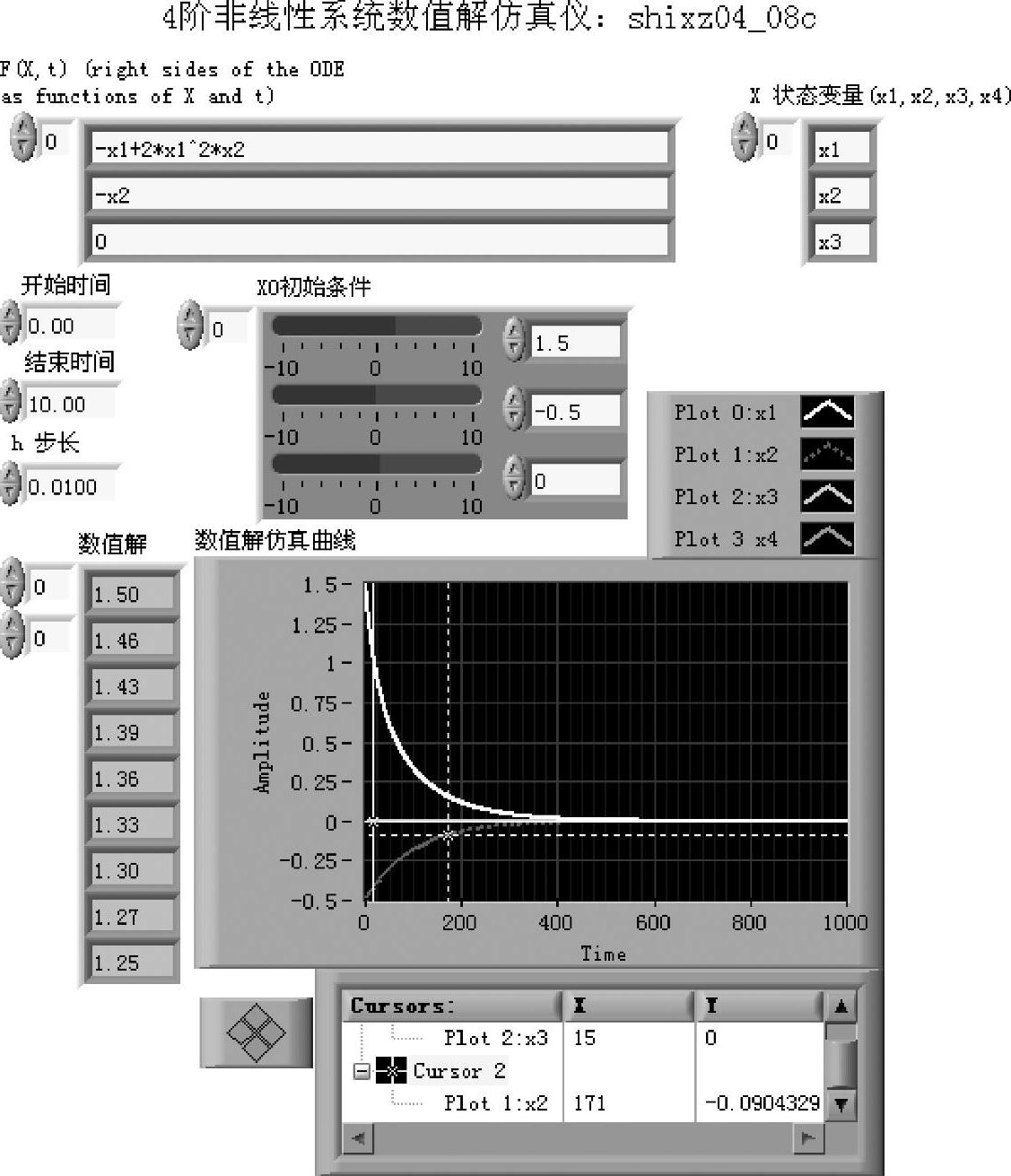
图4-6-16 程序shixz04_08c前面板
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




