运用李雅普普诺夫第二方法分析非线性系统稳定性

前已述及，运用李雅普诺夫第二方法分析非线性系统稳定性的难点在于寻找合适的李雅普诺夫函数V（X），而构造V（X）尚无一个普遍的方法，下面介绍几种常用的方法。

1.克拉索夫斯基方法

对原点为平衡态的非线性系统

取李雅普诺夫函数为右端向量函数的二次型V（X）=f^T（X）f（X） （4-6-13）

对式（4-6-13）求时间的导数有

式中，J（X）为雅可比矩阵。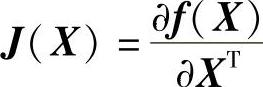

判别方法为，若式（4-6-14）中的J^T（X）+J（X）＜0，则系统式（4-6-12）一致渐近稳定。

克拉索夫斯基方法得出的也是充分条件。使用克拉索夫斯基方法要求向量函数f（X）中的第i个分量f_i（X）中必须含有x_i为自变量，以保证雅可比矩阵对角线元素不为零。

2.变量梯度方法^[8]

假定已经求出的李雅普诺夫函数V（X）具有单值梯度▽V并且可以表示成如下形式：

式中，待定系数a_ij（i，j=1，2，…，n）通常假定为常数或t的函数。

导数和梯度▽V之间有如下关系(www.xing528.com)

函数V（X）是其梯度对状态的积分

式中，积分上限X是状态空间的一点（x₁，x₂，…，x_n）。如果积分式（4-6-17）与积分路径无关的话，则可以简化成依次沿着各坐标轴方向积分

由场论知，积分与路径无关的式（4-6-18）成立的条件是V（X）为保守场，V（X）梯度的n维旋度为零，即rot（gradV）=0。而rot（gradV）=0的充要条件是gradV的雅可比矩阵是对称阵，即有

变量梯度法的计算步骤如下：

1）按式（4-6-15）设定V（X）的梯度▽V，共有n×n个未知数a_ij（i，j=1，2，…，n）。

2）按式（4-6-16）计算导数V̇（X），限定V̇（X）负定或负半定，确定▽V中部分系数。

3）按式（4-6-19）所构成的n（n-1）/2个旋度方程，确定▽V中部分系数间的关系。

4）按式（4-6-18）计算李雅普诺夫函数V（X），限制V（X）正定，确定▽V中剩余系数。

5）最后，再确定渐近稳定的范围。

需要注意的是，如果使用变量梯度法求不出合适的李雅普诺夫函数V（X），并不意味着平衡态是不稳定的。