最直接的方法是求出系统特征矩阵的特征值,再由特征值判定对应系统的稳定性。求矩阵特征值最常用的MATLAB函数是eig,其调用格式为

上述几类反馈系统稳定性判定程序见例4-4。
【例4-4】连续状态空间系统稳定性判定的MATLAB程序。


某次运行结果如下:
特征值

稳定性判定结论
开环系统最大特征根的实部小于0,开环系统稳定!
输出反馈系统最大特征根的实部小于0,输出反馈系统稳定!
状态反馈系统最大特征根的实部小于0,状态反馈系统稳定!
输出内反馈系统最大特征根实部不小于0,输出内反馈系统不稳定!
再次运行结果为
特征值

稳定性判定结论
开环系统最大特征根实部不小于0,开环系统不稳定!
输出反馈系统最大特征根实部不小于0,输出系统不稳定!
状态反馈系统最大特征根实部不小于0,状态反馈系统不稳定!
输出内反馈系统最大特征根的实部小于0,输出内反馈系统稳定!(https://www.xing528.com)
本例程序首先设定状态空间模型阶数n,输出数p和输入数m,然后随机生成状态空间∑(A,B,C,D)的各个系数矩阵,输出反馈系数矩阵Hy,状态反馈系数矩阵Hx和输出内反馈系数矩阵Hn。再按照上节相关公式构造各种反馈连接的特征矩阵,并且求出对应的特征值。如果最大的特征根实部小于0,必然全部特征根均具有负实部,系统稳定;如果最大的特征根实部不小于0,即使其余特征根实部均小于0,也不满足所有特征根都具有负实部的条件,可以判断系统不稳定。由于系统生成,反馈系数矩阵获取均采用随机方式,所以各种反馈情况下稳定性也是随机的。参见所给出的2种运行结果可见一斑。
状态空间模型不同反馈连接的稳定性判别仿真仪见例4-5。
【例4-5】连续状态空间模型稳定性判别仿真分析仪。
连续状态空间模型稳定性判别仿真仪程序如shixz04_05所示,程序面板如图4-5-6所示,前面板如图4-5-7和图4-5-8所示,分别示出了两次随机运行结果。
程序说明:
程序的MATLAB语句见例4-4的说明和注释。系统阶次、输出和输入数由用户在n,p,m数组内设定,建议用户输入正整数。
使用char函数显示稳定性判别结果的语句如下(以开环系统稳定性判别为例):



图4-5-6 程序shixz04_05框图面板
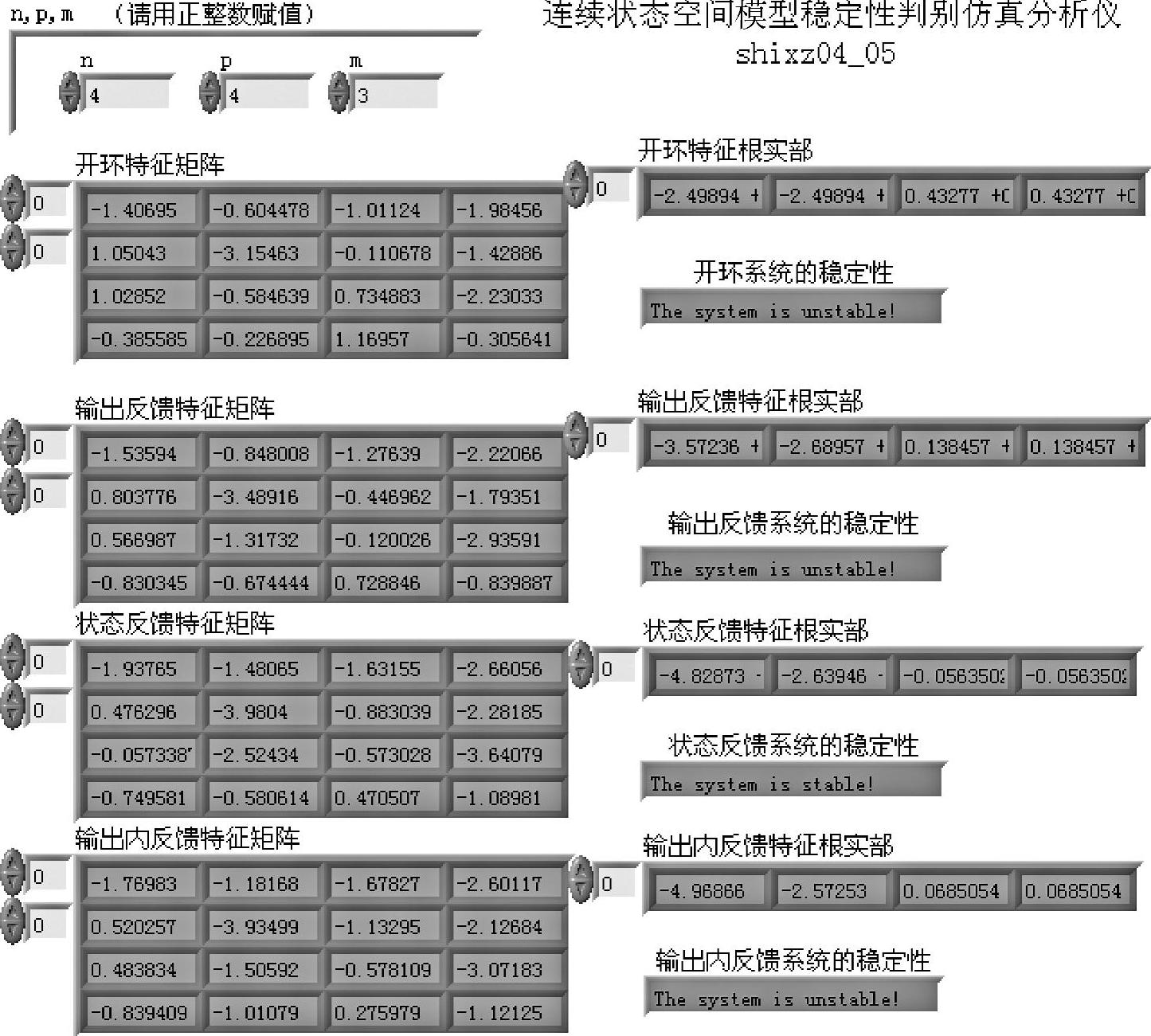
图4-5-7 程序shixz04_05前面板(状态反馈系统稳定)
稳定性判别结果信息′The system is stable!′和′The system is not stable!′由LabVIEW的字符串显示节点显示,置于相应反馈系统特征根的下面。
例4-4和例4-5的程序都只给出了各种反馈连接之下的闭环特征矩阵。请读者自己构造对应的闭环输入矩阵、输出矩阵和直传矩阵及其闭环状态空间模型,再通过impulse函数研究其单位脉冲响应,从时域响应角度研究系统的稳定性。
手动设置系统参数及反馈参数的仿真仪程序如shixz04_05a和shixz04_05b所示。用户赋值时要注意各系数矩阵的相容性。
离散状态空间模型稳定性判别仿真仪程序如shixz04_05c和shixz04_05d所示。程序的基本结构与连续系统类似,但判据不同。在离散系统中,通过判断其系统特征根是否处于单位圆内来判别其稳定性。使用了求绝对值函数abs。判别条件更改为

程序shixz04_05c由计算机随机赋值,shixz04_05d由用户手动赋值。
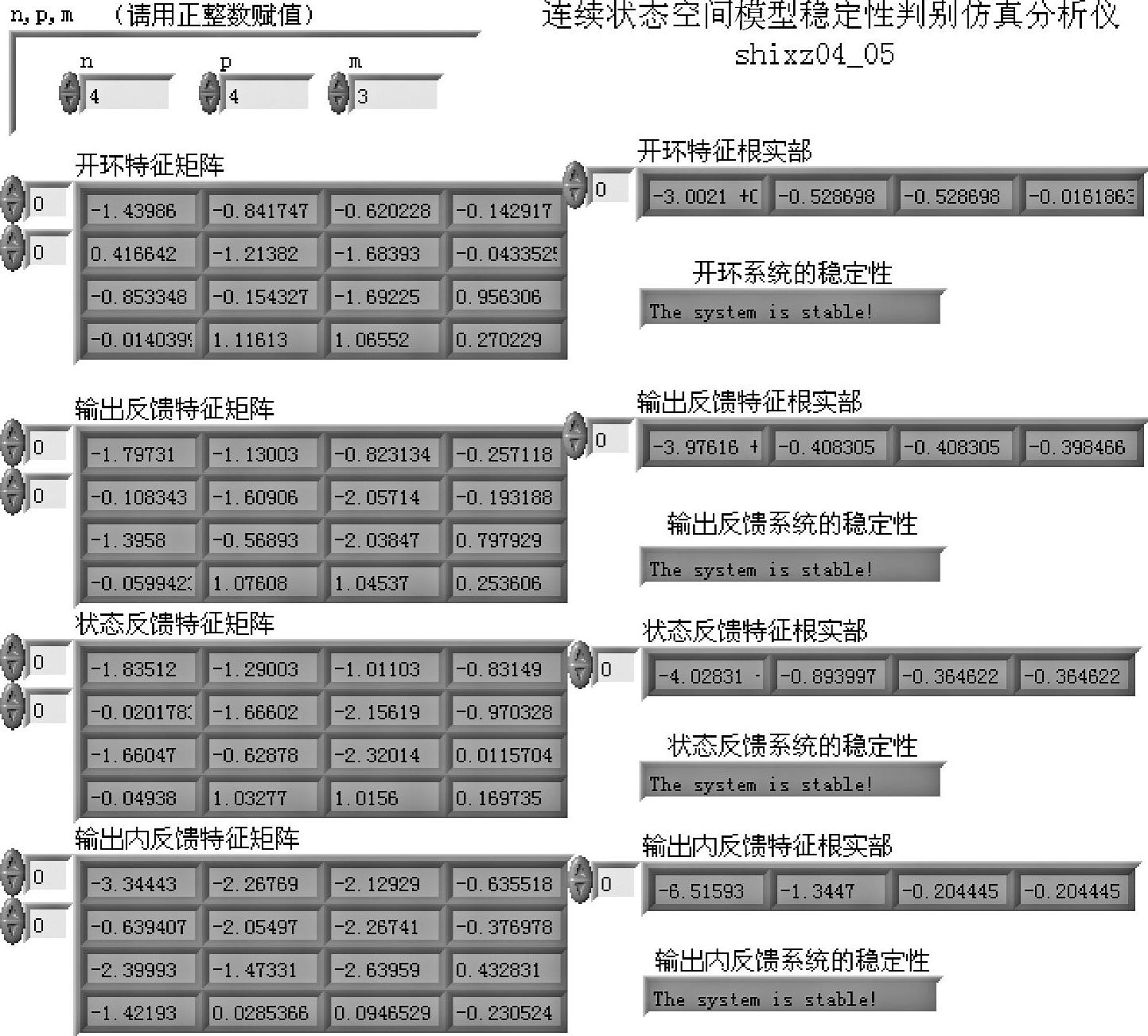
图4-5-8 程序shixz04_05前面板(全部稳定)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




