状态空间模型的开环闭环结构以及稳定性判别

连续线性定常状态空间模型稳定的充要条件是其特征方程的所有根都具有负实部，而离散状态空间模型稳定的充要条件是其所有特征根的模都小于1。状态空间模型不同的连接具有不同的特征方程形式。如果系统的输入u（t）不是状态变量X（t）或输出变量Y（t）的函数，则状态空间模型是开环的，否则系统是闭环的。对于闭环状态空间模型，由于其反馈方式不同，系统闭环的形式不同，其特征矩阵和特征方程的形式也有区别。本节仅限于讨论线性定常系统状态空间模型中反馈系数为常值阵的情况。同时，假定下述的各种反馈都可以实现。下面分别介绍状态空间模型的开环与几种闭环结构稳定性的判定。

1.开环状态空间模型的稳定性判定

为方便，重写连续状态方程见式（4-5-1），其结构图如图4-5-1所示。

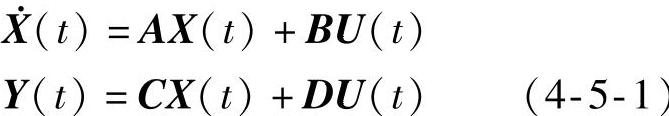
式中A、B、C、D分别为n×n、n×m、p×n、p×m维常值阵。由于输入U（t）不是X（t）或Y（t）的函数，所以系统是开环的。

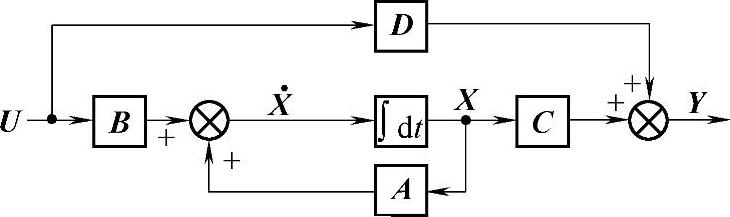
图4-5-1 连续状态空间模型的框图

系统式（4-5-1）的特征矩阵为A，特征方程为

∣λI-A∣=0 （4-5-2）

若特征方程式（4-5-2）的所有特征根都具有负实部，则开环系统式（4-5-1）稳定。

类似的，离散线性定常系统的状态方程见式（4-5-3），框图如图4-5-2所示。

X（kT+T）=FX（kT）+GU（kT）

Y（kT）=CX（kT）+DU（kT） （4-5-3）

式中，F、G分别为n×n、n×m维。

系统（4-5-3）的特征矩阵为F，特征方程为

∣λI-F∣=0 （4-5-4）

若特征方程式（4-5-4）的所有特征根的模均小于1，则开环系统式（4-5-3）稳定。

2.输出反馈状态空间模型的稳定性判定

状态空间模型输出反馈框图如图4-5-3所示。

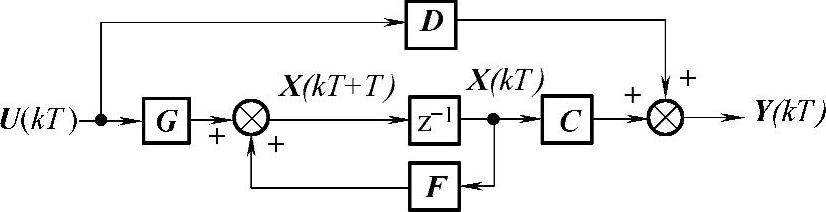
图4-5-2 离散状态空间模型框图

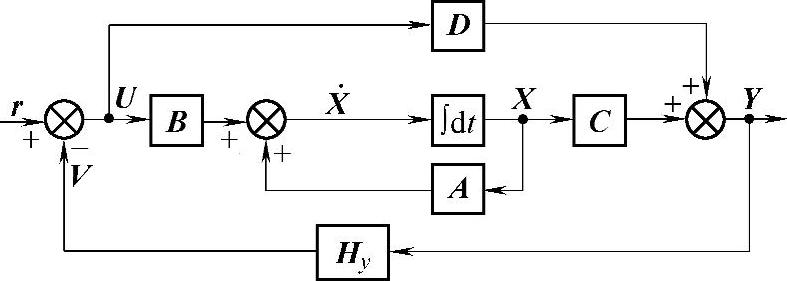
图4-5-3 输出反馈框图

由框图4-5-3有输出反馈律

U=r-H_yY （4-5-5）

式中，r为与U同维的参考输入，H_y为m×p维常值反馈矩阵。将其代入式（4-5-1）的输出方程，化简可得输出反馈后系统的输出方程

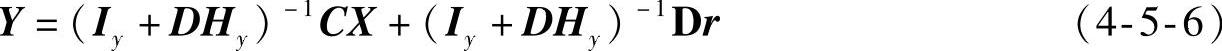
式中，I_y是p维单位阵。再将式（4-5-5）和式（4-5-6）代入式（4-5-1）的状态方程，化简后可得输出反馈后系统的状态方程

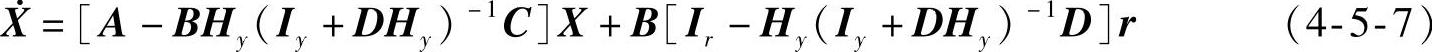
式中，I_r是m维单位阵。式（4-5-7）和式（4-5-6）一起构成输出反馈的动态方程。

输出反馈的系统矩阵为[A-BH_y（I_y+DH_y）^-1C]，特征方程为

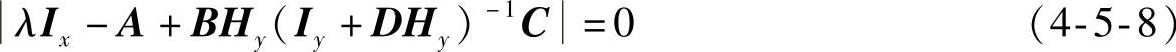
式中，I_x为n维单位阵。当直传矩阵D=0时，输出反馈系统的特征方程简化为(www.xing528.com)

∣λI_x-A+BH_yC∣=0 （4-5-9）

当特征方程式（4-5-8）或式（4-5-9）的所有根都具有负实部时，连续输出反馈闭环系统稳定。

按照同样的方式，可以得到离散系统式（4-5-3）的输入反馈的特征方程为

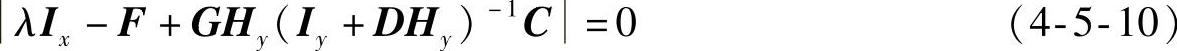
及

∣λI_x-F+GH_yC∣=0 （4-5-11）当方程式（4-5-10）或式（4-5-11）所有根的模都小于1时，离散输出反馈系统稳定。

3.状态反馈系统稳定性判定

状态反馈框图如图4-5-4所示。

状态反馈律

U=r-H_xX （4-5-12）

式中，H_x为m×n维常值状态反馈矩阵。将其代入式（4-5-1）之中，化简可得状态反馈后系统的动态方程

状态反馈的特征矩阵为（A-BH_x），特征方程为

∣λI_x-A+BH_x∣=0 （4-5-14）

如果特征方程式（4-5-14）的所有根均具有负实部，则状态反馈闭环系统稳定。显然，状态反馈的直传矩阵D只对输出方程有影响，而对状态方程没有影响。

4.输出内反馈系统稳定性判定

输出内反馈是从输出到状态微分的反馈，如图4-5-5所示。

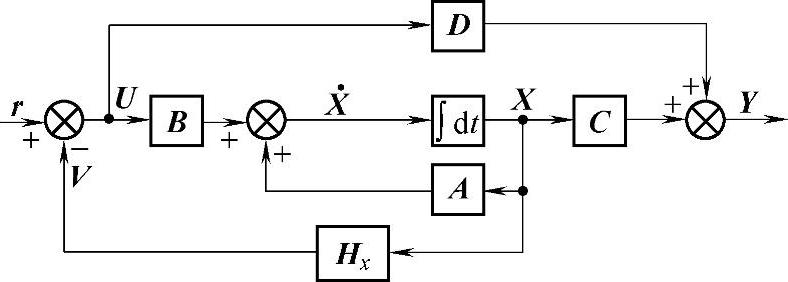
图4-5-4 状态反馈框图

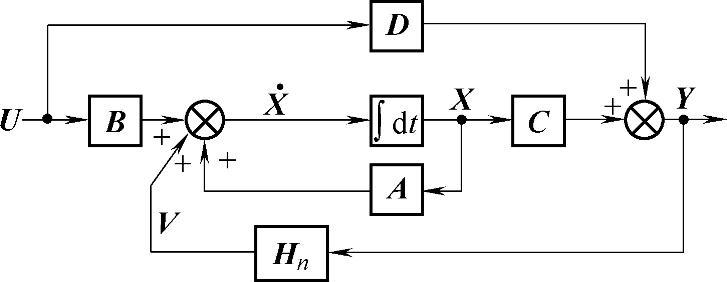
图4-5-5 输出内反馈框图

由输出内反馈框图可得（注意反馈处的符号为正号）

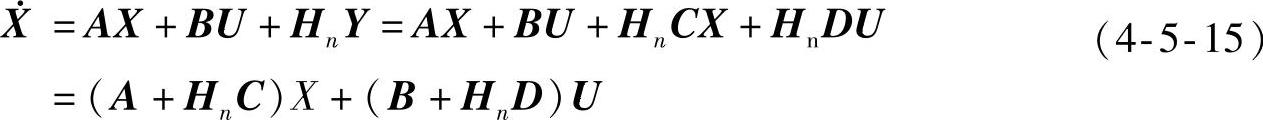
式中，H_n为n×p维常值输出内反馈矩阵。输出内反馈的特征矩阵为（A+H_nC），特征方程为

∣λI_x-A-H_nC∣=0 （4-5-16）

当特征方程式（4-5-16）的所有根均具有负实部时，由图4-5-5所描述的输出内反馈系统稳定。

用类似的方法可以获得离散状态反馈和离散状态内反馈的相应闭环特征方程及其稳定性条件。

离散状态反馈系统的特征矩阵为（F-GH_x），特征方程为

∣λI_x-F+GH_x∣=0 （4-5-17）

离散输出内反馈系统的特征矩阵为（F+H_nC），特征方程为

∣λI_x-F-H_nC∣=0 （4-5-18）

当方程式（4-5-17）和式（4-5-18）所有根的模都小于1时，相应的离散闭环系统稳定。