离散系统的频率特性可以分为真实频率特性和虚拟频率特性两种描述方法。
(1)真实频率特性描述
令
z=ejωT (4-4-2)
并使

获得离散系统的真实频率特性G(ejωT)。G(ejωT)具有连续系统中与G(jω)相同的特性。频率ω具有真实的物理意义。
(2)虚拟频率特性描述
令通过双线性变换的式(4-4-1)所获得的传递函数G(w)中的自变量
w=jv (4-4-4)
并使
G(w)∣w=jv=G(jv) (4-4-5)获得的频率特性G(jv)只有数学意义,虚拟频率v没有真实的物理意义。
过去由于运算工具的限制,较少使用真实频率特性式(4-4-3)来研究离散系统的频率特性。计算机技术的发展,为使用真实频率特性研究离散控制系统提供了良好的条件。
在MATLAB中,使用真实频率特性仿真通常采用符号函数syms,获得频率特性、实频和虚频特性、幅频和相频特性等符号表达式之后,再使用subs函数代入频率数值,绘制离散系统的奈奎斯特图和伯德图,然后使用连续系统中的奈奎斯特判据和伯德判据判定离散系统G(z)的稳定性。
使用虚拟频率特性仿真,通常在数值域内使用命令tf、zpk等获得离散传递函数G(z)、G(w)之后,再使用频域稳定性判据判断稳定性。关键语句如下:

获得G(w)后,直接绘制频率特性图。真实频率特性和虚拟频率特性两种方法的结果是一致的。
【例4-3】离散控制系统稳定性判别仿真分析仪。
离散控制系统稳定性判别仿真分析仪程序如shixz04_03所示。其程序框图面板和前面板分别如图4-4-1和图4-4-2所示。
赋值:直接在前面板“g0离散开环传递函数符号表达式”框内输入仿真对象的Z传递函数g0。示例的离散开环传递函数g0为
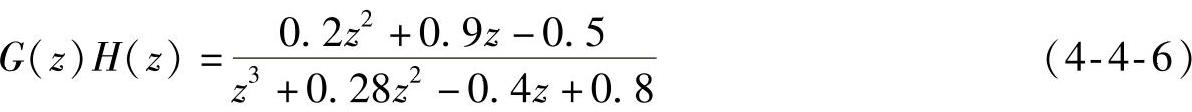
当然,读者可以任意输入其他离散开环传递函数的符号表达式。
程序结构与例4-2类似,参见图4-4-1和图4-4-2。下面仅就不同之处进行说明。
仿真仪使用真实频率特性和虚拟频率特性两种方法绘制仿真系统的奈奎斯特图。真实频率特性的相关语句如下:(https://www.xing528.com)

reg和img不一定是最简表达式,但不影响后面的数值计算。将reg和img数值化:

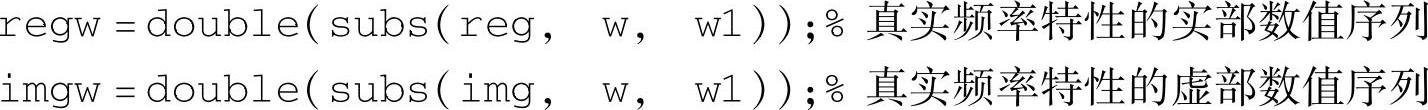
利用regw和imgw即可作出真实频率特性描述法的奈奎斯特图。
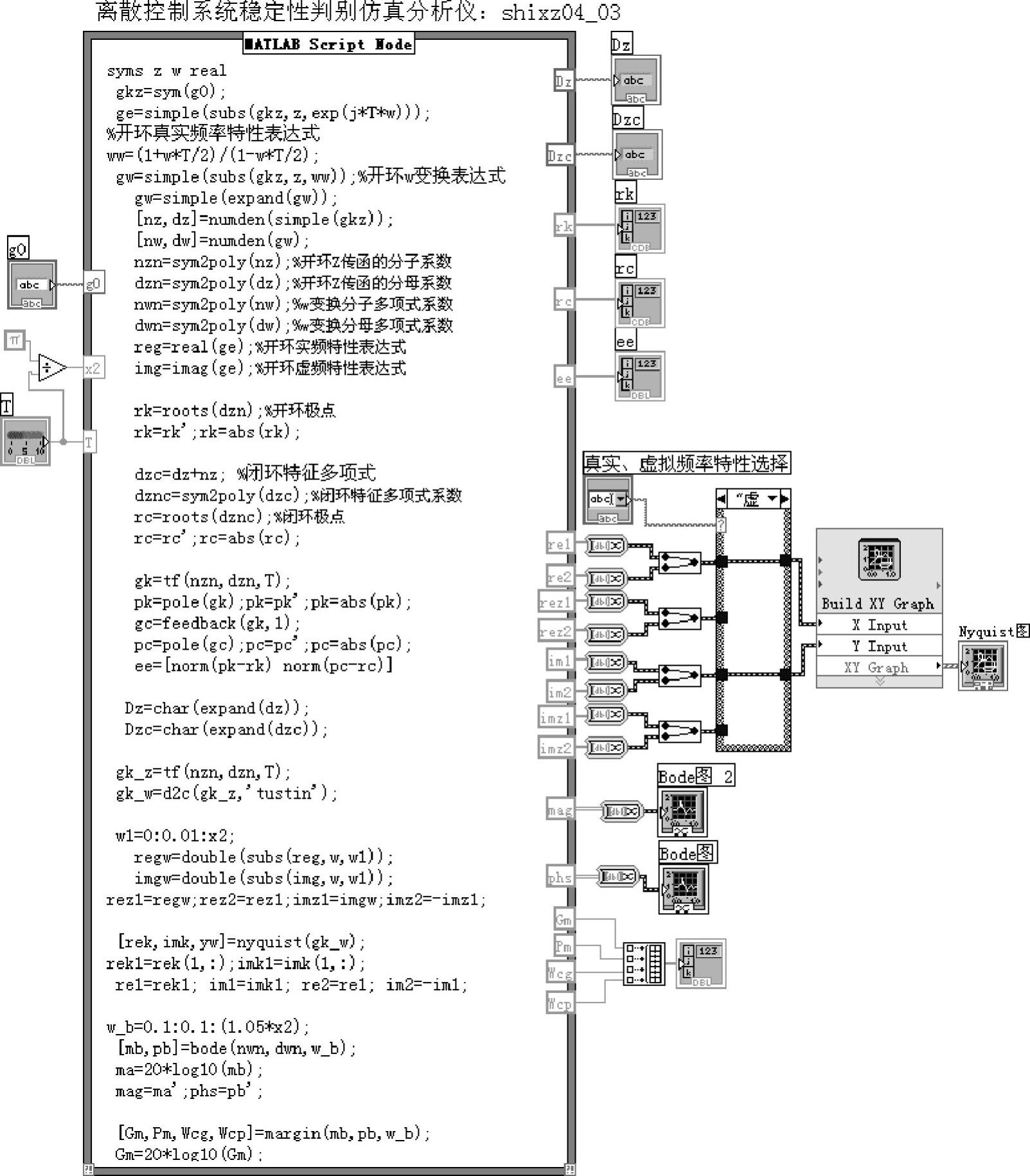
图4-4-1 程序shixz04_03框图面板
虚拟频率特性描述法的主要语句如下:
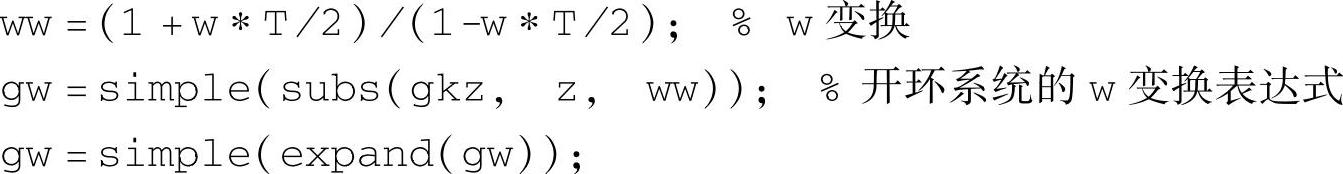

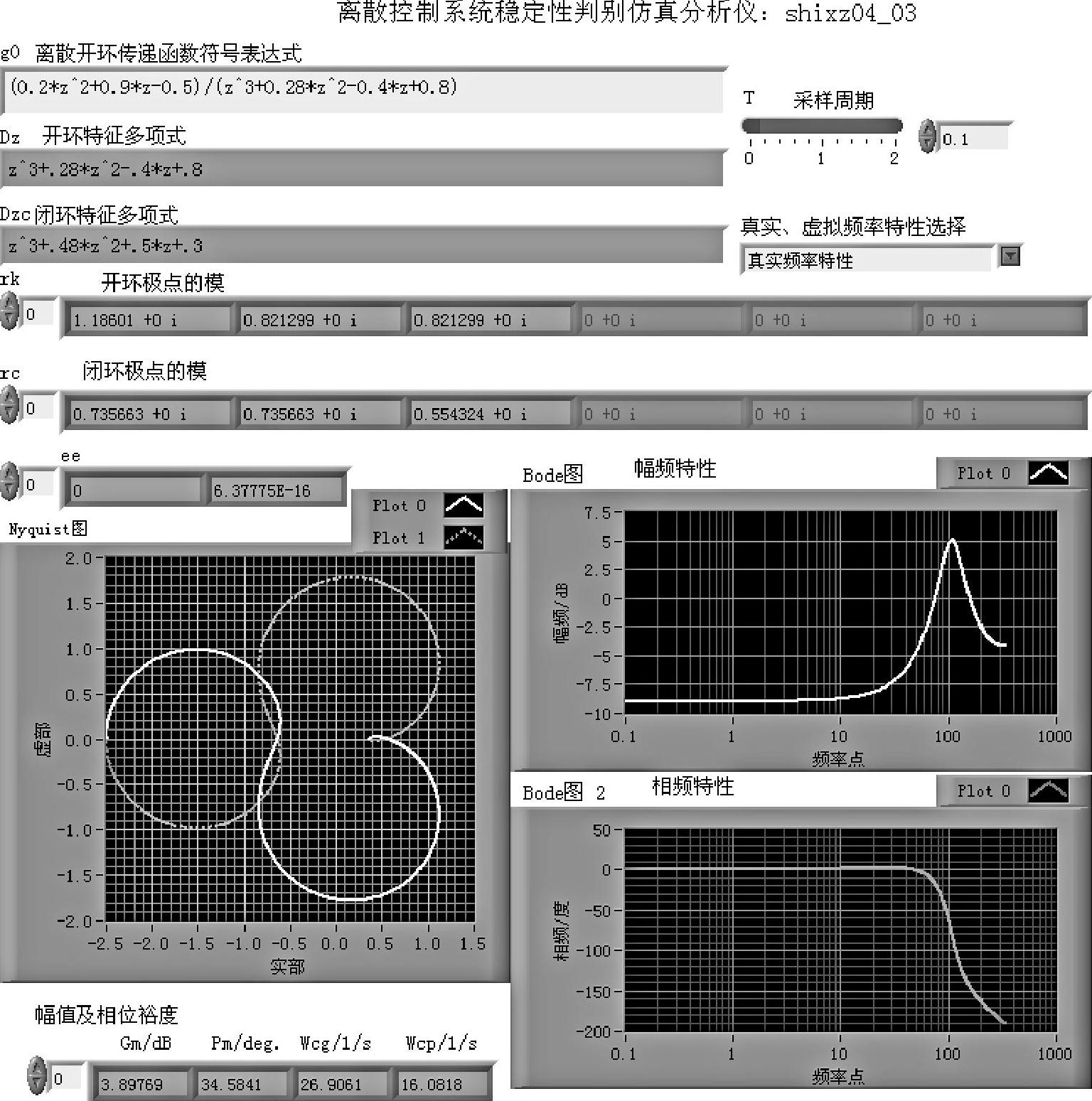
图4-4-2 程序shixz04_03前面板
利用w变换后传递函数分子分母系数nwn和dwn可以方便地作出奈奎斯特图与伯德图。
根据采样定理,离散系统频率不得超过采样频率的二分之一,所以仿真频率的上限x2被限制在π/T之内。为了使伯德图的相频特性能够超过-180o,绘制伯德图时频率上限x2可以略大于π/T。图示仪实例上限x2取为1.05(π/T)。
参见图4-4-2,实例有1个开环极点处于单位圆外,开环系统不稳定。而所有闭环极点的模全部小于1,全部处于单位圆内,所以闭环系统稳定。由开环系统的奈奎斯特图可见,开环奈奎斯特轨迹逆时针围绕[W]平面(-1,j0)点1圈(见图4-4-3),也说明其对应的单位反馈系统稳定。前面板设置了如图4-4-4所示的选择开关,供选择“真实频率特性”或“虚拟频率特性”两种描述方法。两种奈奎斯特图的转换由选择结构实现,如图4-4-5所示。仿真表明,二者结果相同。
仿真系统的伯德图如图4-4-2所示。幅值及相位裕度示于图4-4-2的左下方,它们都具有正值,由伯德判据也可获得闭环系统稳定的结论。
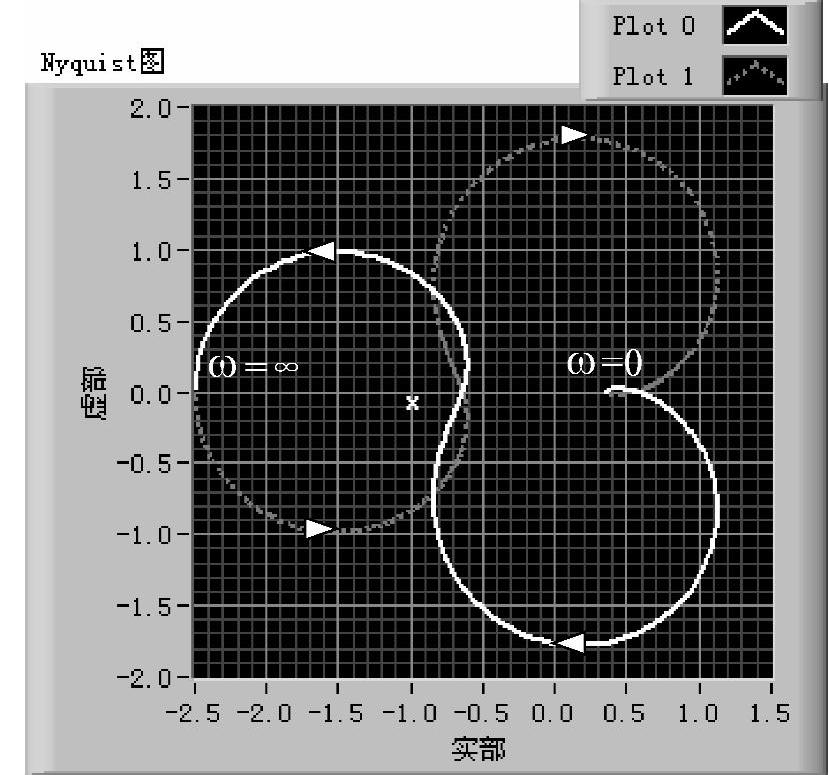
图4-4-3 离散系统式(4-4-6)的奈奎斯特图
图4-4-4 真实、虚拟频率特性选择开关
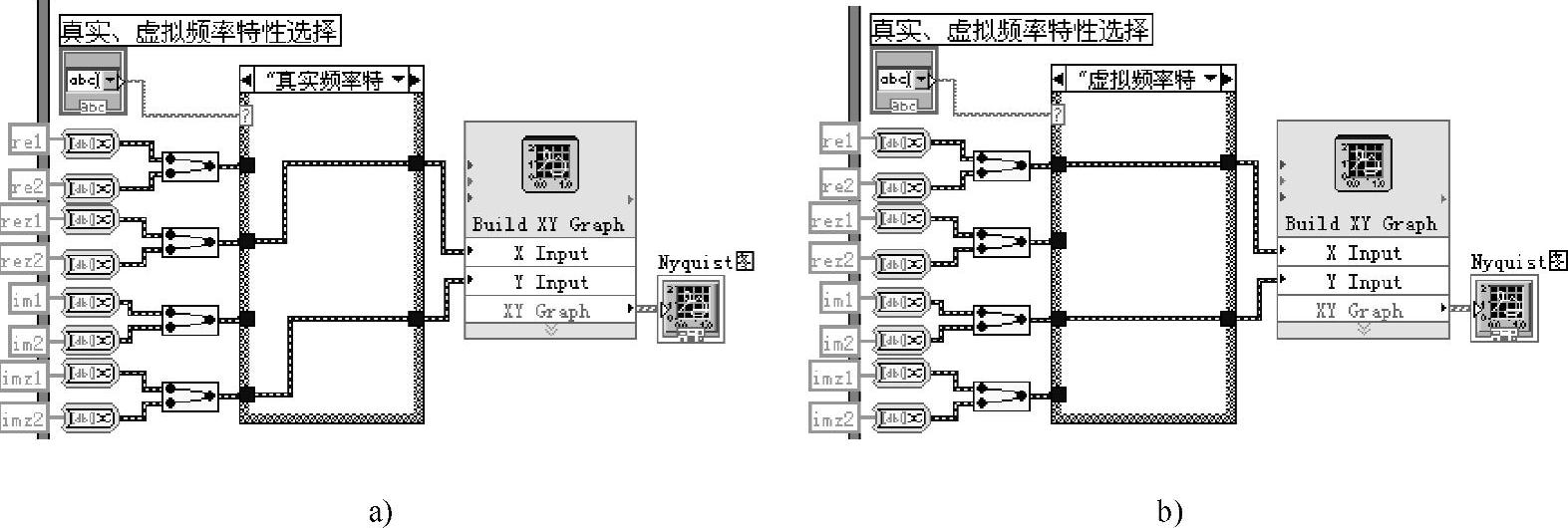
图4-4-5 奈奎斯特图的显示选择结构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




