连续控制系统稳定性判定及仿真优化

连续控制系统的稳定性判别最直接的方法是求出系统特征方程的数值根，常用MATLAB命令如下：

使用上述命令求出特征根（极点）后，再考查特征根是否具有负实部以判断连续系统的稳定性。使用上述命令时，必须首先求出需要判断稳定性的系统sys，对于一个复杂系统常常需要预先进行串联、并联、反馈等连接变换。

使用符号工具箱的syms或sym及其四则运算函数可以方便地求出系统传递函数的符号表达式，再通过numden和sym2poly函数可以求出传递函数分子分母符号多项式及其系数，再使用求特征根的命令求出传递函数的极点。

numden的调用格式为

sym2poly的调用格式为

【例4-1】判断开环传递函数式（4-3-1）及其单位反馈系统的稳定性。

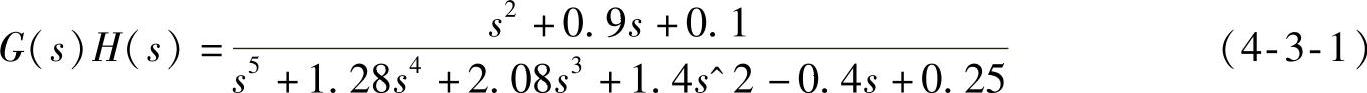
参考程序如下：

运行该程序，分别得到开环极点rk及闭环极点rc如下。

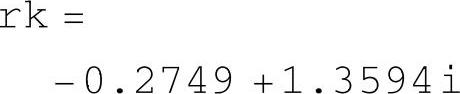
显然，该系统开环不稳定，闭环稳定。

实际上，由劳斯判据的必要条件，直接观察式（4-3-1）可立即判定开环系统不稳定，因为其特征多项式系数不同号。作为检验，读者还可以紧接上段程序使用其他命令计算极点。例如运行程序

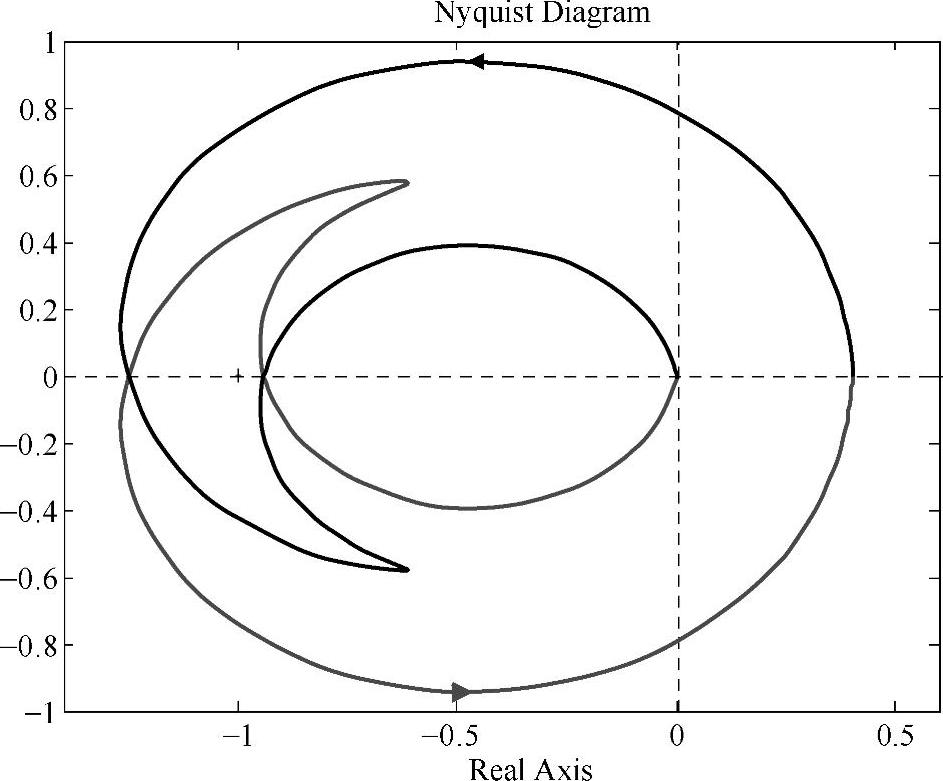
图4-3-1 式（4-1-1）的奈奎斯特图

绘出开环系统式（4-3-1）的奈奎斯特图和伯德图，如图4-3-1和图4-3-2所示。从图4-3-1可见，当频率ω从-∞到+∞变化时，开环系统的奈奎斯特图逆时针围绕（-1，j0）点2圈，由于该开环系统式（4-2-4）在[S]右半平面系统有2个极点（见rk），所以对应闭环系统稳定。从图4-3-2可见，系统有正的相位和幅值裕度，也可判断其闭环系统稳定。

【例4-2】连续控制系统稳定性判别仿真分析仪。(www.xing528.com)

连续控制系统稳定性判别仿真图示仪程序如shixz04_02所示，其程序框图面板和前面板分别如图4-3-3和图4-3-4所示。

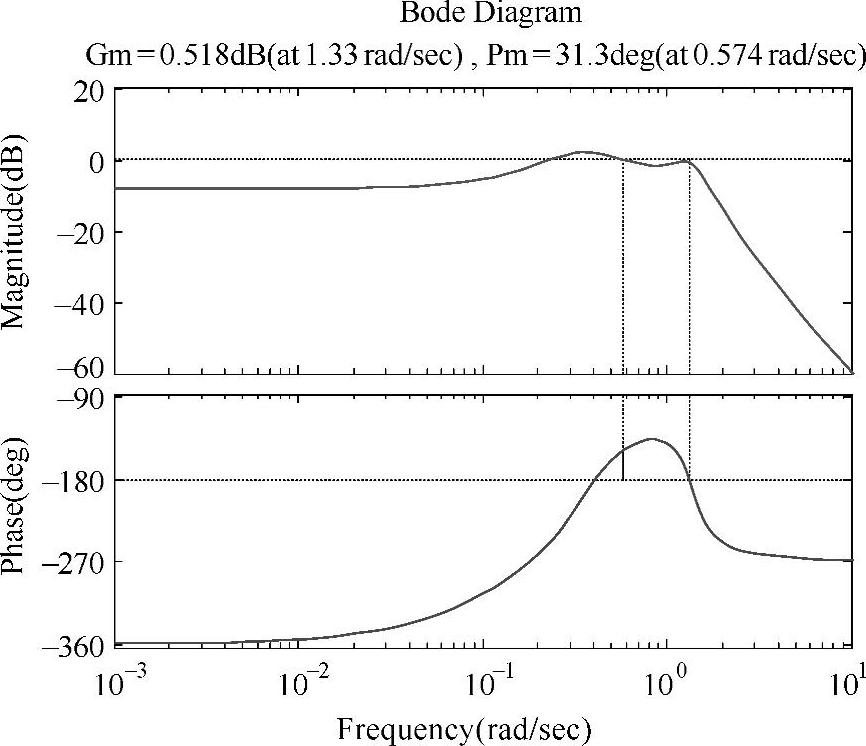
图4-3-2 式（4-1-1）的伯德图

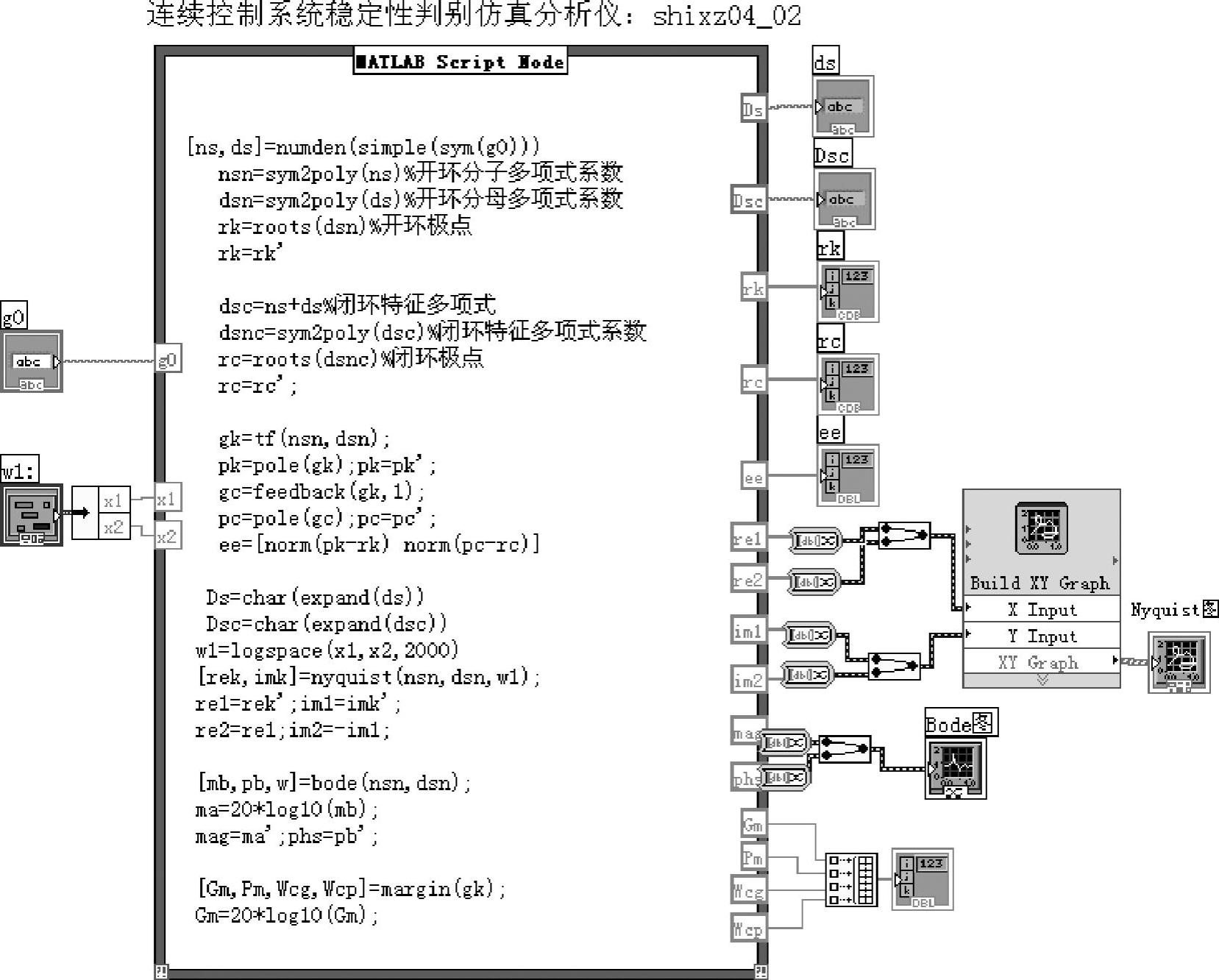
图4-3-3 程序shixz04_02框图面板

程序说明：

该仿真仪可以判断开环系统及其对应的单位反馈闭环系统的稳定性。

赋值：直接在前面板“g0输入开环传递函数的符号表达式”框内输入待仿真对象的符号表达式。示例的开环传递函数为

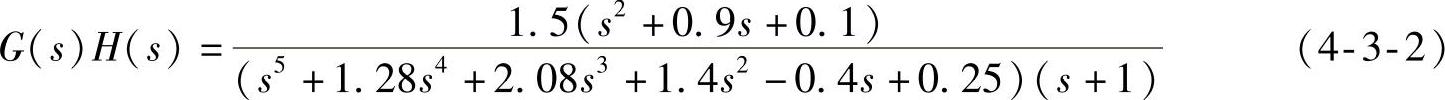
当然，读者可以任意输入其他开环传递函数。

程序结构：

参见图4-3-3和图4-3-4。程序包括传递函数的符号表达及数值转换，系统特性的数值计算和数值与图形显示3个部分。

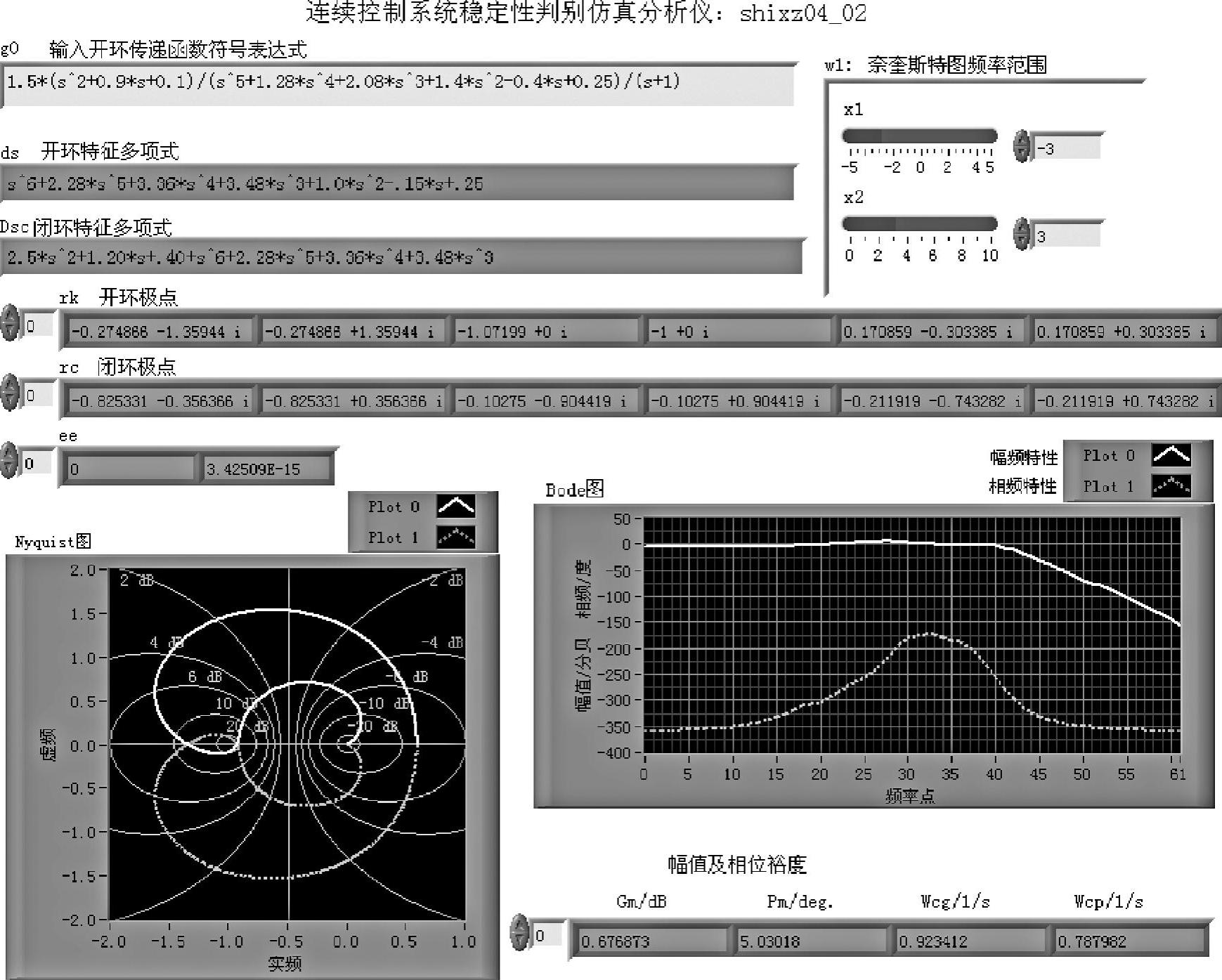
图4-3-4 程序shixz04_02前面板

前面板输入的符号表达式传递函数由LabVIEW中的字符串控制（String Control）节点输入到MATLAB脚本节点。在MATLAB脚本节点内调用符号工具箱中的sym函数后再使用numden命令获取传递函数的分子、分母多项式。该语句是本程序的关键语句，摘录如下：

sym2poly命令提取传递函数分子和分母多项式系数，再构造单位反馈闭环系统，使用roots命令分别求出开、闭环特征根rk和rc，并返回到前面板，供查看是否含有非负实部根，从而判断系统稳定与否。参见图4-3-4，示例数组rk内有2个非负实部根，说明开环系统不稳定；而数组rc内没有非负实部根，说明闭环系统稳定。程序还使用了命令pole求开环、闭环极点，二者的比较示于数组ee之中。

作为对比，程序还给出了开环系统的奈奎斯特图和伯德图。当频率从-∞到+∞变化时，奈奎斯特曲线逆时针围绕（-1，j0）点2圈，由奈奎斯特稳定性判据也可得出闭环系统稳定的结论。开环系统伯德图显示，开环系统具有正幅值裕度和正相位裕度，幅值和相位裕度及其对应的穿越频率示于前面板右下方的“幅值及相位裕度”数组内。

为了清晰作出Ⅰ型或Ⅱ型系统的奈奎斯特图，图示仪提供了“w1：奈奎斯特图频率范围”簇供用户设置，其中的x1和x2分别表示奈奎斯特曲线起始频率与终止频率的对数值。注意伯德图的调用格式采用[mb，pb，w]=bode（nsn，dsn）。仿真表明，这种格式可以保证相频序列pb在大滞后情况下的正确表达，在LabVIEW中绘制高阶系统的伯德图时更要注意。

对于非单位反馈的闭环系统，稳定性判别程序如shixz04_02a所示。