多输入多输出系统的频率特性仿真实例

对于多输入多输出系统，各种频率特性曲线都是针对传递函数矩阵中的各个传递函数作出的。对每个传递函数而言，实际上是一个单输入单输出系统。

【例3-2】多输入多输出系统频率特性仿真分析仪。

以三阶三输出二输入系统为例，其频率特性仿真程序如shixz03_02所示。仿真程序的前面板和程序框图面板如图3-4-5和图3-4-6所示。

图3-4-5 程序shixz03_02前面板

程序说明：

由于本例是一个三阶三输出二输入系统，所以传递函数矩阵为三行二列，见式（1-3-15）。令该式中的s≡jω，得到如下谐波传递函数矩阵，称之为“频率特性矩阵”，见式（3-4-2）。

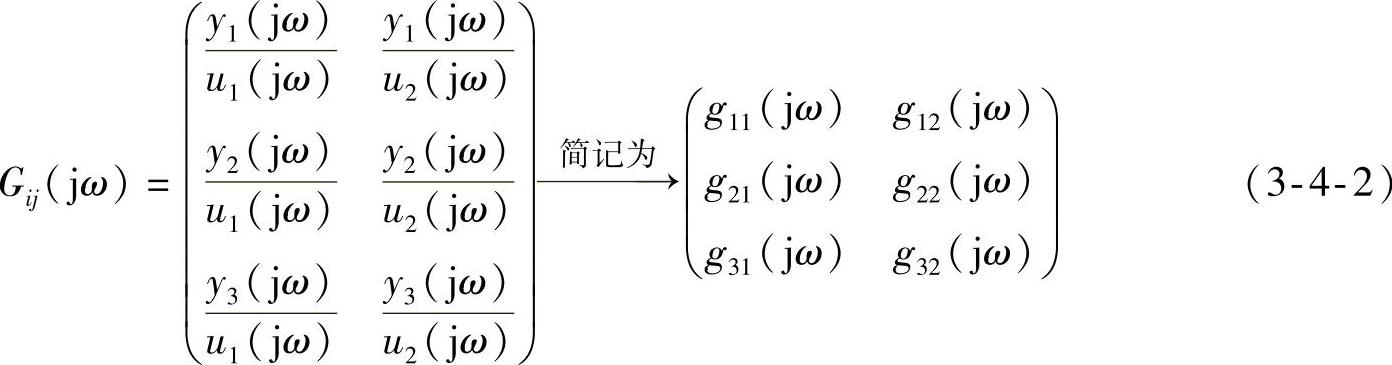
程序使用如图3-4-7所示的选择结构选择所要仿真的频率特性对象。对于每个谐波传递函数g_ji（jω）=y_j（jω）/u_i（jω）（j=1，2，3；i=1，2），分别给出其奈奎斯特图、伯德图和尼科尔斯图，如图3-4-5所示。

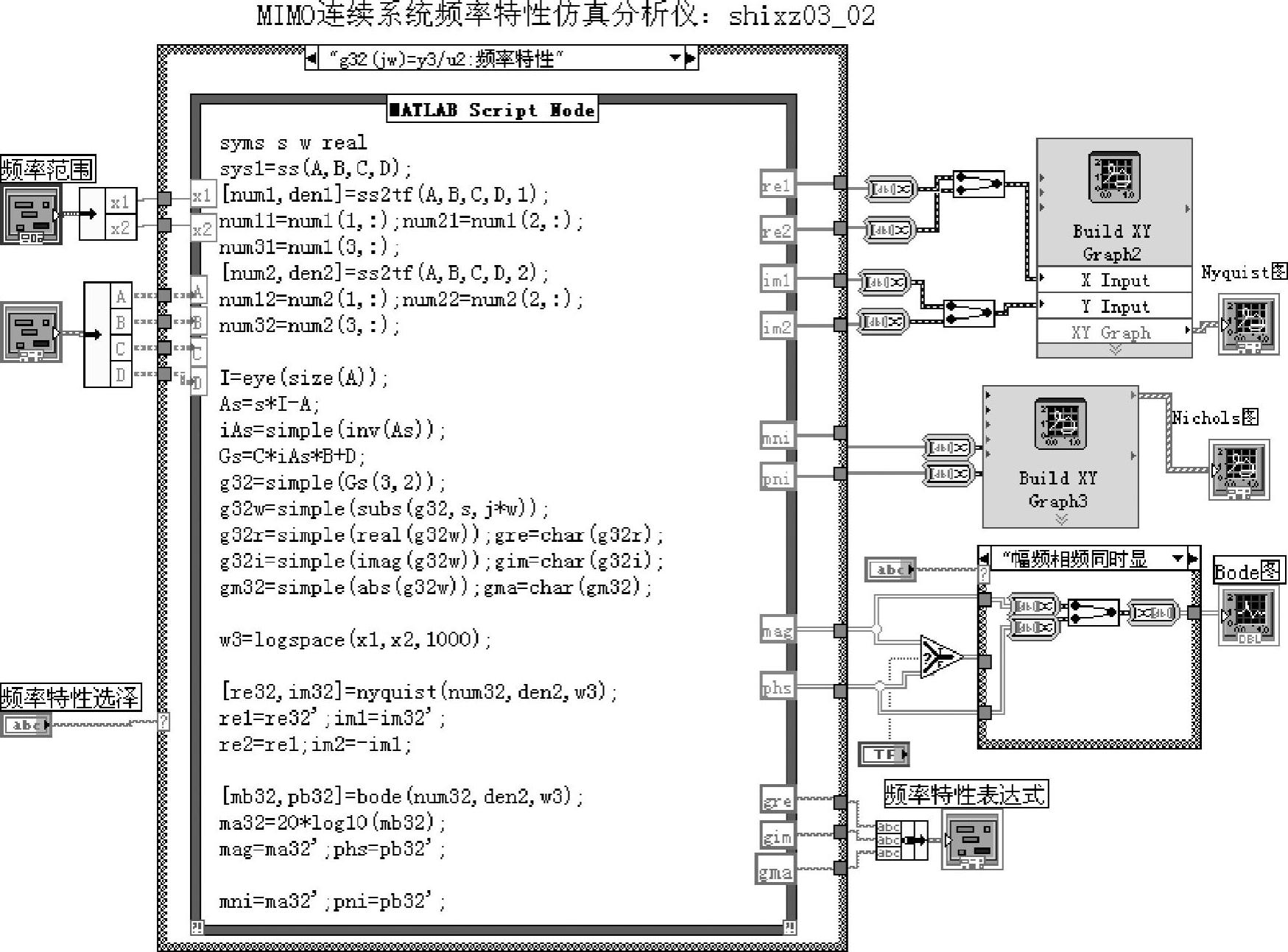
图3-4-6 程序shixz03_02框图面板(www.xing528.com)

奈奎斯特图由正负频率段的两条对称曲线构成，分别由图例的plot0和plot1表示。使用xy函数记录仪显示，编写程序时由命令[rea1，imag]=nyquist（sys，w）所获得的实部数据组合后进入x通道，虽然所组合的实部数据完全相同，但由于LabVIEW的选择结构（Case Structure）输出口（Output）不允许使用重复名称，所以程序中分别用re1和re2表示完全相同的实频特性。进入y通道的虚频特性数值相同符号相反，分别用im1和im2表示，如图3-4-6所示。

图3-4-7 频率特性选择

每个频率特性的伯德图和尼科尔斯图见前例说明。

改变系统参数A，B，C，D可以构成新的仿真对象，但本例只适用于三阶三输出二输入系统的完整仿真。同样，改变仿真频率范围，可以精细显示所关注频段的频率特性。

为了避免伯德图中相频特性的突变，程序采用ss2tf命令求出传递函数矩阵各元的多项式系数格式：

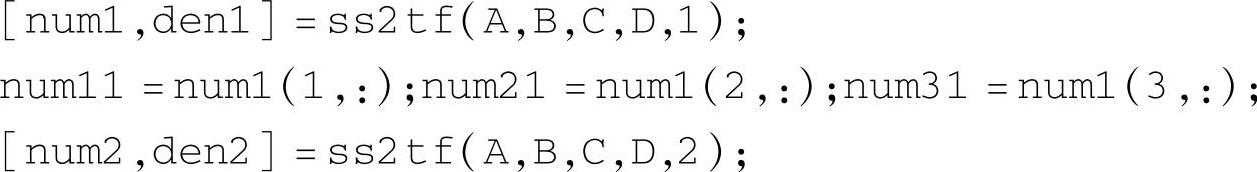
程序段中分子多项式系数的标号与式（3-4-2）中频率特性标号对应。分母多项式系数den1与den2完全相同，因为系统矩阵的特征多项式是唯一的。

与例3.1类似，尼科尔斯图的幅频特性和相频特性取自命令bode的计算结果，只是重新命名了输出通道。例如，仿真g₁₁（jω）的结构1的相应语句为mni=ma11′；pni=pb11′；等。