MATLAB求解状态方程的命令

使用MATLAB符号工具箱，可以求出比较简单（例如三阶及其以下）的状态方程解的解析式。如果只需进行数值仿真，则不受限制。由式（2-5-5）可知，获取状态方程解析解的关键在于矩阵指数的计算。

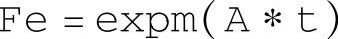
用于返回系统的状态转移矩阵。状态转移矩阵也可以使用拉普拉斯逆变换命令得到

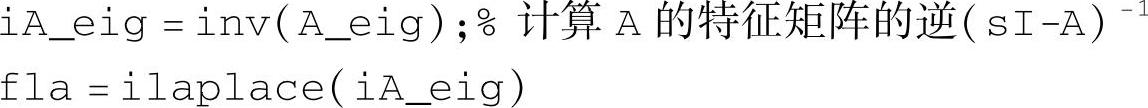
返回与命令expm（A*t）相同的结果。使用语句Xa=Fe*X0或Xa=fla*X0均可得到状态的零输入响应解析式X_a。

求系统状态的零状态响应X_b也有两种方法，一种是拉普拉斯逆变换法，主要命令有

求状态的零状态响应X_b还可以使用积分方法计算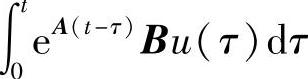，程序如下

通过零输入和零状态响应叠加可以求出完全状态响应的解析式，再通过输出方程可以求出输出响应的解析式。

由解析式可以方便地进行数值仿真。如果只需要进行数值仿真与动态曲线绘制，直接使用命令initial和lsim命令即可。详见下例。

【例2-9】状态方程解析解及其数字仿真。(www.xing528.com)

上列程序包含了如下4个部分：

①获取状态方程和输出方程解析解。

②由解析解转换成数字序列。

③直接获取状态及输出响应的数字序列。

④比较与作图。

无论是解析解还是数字解都分别包含零输入、零状态响应的状态轨迹及对应的输出响应。这些响应中包含各个分量信息。状态响应轨迹及输出响应分别如图2-5-1a，2-5-1b所示。程序中积分项语句Fe1=int（expm（A*（t-q））*B*u_2，q，0，t）是对式（2-5-5）的实现，特别注意当输入u（t）是时间的函数时，被积函数是矩阵指数、输入矩阵B和输入u（t）的乘积。

图2-5-1 三阶二输出系统状态轨迹及输出响应曲线

a）状态轨迹 b）输出响应