MATLAB高阶控制系统时域特性仿真主要命令

由上面分析可知，求取高阶系统时域特性的基本方法是进行部分分式展开，需要求出系统的极点。虽然理论上知道系统的n个极点总是存在的，但要用手工求出3阶以上系统的极点却是很难的。MATLAB提供了留数计算命令residue用于部分分式展开，调用格式为

返回3个列向量。r表示G（s）部分分式的各个系数，p表示G（s）的所有极点。r和p的数量相同并等于G（s）的阶数。重复极点分别列出，共轭极点分开列出。r（i）与p（i）互相对应。当m＜n时，k=[]（空矩阵）。

命令

将部分分式展开式转换成传递函数多项式分式系数。

【例2-8】设高阶控制系统为

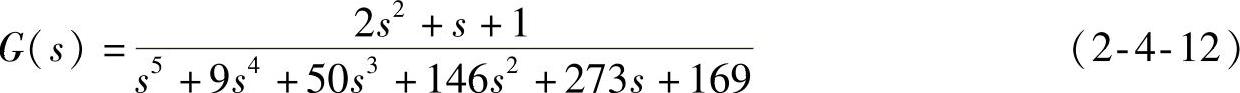
求出各子系统的表达式及其单位脉冲响应，求出系统单位脉冲响应。

程序如下：

程序运行r，p，k矢量结果为

由于有重共轭复根，在组成部分分式时系数r和极点p有确定对应关系，为此，程序对系数和极点进行了重新书写确认。仿真实践表明，重新书写r和p对表达式的化简是有益的。(www.xing528.com)

程序返回的共轭复数极点项的函数表达式

F13=（-20*s-349）/（1000*s^2+4000*s+13000）

与式（2-4-3）等价。其对应的单位脉冲响应

f13=1/1000*（-20*cos（3*t）-103*sin（3*t））/exp（t）^2

与式（2-4-10）等价。程序返回的重共轭复数极点项的函数表达式

F24=（361/1250*s^2+1847/625*s+539/250）/（s^2+4*s+13）^2

与式（2-4-7）等价。其对应的单位脉冲响应

f24=1/1250*exp（-2*t）*t*（361*cos（3*t）+375*sin（3*t））

与式（2-4-11）等价。高阶系统单位脉冲响应如图2-4-1所示。图中曲线f=f₁₃+f₂₄+f₅与直接使用命令impulse的曲线完全重合。

需要注意，命令residue在展开多重极点时，有时会出现“病态问题”，计算留数出现很大误差，甚至失败。这时使用状态空间或零极点增益模型更好。

当然，如果不需要求出组成高阶系统的各子系统，只需要求取对输入的响应，仿真时可使用前面所述的命令和方法。也就是说，仅从数字仿真而言，高阶系统与一阶、二阶系统没有区别。

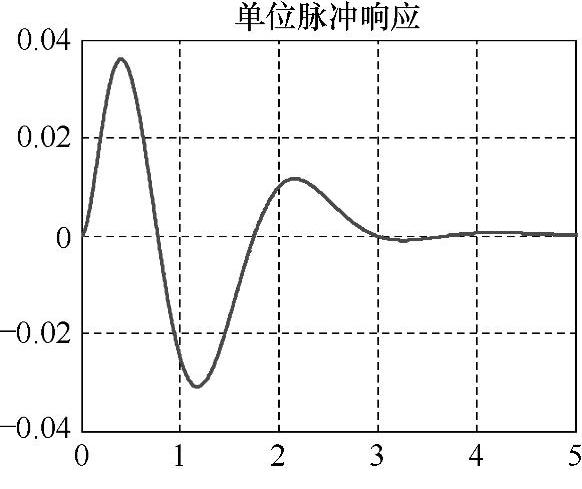
图2-4-1 高阶系统的单位脉冲响应