二阶控制系统的时域响应仿真实例

【例2-6】二阶控制系统典型输入响应仿真仪。

对式（2-3-1）的二阶控制系统典型输入响应进行仿真。仿真程序如shixz02_06所示，其程序框图面板及前面板分别如图2-3-2和图2-3-3所示。

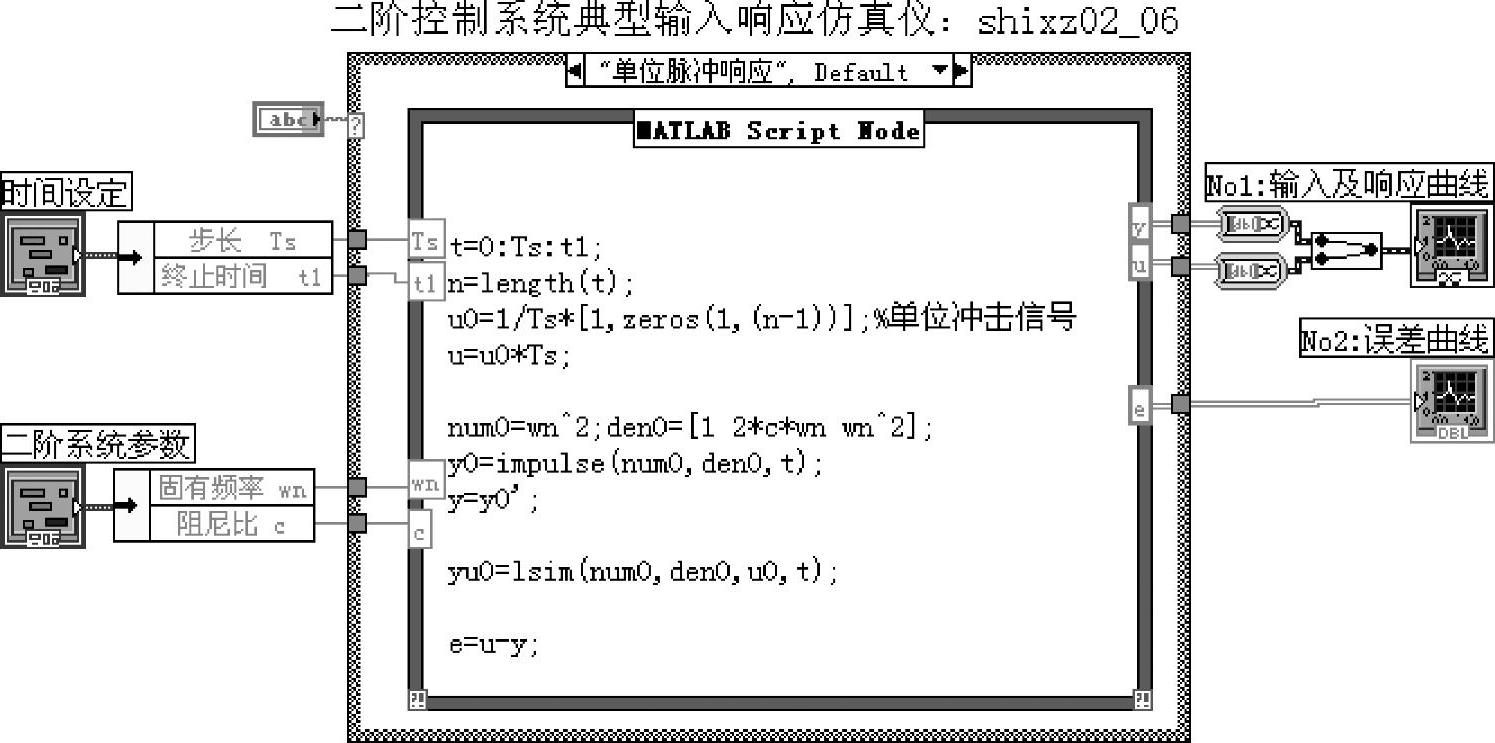
图2-3-2 程序shixz02_06框图面板

1.赋值

“时间设定”赋值框设定“步长T_s”及“终止时间t₁”两项。

“二阶系统参数”赋值框设定式（2-3-1）所示的“固有频率ω_n”及“阻尼比ξ”两项。

前面板中的输入响应选择，各示波器面板及其测量坐标等项参见一阶系统的说明（见图2-2-3），不再赘述。

2.运行程序

选择一种输入响应（默认单位脉冲响应），连续运行程序。改变系统参数，可见响应曲线和误差曲线随参数改变而同步连续改变。例如，对于单位阶跃响应，选择阻尼比ξ的值，可以实现无阻尼、欠阻尼、临界阻尼和过阻尼的仿真，可以动态显示不同阻尼比响应曲线的演变，动态显示阻尼比对系统振荡性及超调的影响。改变固有频率ω_n，响应振荡快慢发生变化，但不影响超调。测量坐标系可以测量二阶系统时域性能的各项指标数据。如在图2-3-3参数的情况下，坐标系测得单位阶跃响应的峰值时间为1.6s，峰值为1.5266，误差为-0.5266。由仿真曲线可见，二阶系统式（2-3-1）单位阶跃响应的稳态位置误差为零，单位恒速响应的稳态误差为定值2ξ/ω_n。

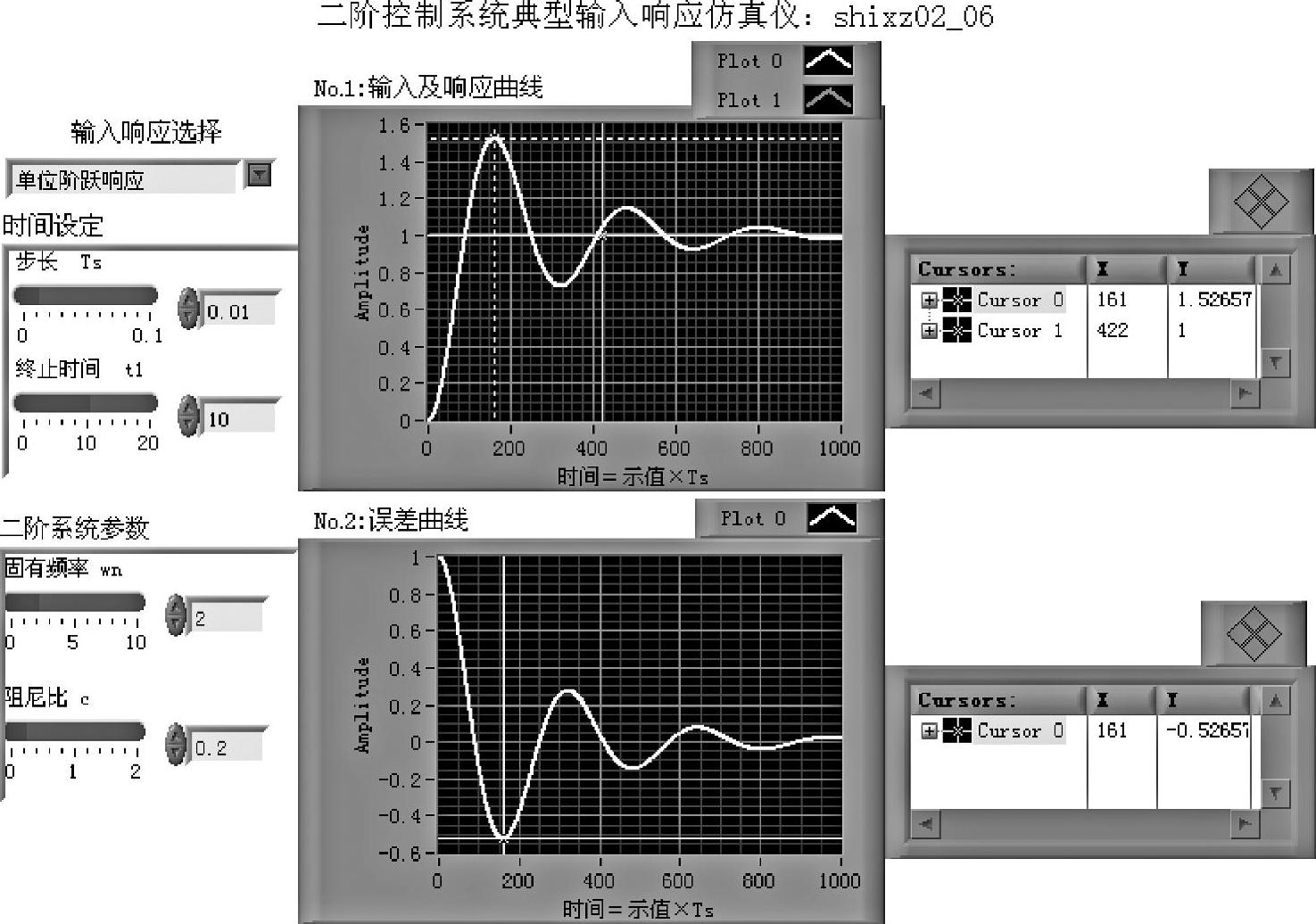
图2-3-3 程序shixz02_06前面板

二阶系统式（2-3-4）典型输入响应的仿真程序如shixz02_06所示。运行该程序，可以对比研究系统式（2-3-4）各参数对其时域性能的影响。当c=4，a=0.8，b=1时该系统单位阶跃响应如图2-3-4所示。

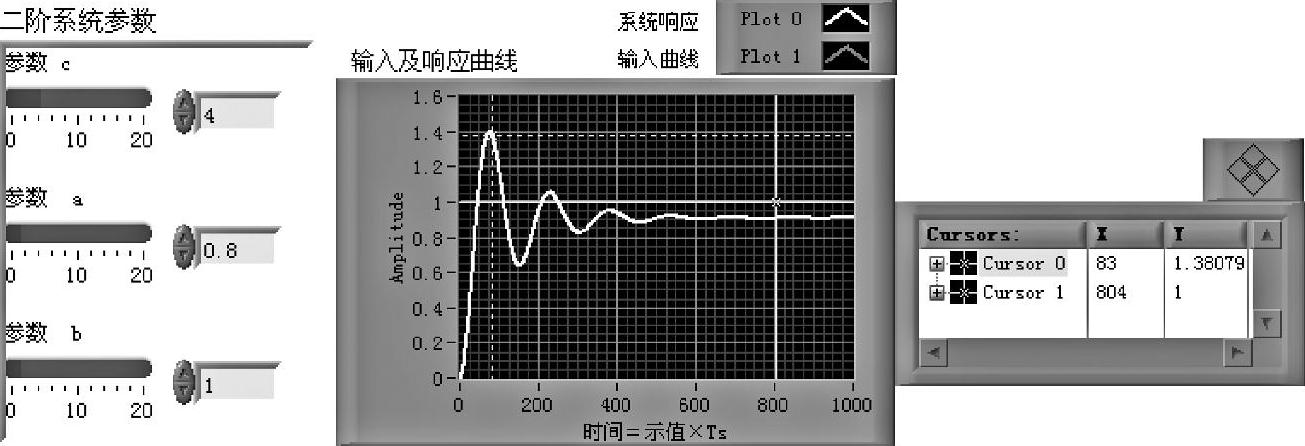
图2-3-4 二阶系统式（2-3-4）的单位阶跃响应

【例2-7】二阶控制系统的零输入、零状态响应的仿真分析仪。

如前所述，例2-6获得的是系统初始状态为0的零状态响应。下面仍以“组合”典型信号为例，讨论二阶系统的零输入、零状态响应以及系统的完全响应。仿真程序如shixz02_07所示，程序框图面板及前面板分别如图2-3-5和图2-3-6所示。

程序说明：

1.赋值

“输入”赋值。输入“组合”典型信号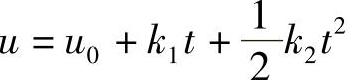，通过对初位移u₀、速度k₁、加速度k₂的赋值，设定输入为阶跃、恒速和恒加速信号

初态X₀赋值。二阶系统初态有两个分量X₀=[X₁₀；X₂₀]。由于讨论的是单输入单输出系统，为方便计算，这里的初态指的是二阶系统在t=0的输出值，而非状态值。所以在程序中已将此初始状态值转换为初始输出值。

其余各项赋值前例已有说明。

图2-3-5 程序shixz02_07框图面板

2.程序特点

仿真零输入响应、零状态响应和完全响应所用主要命令initial和lsim的调用格式和使用方法前已说明。为使初态表示初始输出，必须满足输出方程Y=CX。所仿真的二阶系统转换成状态方程后，其输出矩阵格式为C=[0，c₂]，所以在程序中实际参与运行的初态为X₀=[X₁₀；X₂₀]/C（1，2）。这样，经过输出方程运算，初始输出等于对X₀所赋的初值。如图2-3-6中，零输入响应初值等于初态X₂₀=10。

3.程序运行

如图2-3-6所示，赋值后，选择输入响应（默认零输入+零状态响应），单击单次运行或连续运行按钮，示波器面板No.1上plot0显示初态为设定值10的零输入响应曲线。plot1显示对初态为零，设定输入u=20-1.5t+（1/2）t²的响应曲线。显然二者之和（叠加）可得系统对设定输入，在设定初态下的完全响应曲线。(www.xing528.com)

示波器面板No.2上plot0为系统对设定输入，在设定初态下的完全响应曲线。plot1显示对初态为零，设定输入u=20-1.5t+（1/2）t²的响应（与“零输入与零状态响应曲线”面板上plot1相同）。plot2显示输入曲线。

如前分析，系统零输入响应是暂态响应，体现单位脉冲响应的规律。系统对输入的响应由输入规律决定，无论其初始状态如何，最终都跟踪输入变化，是强迫响应。

二阶系统对恒速输入的稳态误差为k₁（2ξ/ω_n）。图2-3-7给出了稳态误差随固有频率与阻尼比的变化情况。当输入为u=20-1.5t时，对于同一时间测量点，图2-3-7a的误差为-1.5，图2-3-7b的误差为-0.75。

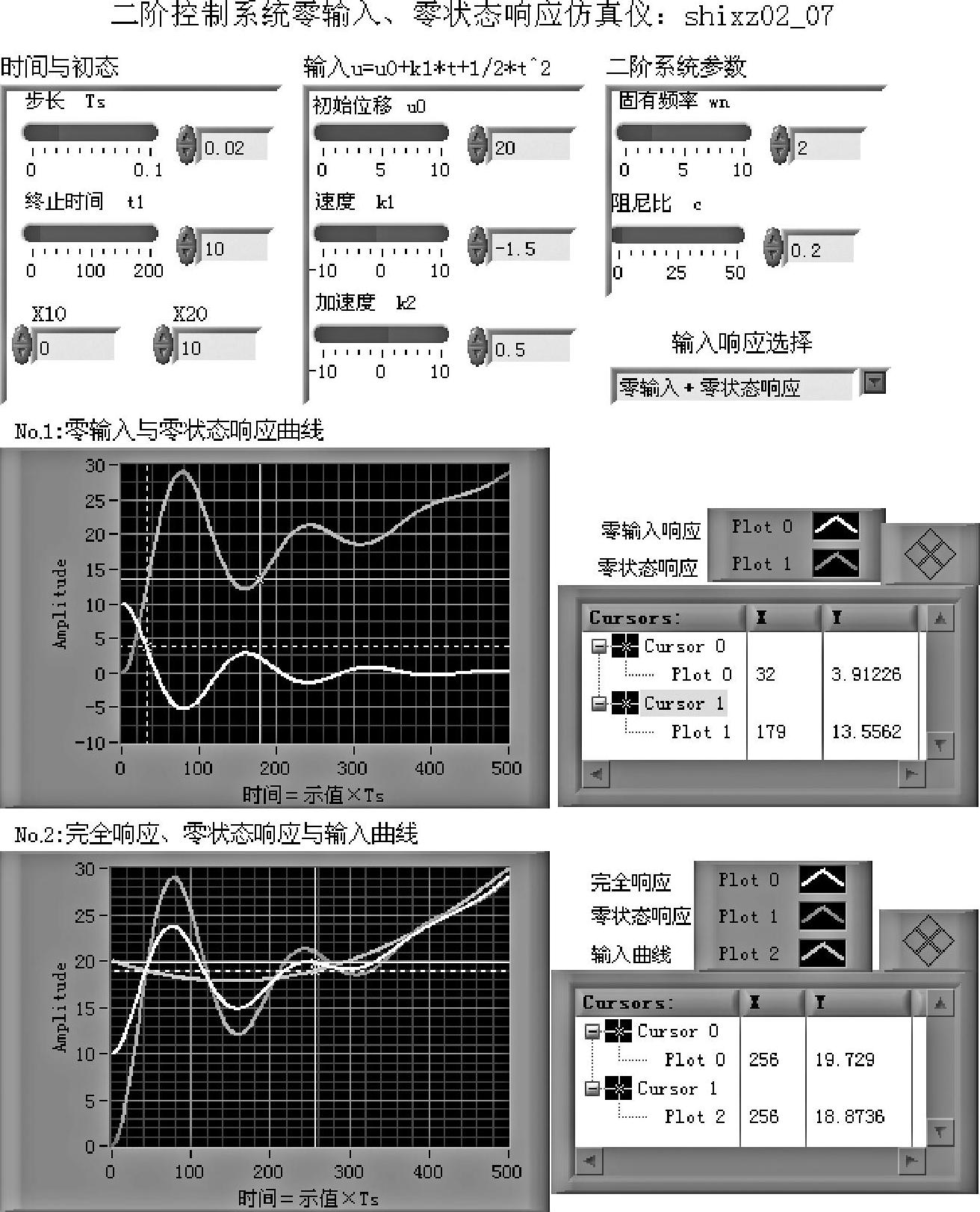
图2-3-6 程序shixz02_07前面板

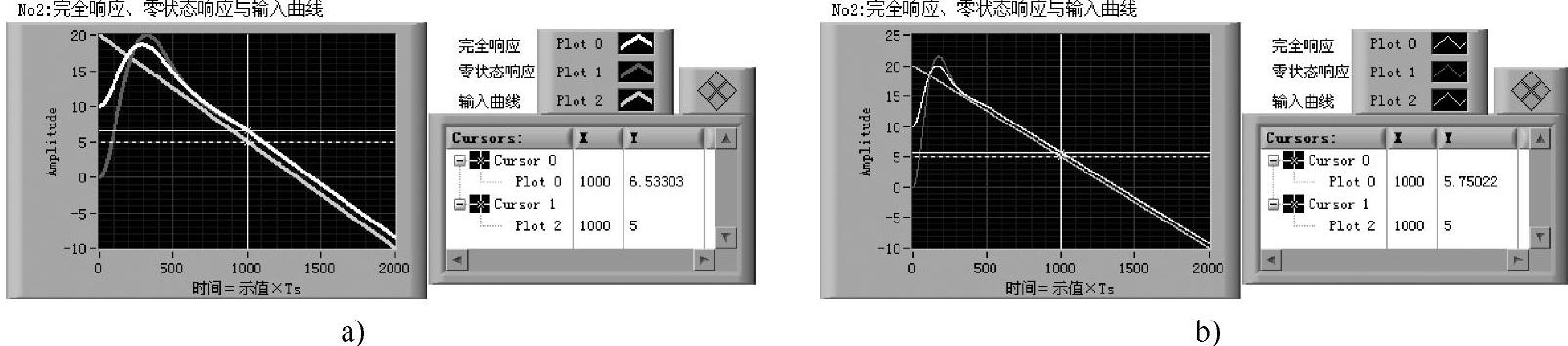
图2-3-7 二阶系统固有频率和阻尼比对恒速响应稳态误差的影响

a）ω_n=1，ξ=0.5 b）ω_n=2，ξ=0.5

前已述及，系统的零输入响应体现单位脉冲响应的规律。对于一阶系统，可以通过选择适当的初态，由其零输入响应求取其单位脉冲响应。二阶系统的单位脉冲响应与其状态之间有确定的关系。从前面的介绍可知，系统单位脉冲响应可以通过对系统单位阶跃响应求导得到。设系统输入为单位阶跃信号u=1（t），分别写出单位阶跃输入的零输入和零状态响应的输出方程

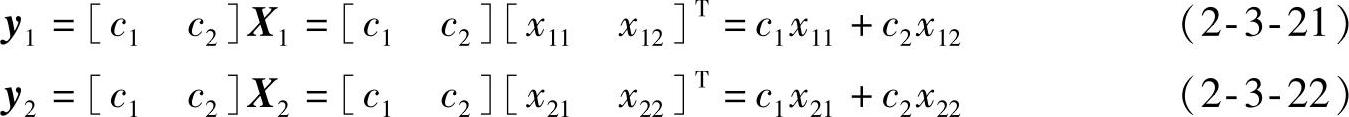
式中y₁，y₂分别表示零输入和零状态响应的输出，[x₁₁x₁₂]，[x₂₁x₂₂]分别表示零输入和零状态响应的状态变量，输出矩阵C=[c₁c₂]。

由叠加原理，系统输出的完全响应，也就是系统的单位阶跃响应输出为

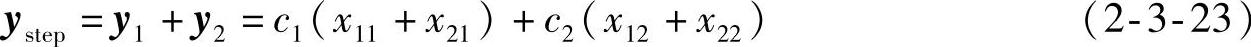
对式（2-3-23）两边求导得到系统的单位脉冲响应

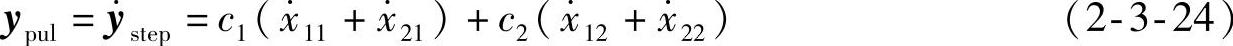
对于二阶系统，代入式（2-3-3）的输出矩阵可得c₁=0，c₂=ω²_n，状态方程x·₁₂=x₁₁，x·₂₂=x₂₁，可得单位阶跃响应和单位脉冲响应分别为

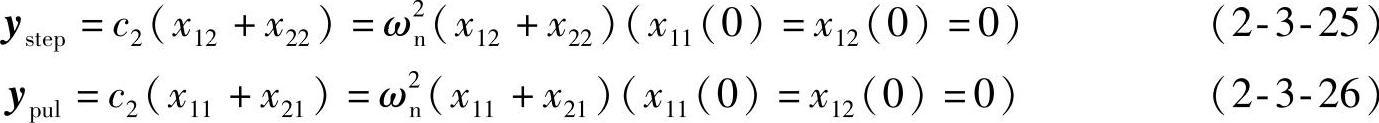
考虑到对于零输入响应，如果其初态为0，其状态轨迹也应为0，有

式（2-3-25）、式（2-3-26）与式（2-3-27）、式（2-3-28）两组式子表明，对于二阶系统，当输入为单位阶跃时，两个状态变量分别决定系统的单位阶跃响应和单位脉冲响应。阶跃响应可由输出方程表示为系统的输出，但单位脉冲响应却不反映在系统的输出上，只反映在系统输出的导函数上。由状态方程，输出的导函数由系统的另一状态决定。这个结论可以推广，例如输入为单位恒速，系统的输出为恒速响应，输出的导函数为系统的单位阶跃响应，它们分别由系统的两个状态变量决定。这表明，系统状态变量既决定其输出，也决定其输出的导函数，反映了系统的全部信息，而输出只反映系统的部分信息。

式（2-3-25）～式（2-3-28）还说明，单位脉冲响应也具有零状态响应的特征。也就是说，单位脉冲响应是一种特殊的响应，它既具有零输入响应最终会衰减为零的特征，也具有零状态响应的特征，而且，通过脉冲信号的作用，将使系统的初态发生改变。

程序shixz02_07 a给出了二阶系统状态变量曲线，其前面板如图2-3-8所示。示波器面板No.1上有3条曲线，plot0和plot1表示零输入响应的状态变量x₁₁，x₁₂。plot3表示用impulse命令绘制的系统脉冲响应曲线。No.2上也有3条曲线，plot0和plot1分别表示阶跃输入的零状态响应状态变量x₂₁，x₂₂，它们分别决定系统的单位脉冲响应和单位阶跃响应。plot2是按式（2-3-28）求出的单位脉冲响应，它是将plot0的纵坐标乘以C（1，2）=ω²_n得到的。对比表明两示波器面板上的曲线plot2是完全相同的。编程时请注意，如果阶跃响应幅值不等于1，如图2-3-8所示，在使用式（2-3-28）求单位脉冲响应时要除以阶跃幅值。该条指令应写成x21 c=C（1，2）*x21/u0。如果使用式（2-3-26）仿真单位脉冲响应（x21 c=C（1，2）*（x11+x21）/u0），应注意图2-3-8中的初态应当选择为0。

图2-3-8 程序shixz02_07a前面板

类似地，图2-3-9是程序shixz02_07 b的前面板，给出了恒速输入时状态变量轨迹、恒速响应及其导函数（单位）阶跃响应的仿真曲线。注意对比两个示波器屏幕上“单位阶跃响应”和“等效单位阶跃响应”曲线。求等效单位阶跃响应时，注意除以恒速系数k₁。通过这两个仿真实例，可以比较深刻地体会状态与输出的关系，理解“输出通常只反映系统的部分信息，状态反映了系统的全部信息”这句话的含义。

图2-3-9 程序shixz02_07b前面板