二阶控制系统的时域响应分析

1.单位脉冲响应

对式（2-3-1）进行拉普拉斯逆变换有

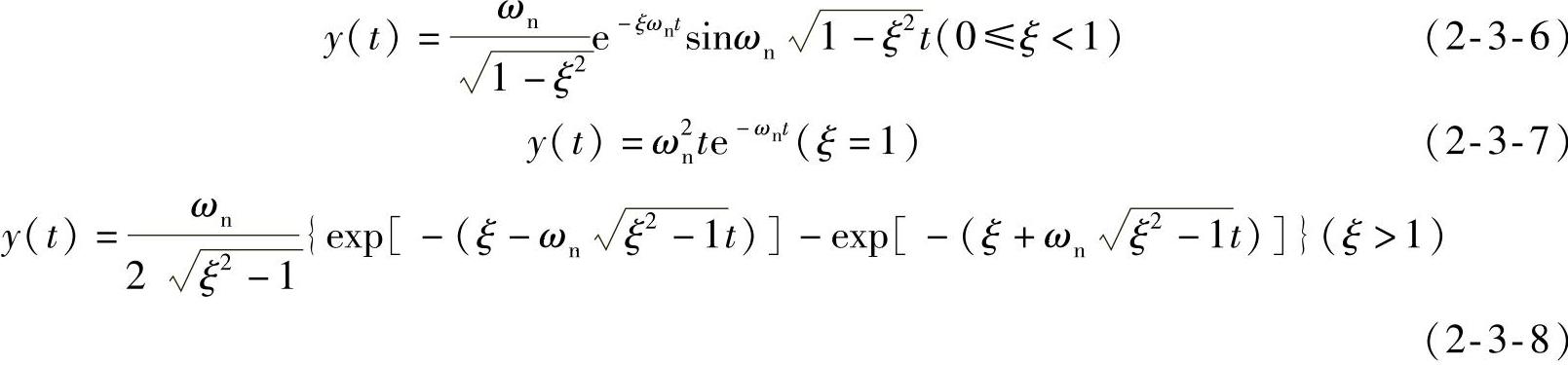
对式（2-3-4）进行拉普拉斯逆变换有

可求出二阶系统单位脉冲响应的几个特殊值。

初值：y（0）=0，可由初值定理得到。由于二阶系统含有储能器件，虽然初值为零，在冲击作用下，仍然会有持续一定时间的暂态响应。而对于无阻尼系统，由于没有能量耗散，响应呈等幅振荡。

峰值时间：对于式（2-3-6），。

响应峰值：y_m1=ω_nexp（-ξω_nt_p1）。

对于式（2-3-8），峰值时间。

响应峰值：。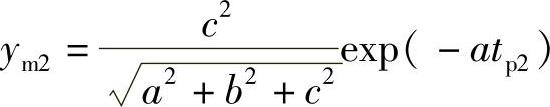

终值：y（∞）=0。除无阻尼系统外的脉冲响应终值均为0。

2.单位阶跃响应

将式（2-3-1）乘以1/s后再进行拉普拉斯逆变换有

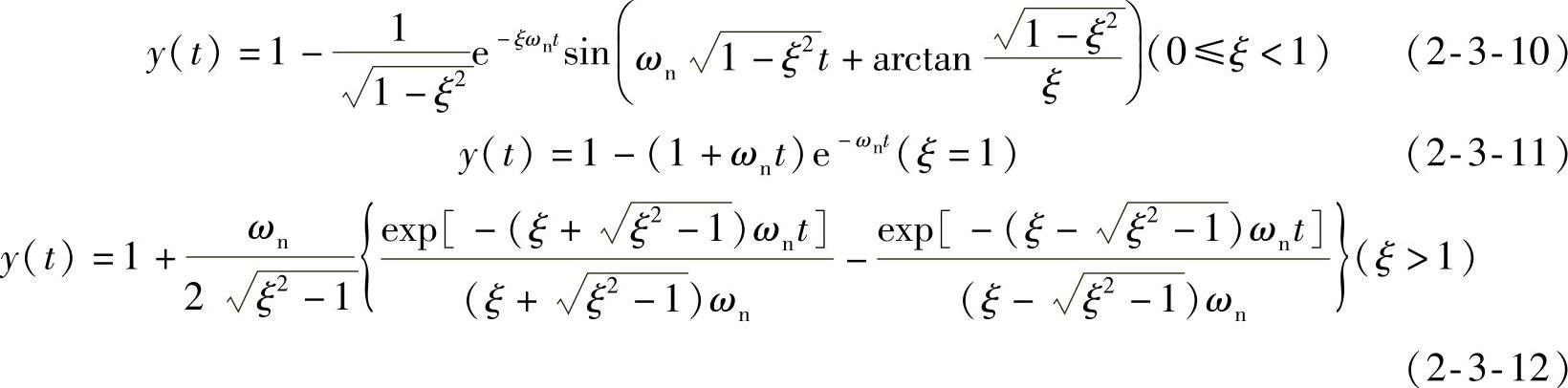
将式（2-3-4）乘以1/s后再进行拉普拉斯逆变换有

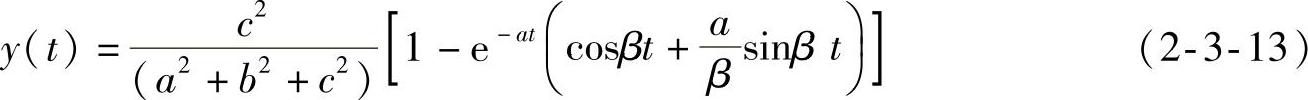
式中，。

初值：y（0）=0。

终值：对于系统式（2-3-1）的单位阶跃响应，除无阻尼系统外，y（∞）=1。对于系统式（2-3-4）的单位阶跃响应，即式（2-3-13），y（∞）=c²/（a²+b²+c²）。

稳态误差：对于式（2-3-1），除无阻尼系统外，稳态误差为0。实际上图2-3-1a中的开环传递函数是Ⅰ型系统，对于单位阶跃输入而言构成无差系统。对于图2-3-1b，其开环传递函数是零型系统，对于单位阶跃输入而言构成有差系统。e_s=1-c²/（a²+b²+c²）。

峰值时间：对于欠阻尼系统式（2-3-10），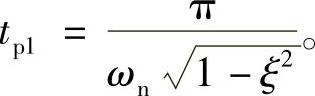

对于式（2-3-13），。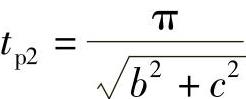

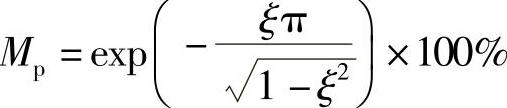最大超调量M_p；由最大超调量定义，对于欠阻尼系统式（2-3-10）有，最大超调量仅与阻尼比ξ有关。对于式（2-3-13），。(www.xing528.com)

调整时间t_ss：y（t_ss）≤（1±Δ）·y（∞），当t≥t_ss之后，输出值不越出稳态值附近的误差带Δ之外。对于欠阻尼系统式（2-3-10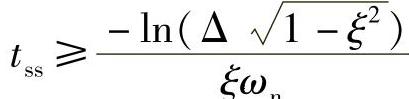），。对于式（2-3-13），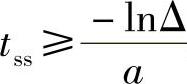

n。通常，取Δ=0.02～0.05。

3.单位恒速响应

将式（2-3-1）乘以1/s²后再进行拉普拉斯逆变换有

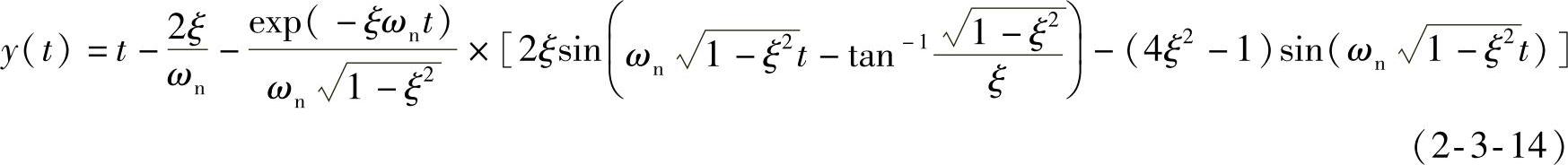
仿真表明，除ξ=1之外，式（2-3-14）均适用。当ξ=1时，式（2-3-1）的单位恒速响应为

初值：y（0）=0。

稳态误差：e_v（∞）=2ξ/ω_n。

将式（2-3-4）乘以1/s²后再进行拉普拉斯逆变换有

式中，A=a²+b²+c²，。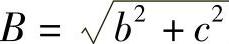

当t足够大时，误差为

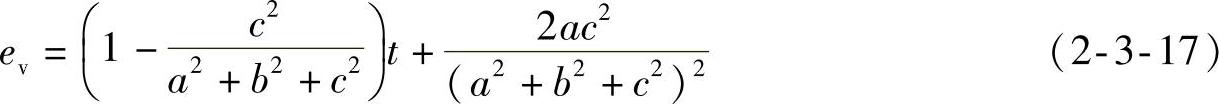
当c＞＞a+b时，。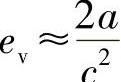

4.单位恒加速响应

对式（2-3-14）积分，根据0初始条件确定积分常数后有

式中，ω_d=ω_n。式（2-3-18）要求ξ≠1。对于ξ=1的二阶系统，其单位恒加速响应可以通过对式（2-3-15）积分得到

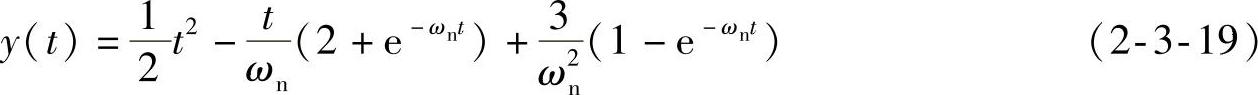
同理，对式（2-3-16）积分，可以得到式（2-3-4）的恒加速响应

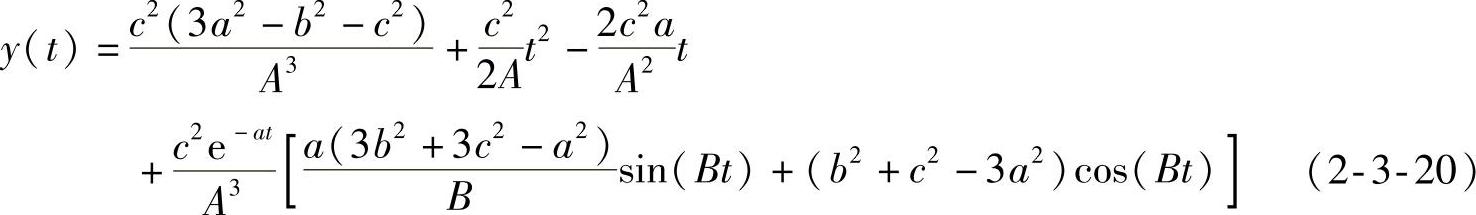
式中，A=a²+b²+c²，。