二阶控制系统的传递函数优化

二阶控制系统传递函数的标准型如图2-3-1a所示，其开环传递函数为I型系统。闭环传递函数见式（2-3-1）。

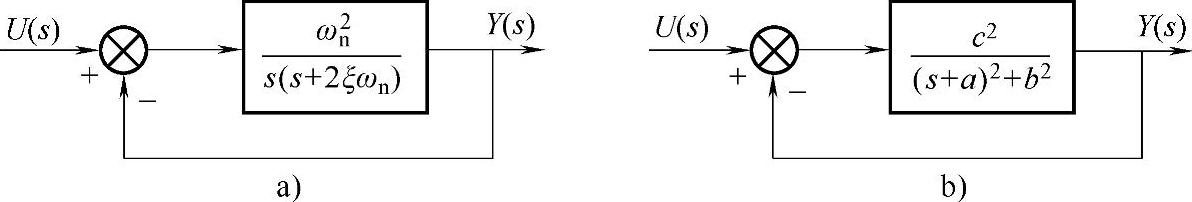
图2-3-1 二阶系统的传递函数框图

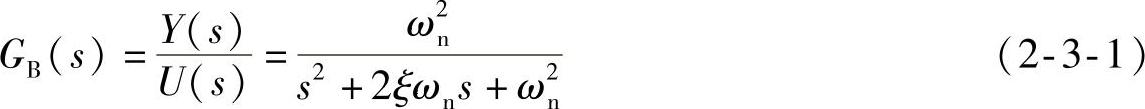
二阶系统的特征量为阻尼比ξ和固有频率ω_n。阻尼比ξ的大小决定闭环特征根的性质。当0＜ξ＜1时，闭环特征根为一对共轭复根，构成欠阻尼系统；ξ=1时为两相等的负实根，构成临界阻尼系统；当ξ＞1时为两不等负实根，构成过阻尼系统；ξ=0时为一对共轭纯虚根，构成无阻尼系统。

式（2-3-1）零极点增益模型为Z=[]（无有限零点），增益K=ω_n²。极点与阻尼比ξ密切相关。欠阻尼时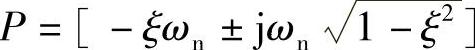；临界阻尼时P=[-ω_n；-ω_n]；过阻尼时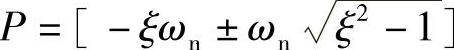；无阻尼时P=[±jω_n]。式（2-3-1）的状态方程模型如下

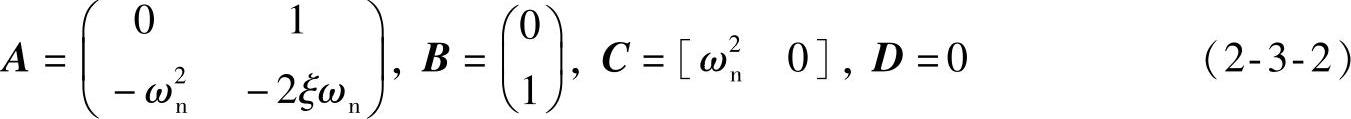
在MATLAB中，使用tf2ss命令变换得到的状态方程模型的格式为

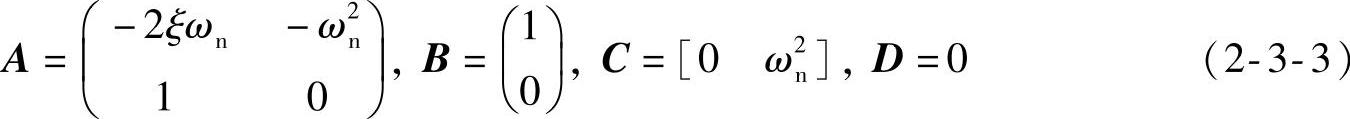(www.xing528.com)

式（2-3-2）和式（2-3-3）的区别仅在于两个状态变量互换了顺序。

式（2-3-1）的优点是特征量阻尼比ξ和固有频率ω_n的物理意义明确，性能指标可由特征量进行调节。缺点是时域响应的原函数形式较为复杂。

图2-3-1b的开环传递函数为0型系统，其闭环传递函数为

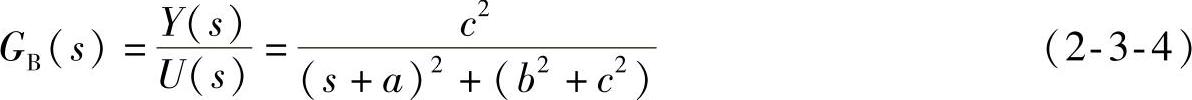
式（2-3-4）的零极点增益模型为Z=[]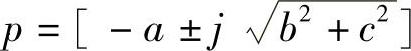，，K=c²。状态空间模型为

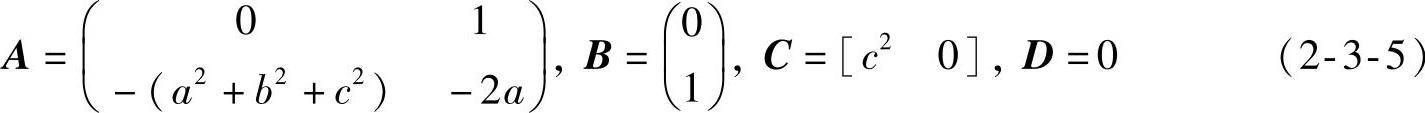
式（2-3-1）和式（2-3-4）相比，除开环传递函数型次不同，导致稳态误差性能有较大的区别之外，前者可以表示各类阻尼系统，后者通常只用来表示具有复共轭极点的欠阻尼系统。