一阶控制系统时域响应的仿真实例

【例2-4】一阶控制系统典型输入响应仿真分析仪。

一阶控制系统典型输入响应仿真程序如shixz02_04所示，程序框图面板和前面板分别如图2-2-2和图2-2-3所示。

图2-2-2 程序shixz02_04框图面板

1.赋值

在前面板的左边设有“时间设定”和“一阶系统参数”两个赋值框。时间设定框包括“步长T_s”及“终止时间t₁”两项。步长T_s既是仿真的采样周期，也是仿真曲线横坐标的最小分度。终止时间t₁设置仿真运行的最后时间。通过不同的时间设定值可以调节曲线的精细显示程度。

“一阶系统参数”包括式（2-2-2）所示的一般一阶系统的3个参数，即分子常数项k、分母一次项系数T和分母常数项l。前已述及，系统的时间常数为T/l，系统增益为k/T。

“输入响应选择”菜单式选择开关控制程序框图中的选择结构，可以任意选择一阶系统对单位脉冲、单位阶跃、单位恒速和单位恒加速激励的响应进行仿真。响应曲线和输入曲线由“输入及响应曲线”示波器面板显示。其中，曲线plot0为响应曲线，曲线plot1为输入曲线。误差曲线表示输入与响应之差，由误差曲线示波器面板显示。示波器面板上建立了随曲线移动的测量坐标系，测量值显示在示波器右侧的测量框内。示波器面板横坐标所指示的数值实际上是仿真（或采样）的点数，对应的时间值等于横坐标示数乘以步长T_s.。

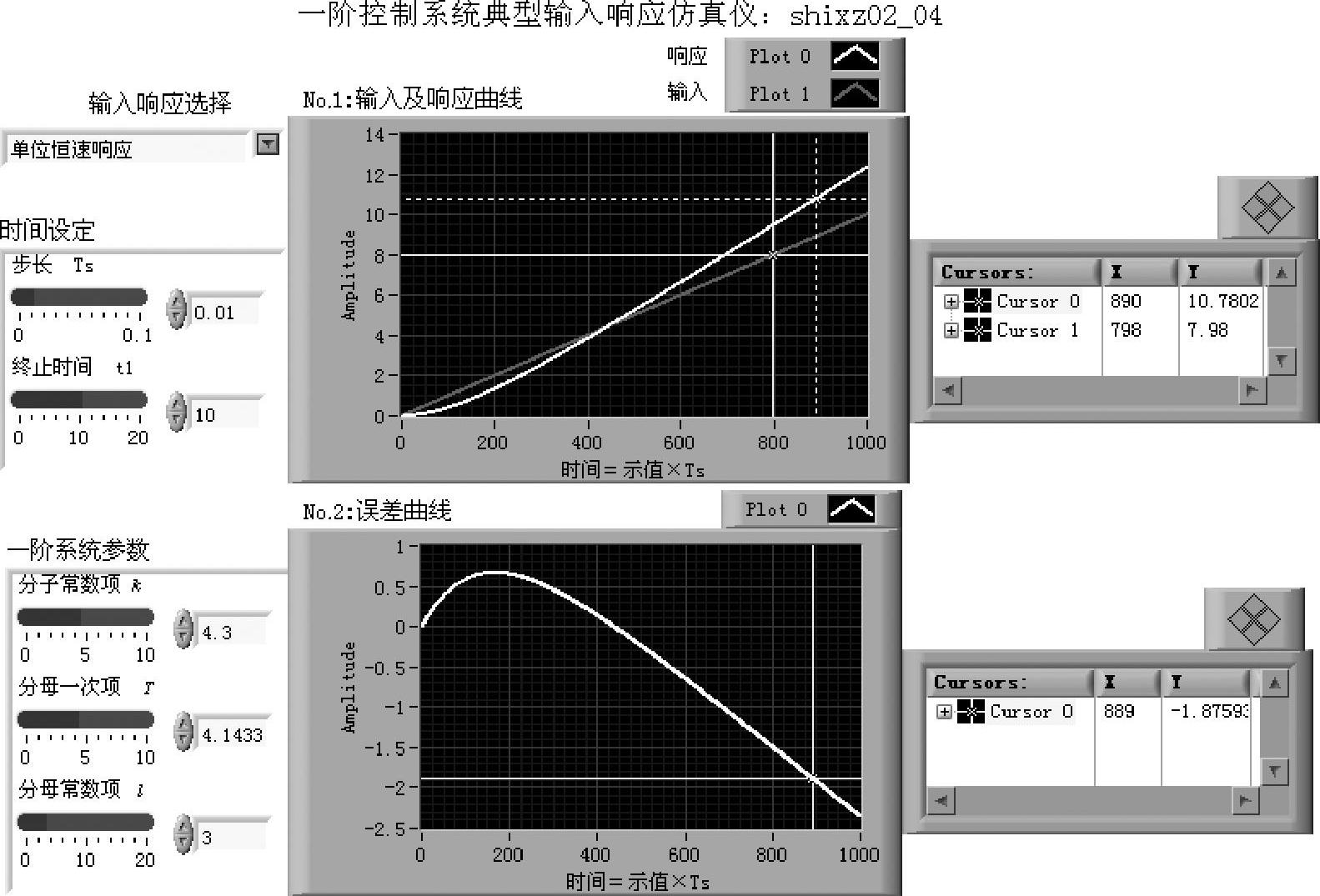
图2-2-3 程序shixz02_04前面板

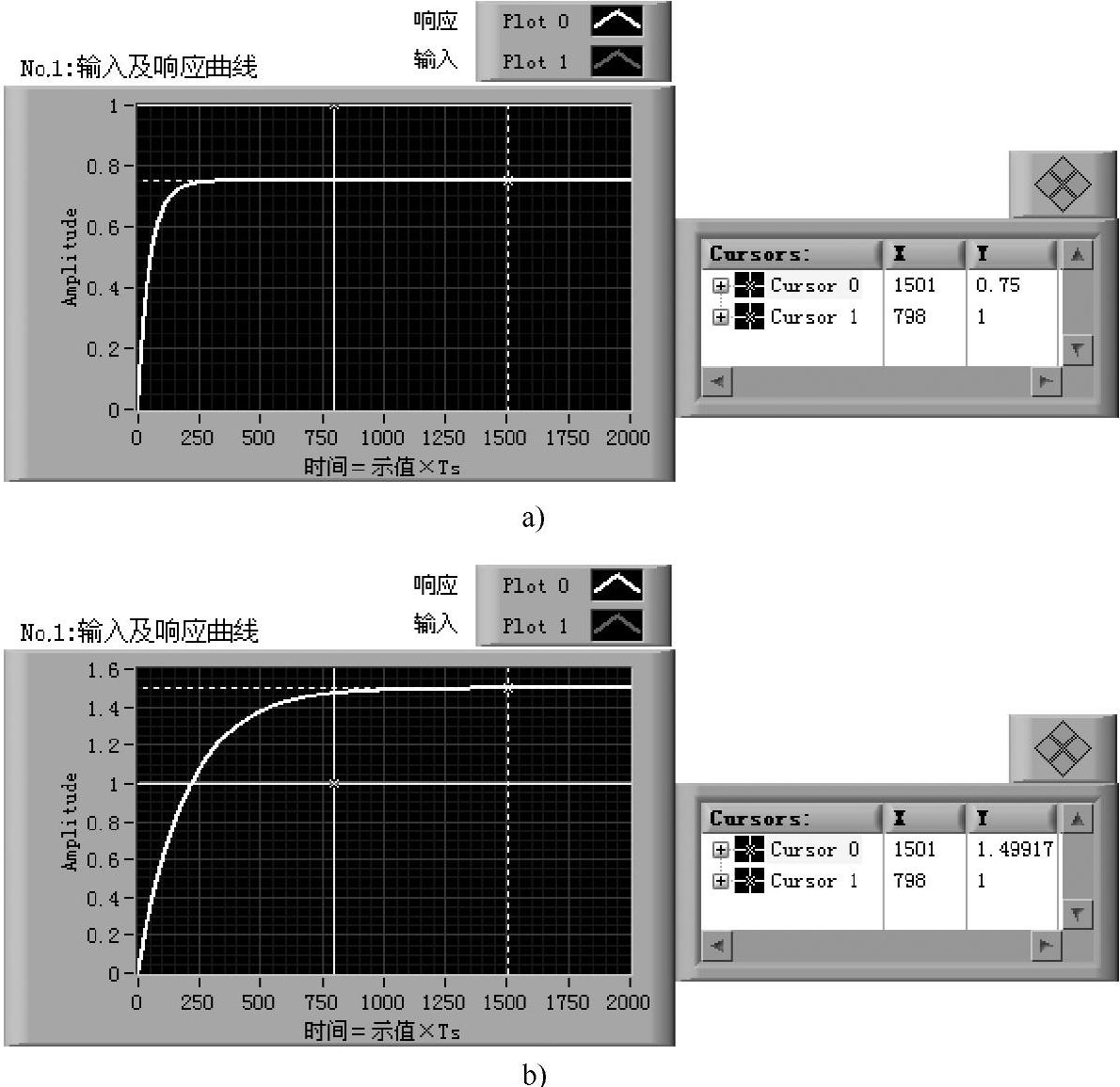
图2-2-4 系统参数对单位阶跃响应的影响

a）T/l=0.5，k/l=0.75 b）T/l=2，k/l=1.5

2.运行程序

选择一种输入响应，例如单位阶跃响应，连续运行程序，改变系统参数，可见响应曲线和误差曲线随参数改变而连续改变。例如，研究系统有效时间常数T/l对响应曲线的影响。固定k不变，当T/l的值减小时（T减小或l增大），曲线上升加快；反之，当T/l的值增大时（T增大或l减小），曲线上升变缓，如图2-2-4所示。响应曲线上升快慢与k无关。

系统参数对单位阶跃响应终值的影响。由式（2-2-6）可知，单位阶跃响应的稳态值为k/l，二者的比值越大，响应的稳态值越大，反之稳态值越小。仍以图2-2-4为例，其中图2-2-4a的k/l=0.75；图2-2-4b的k/l=1.5，二者终态值相比变化2倍，终态值与T无关。由于稳态值仅与k，l的比值有关，当k=l时，其稳态值为1，此时，系统单位阶跃响应的稳态误差为0，因为这时系统的开环传递函数为I型系统k/（T_s），系统稳态位置误差为0。

在一阶系统的3个参数中，分母常数项l的数值既影响单位阶跃响应曲线上升的快慢，也影响系统的稳态值。也就是说，分母常数项l对一阶系统的快速性和准确性均有影响。当k=l=1时，还原成标准一阶系统式（2-2-1）。

一阶系统的单位恒速响应如图2-2-5所示，其中图2-2-5a中k≠l，图2-2-5b中k=l。

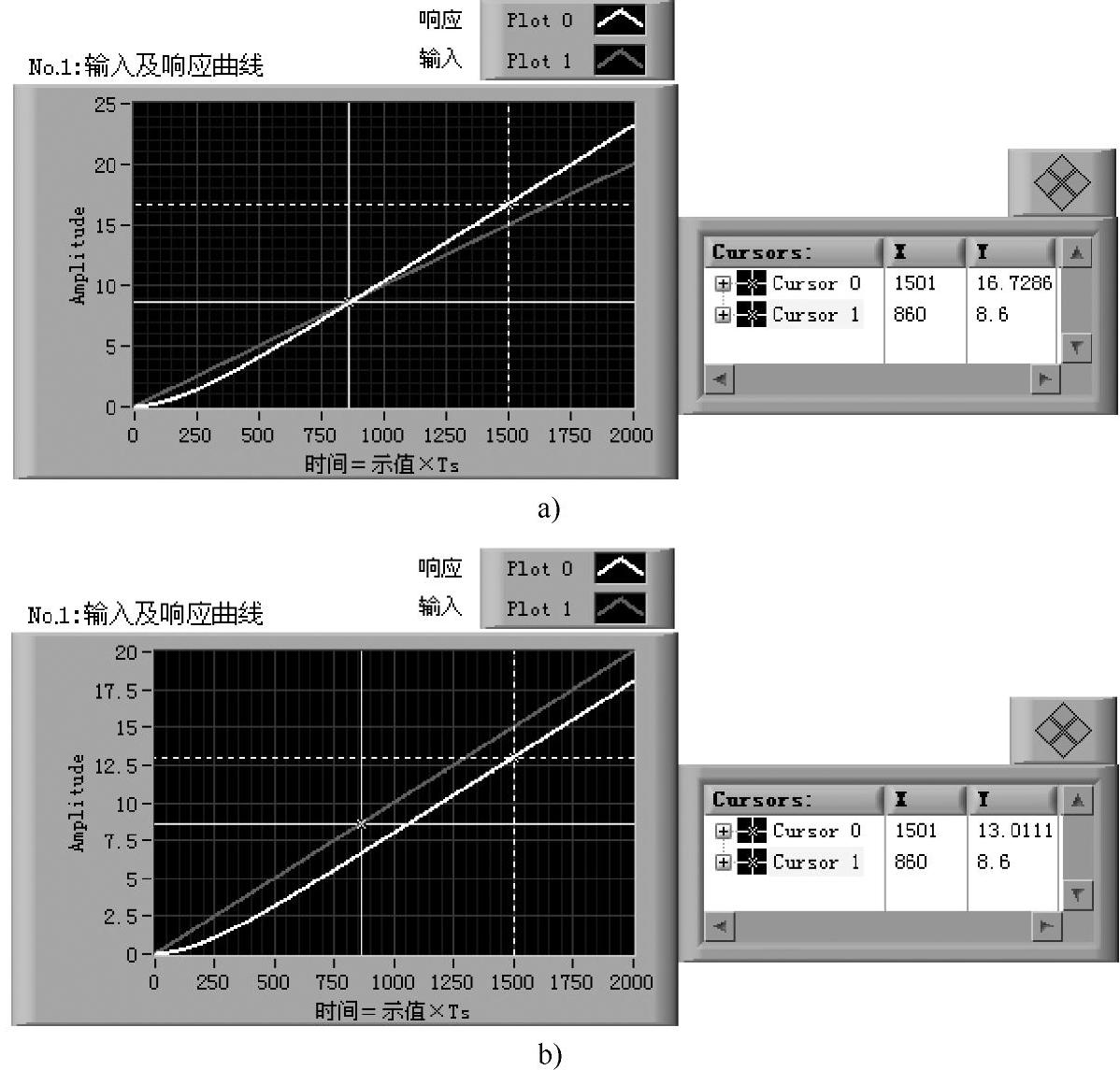
图2-2-5 一阶系统的单位恒速响应

a）k=4.5，l=3.5，T=7 b）k=l=3.5，T=7

在图2-2-5a中，由于k＞l，在t较小（本例为t＜8.9s）时，e_v（t）＞0；当t=8.9s时，输入与响应相等，e_v（t）=0；在t较大（本例为t＞8.9s）时，e_v（t）＜0，系统没有确定的稳态误差，因为系统的开环传递函数是零型系统，稳态速度误差趋于无穷。当k=l时，响应与输入曲线如图2-2-5b所示，稳态误差为T/l=2。

通过仿真可以研究，当t足够大时，恒速与恒加速响应的误差可以用式（2-2-10）和式（2-2-12）描述。如果选择k=l=1，可以仿真标准一阶系统式（2-2-1）的各种典型响应。这时，系统的单位阶跃响应是无差系统，单位恒速响应的稳态误差等于时间常数T。单位恒加速响应的误差随时间增大而不断增大。

程序shixz02_04a给出了使用lsim等命令构成的一阶系统典型输入响应仿真仪，以供参考。

【例2-5】一阶控制系统的零输入、零状态响应仿真分析仪。

上例实际上都是系统初始状态为0的零状态响应。本例将以“组合”典型信号为例，讨论一阶系统的零输入、零状态响应以及系统的完全响应。

“组合”典型信号为一匀加速运动规律的输入信号，见式（2-2-14）。通过系数的设置可以获得上例的各种典型信号。

阶跃信号：速度k₁=0，加速度k₂=0。阶跃幅值u=u₀，若u₀=1，表单位阶跃信号。

恒速信号：加速度k₂=0，u=u₀+k₁t，初始位移为u₀的匀速信号。若u₀=0，k₁=1，表示单位恒速信号。

恒加速信号：k₂≠0。选择u₀，k₁取否零值，式（2-2-14）可以构成初始位移为u₀，初速为k₁；或初始位移为u₀，初速为0；或初始位移为0，初速为k₁，以及初始位移和初速均为0的均加速信号。这些信号在工程中均有实际运用。(www.xing528.com)

在“组合”典型信号作用下一阶系统的零输入、零状态响应的仿真分析仪程序如shixz02_05所示，程序框图面板和前面板分别如图2-2-6和图2-2-7所示。

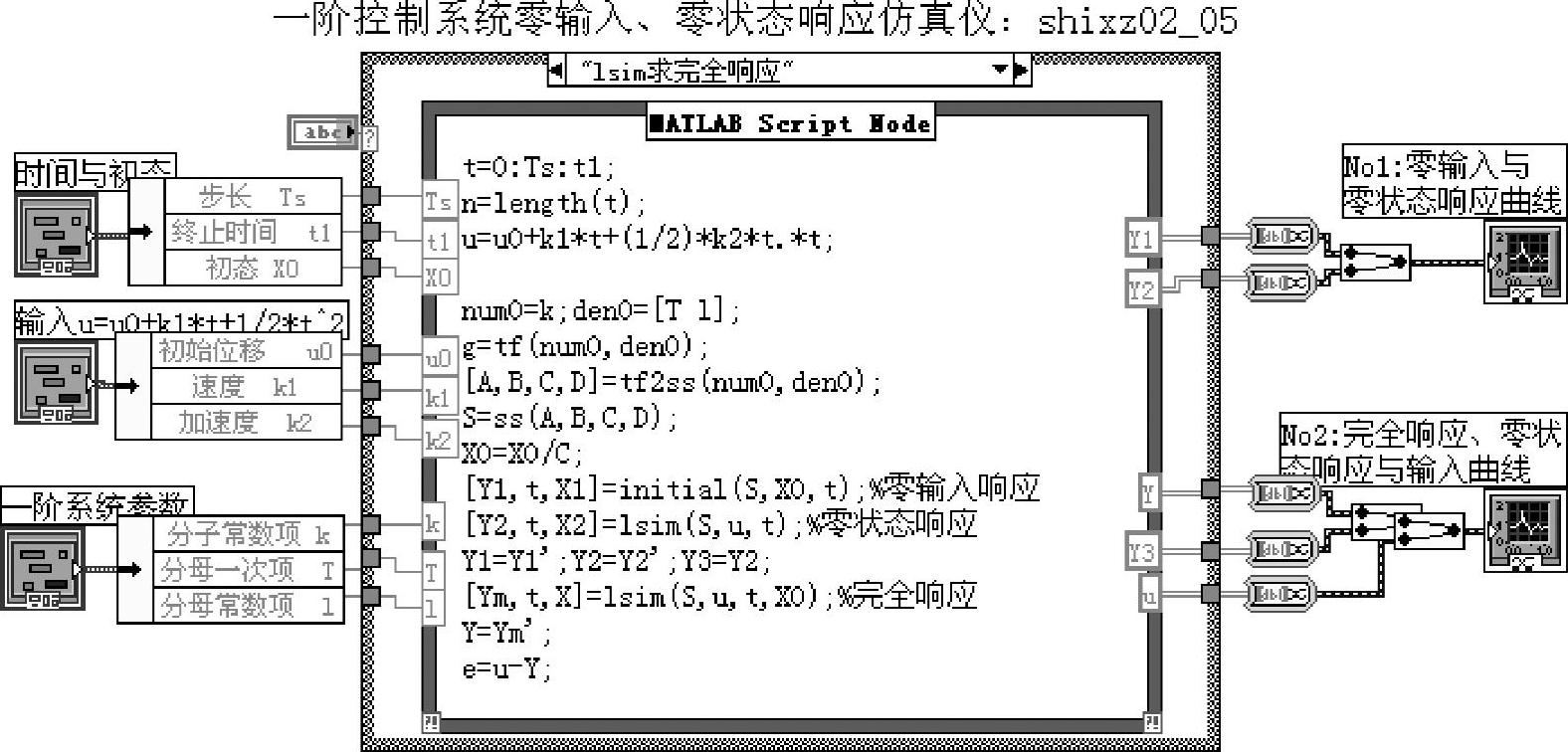
图2-2-6 程序shixz02_05框图面板

1.赋值

“输入”赋值。如前所述，通过输入信号的赋值可以选择输入信号的形式。图2-2-7中输入信号为u=40-0.3t，是一个具有一定初值的恒速信号。这种信号可以表示某一待测量，例如某容器内介质的温度变化规律。介质初始温度为40℃，降温速度为0.3℃/s，也可以用来描述热处理炉温的升温和降温规律。

初态X₀赋值。这里的初态是指一阶系统在t=0的初始值，实际上是它的输出值，而非状态值。例如，对于一个一阶温度计而言，表示的是该温度计在进行测量时已有的指示值，其余各项赋值前例已有说明。

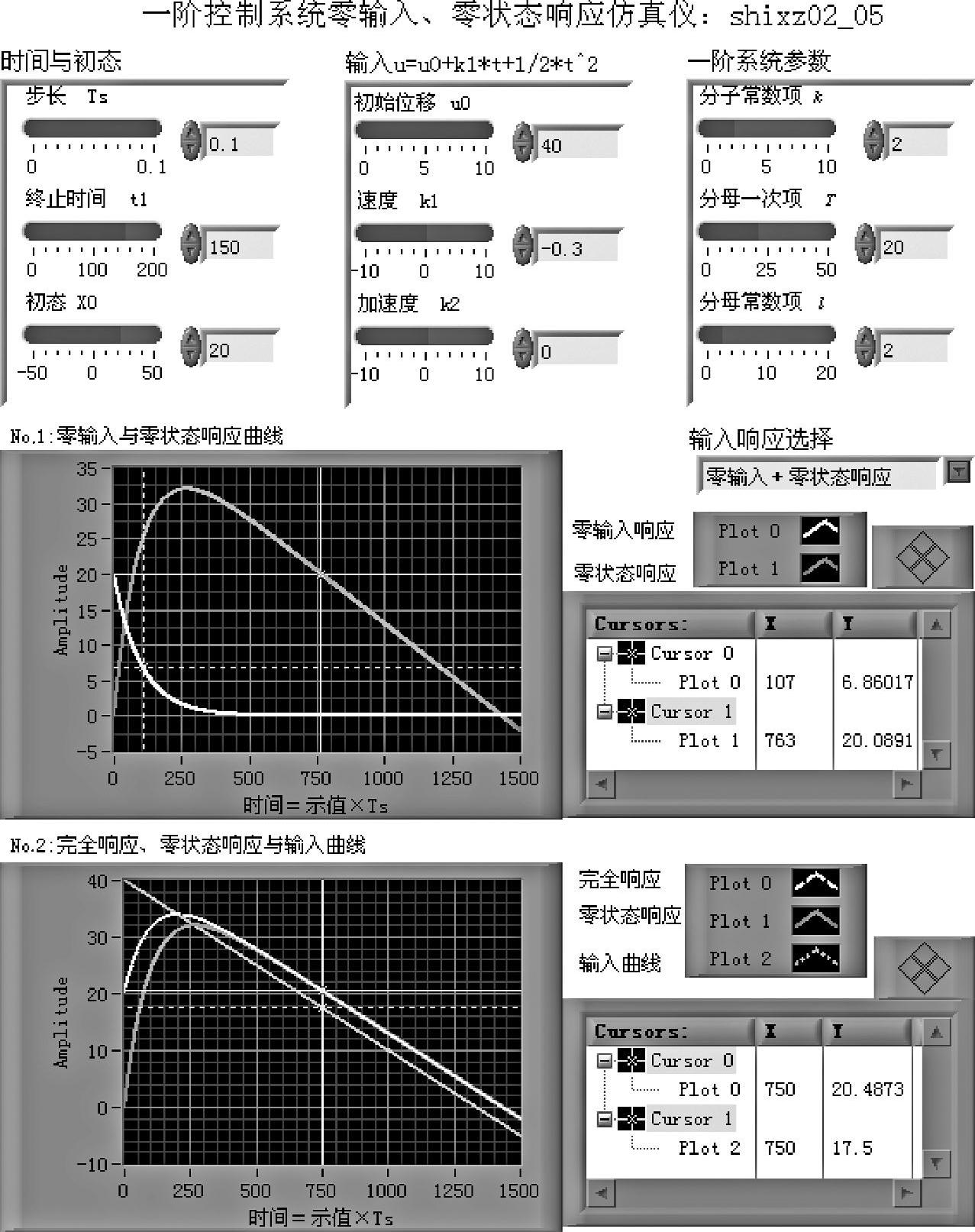
图2-2-7 程序shixz02_05前面板

2.程序特点

由于零输入响应命令

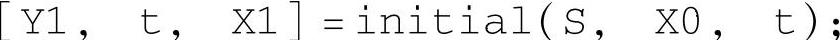
只适于状态空间模型，所以即使对于简单的一阶系统，也必须首先使用tf2ss命令将传递函数变换成状态空间模型。这里需要的是系统在某一非零初态下，不加输入时的输出响应，即需要的是返回值中的输出Y₁。输出Y₁和状态X₁满足输出方程Y1=C*X1。初态X₀所产生的初始输出也满足输出方程。在程序中实际参与运行的初态X0=X0/C，这样初始输出等于对X₀所赋的初值。

系统的零状态响应使用命令

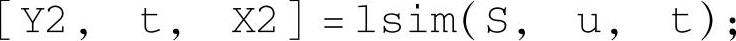
得到。有了系统的零状态响应Y₂和零输入响应，可以方便地获得系统的完全响应。在选择结构“零输入+零状态响应”中，使用零输入响应与零状态响应叠加Y₁+Y₂获得；在选择结构“lsim求完全响应”中，使用命令

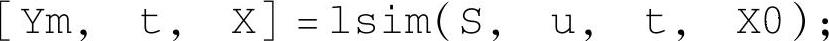
获得。仿真表明，二者结果是一致的（Y_m=Y₁+Y₂）。

3.程序运行

赋值后，选择输入响应（默认零输入+零状态响应），单击单次运行或连续运行按钮，前面板呈现两个示波器图面。No.1面板上显示2条曲线。plot0显示初态为设定值20的零输入响应曲线，plot1显示初态为零，设定输入u=40-0.3t的响应。二者之和（叠加）可得系统设定输入，在设定初态下的完全响应曲线。

示波器面板No.2上显示3条曲线。plot0为系统对设定输入，在设定初态下的完全响应曲线。plot1显示初态为零，设定输入u=40-0.3t的响应。plot2显示输入曲线。

由图可见，系统零输入响应是暂态响应，其终值为0，具有单位脉冲响应的规律（见图2-2-7上部示波器的plot0）。系统对输入的响应由输入规律决定，无论其初始状态如何，最终都跟踪输入变化，是强迫响应。在所选参数（k=l=2，T=20，k₁=-0.3）之下，系统输出响应的稳态误差为常数k₁T/l=-3（见图2-2-6下部示波器的曲线及测量值）。

如果例中的一阶系统表示某温度计的传递特性，输入是某容器内介质的温度变化规律，则零状态响应表示将示数为0℃的温度计插入容器内时，温度计示数的变化规律；完全响应则表示将示数为任意值（本例为20℃）的同一温度计插入介质时其示数的变化规律。零状态响应与完全响应这两条曲线最终重合，表明测量稳定值与刚插入介质时温度计的初始示值无关，仅由介质温度的变化规律决定。对所述的温度计而言，被测量介质的温度变化是加在温度计上的激励，温度计的测量值（示数）是对这一激励的响应。因为无论零状态响应还是完全响应接受的都是同一激励，所以两种响应的稳态值相同。

一阶系统的有效时间常数对被测量变化跟踪快慢与稳态误差的影响如图2-2-8所示，其中图2-2-8a的有效时间常数为图2-2-8b有效时间常数的10倍，图2-2-8b的测量点已测得稳态误差为-1.5，而对于图2-2-8a的同一时间测量点，输出响应还未稳定跟踪输入，还不能测量其稳态误差，虽然可以计算出稳态误差相差10倍，为-15。

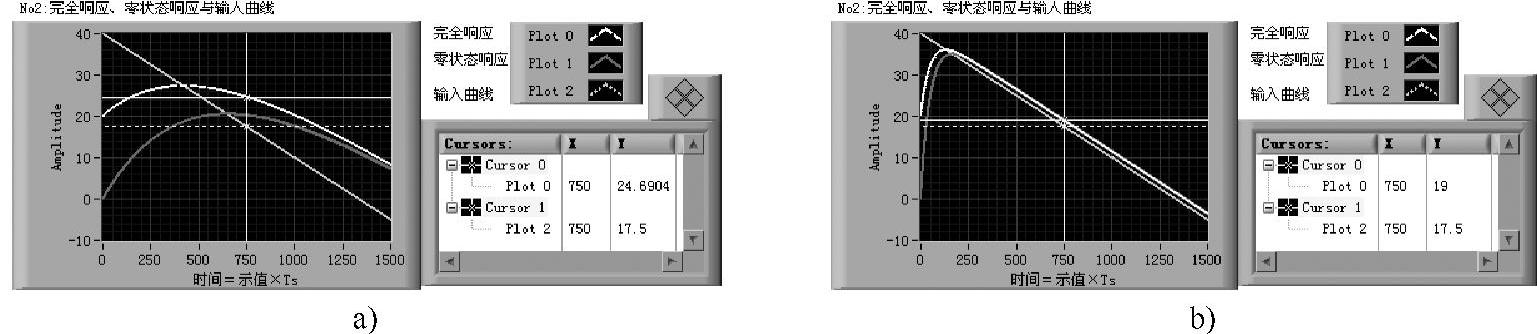
图2-2-8 有效时间常数对跟踪快慢与稳态误差的影响

a）k=0.2，T=10，l=0.2 b）k=2，T=10，l=2

如何表示单位脉冲响应的仿真曲线呢？前已述及，系统的零输入响应具有单位脉冲响应的规律，或者说，单位脉冲响应实质上是对输入为零的响应，只是初态需要重新设置。由式（2-2-4），单位脉冲响应的初值y（0）=k/T，所以要仿真系统的单位脉冲响应只需将初态X₀设置为k/T即可。用零输入响应代替单位脉冲响应如图2-2-9所示。

图2-2-9 用零输入响应代替单位脉冲响应

图2-2-9中一阶系统参数为k=4，T=2，l=3，初态X₀=2。plot0是初态X₀=k/T=2的零输入响应，也就是该一阶系统的单位脉冲响应。plot1是该系统对幅值为u₀=1.5的阶跃响应，其终值为u₀k/l=2。