1.单位脉冲响应
对式(2-2-1)进行拉普拉斯逆变换有

对(2-2-2)式进行拉普拉斯逆变换有

对比式(2-2-3)和式(2-2-4)可得单位脉冲响应的几个特殊值。
初值:y(0)=k/T,与T成反比,与k成正比。当T一定,k增大,系统增益变大,y(0)上升,反之亦反。
时间常数:T/l,与l成反比,将随着l的增大而减小。当l=1时,时间常数为T。
终值:y(∞)=0。实际上,可由终值定理y(∞)=lsi→m0s·G(s)判定,一切平衡态为0的实际物理系统的脉冲响应终值均为0。
2.单位阶跃响应
将式(2-2-1)和式(2-2-2)乘以1/s后再进行拉普拉斯逆变换
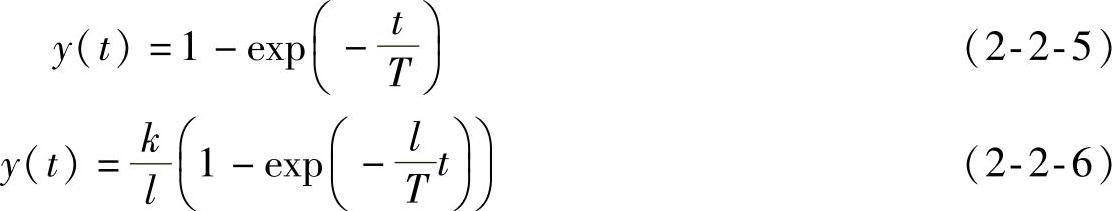
可求出一阶系统单位阶跃响应的特殊值。
初值:y(0)=0。
终值:y(∞)=k/l。当k=l时,y(∞)=1。
稳态误差:es(∞)=1-k/l。当k=l时,稳态误差为0。实际上k=l表示图2-2-1b中的l1=0,其开环传递函数是积分环节,对于单位阶跃输入而言构成无差系统。而k≠l(l1≠0),对应其开环传递函数是惯性(零型)系统,对于单位阶跃输入而言构成有差系统。
时间常数T/l由系统结构和参数决定,与输入信号无关。
3.单位恒速响应
将式(2-2-2)乘以1/s2后再进行拉普拉斯逆变换
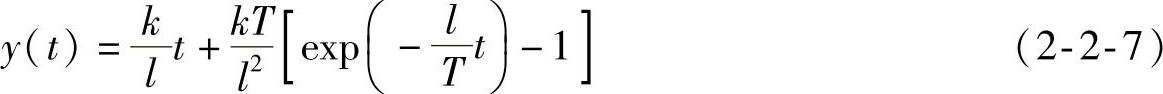
可求得一阶系统单位恒速响应的特殊值。(https://www.xing528.com)
初值:y(0)=0。
误差函数: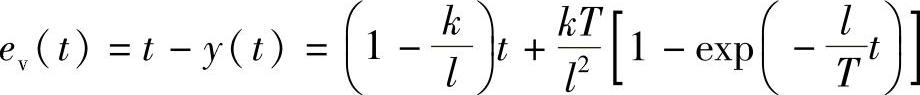 ,随t的增加而变化。当t足够大,使得指数函数exp(-lt/T)→0时有
,随t的增加而变化。当t足够大,使得指数函数exp(-lt/T)→0时有

式(2-2-8)是时间的线性函数,误差的符号由足够大项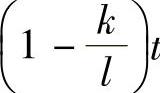 的系数符号决定。当k>l时,ev(t)<0;当k<l时,ev(t)>0。
的系数符号决定。当k>l时,ev(t)<0;当k<l时,ev(t)>0。
如果系统参数k=l,稳态误差ev(∞)=T/l。显然,对于通常所讨论的标准一阶系统式(2-2-1),k=l=1,ev(∞)=T。
如果对一阶系统式(2-2-2)输入具有一定初值的恒速信号u(t)=u0+k1t,则输出
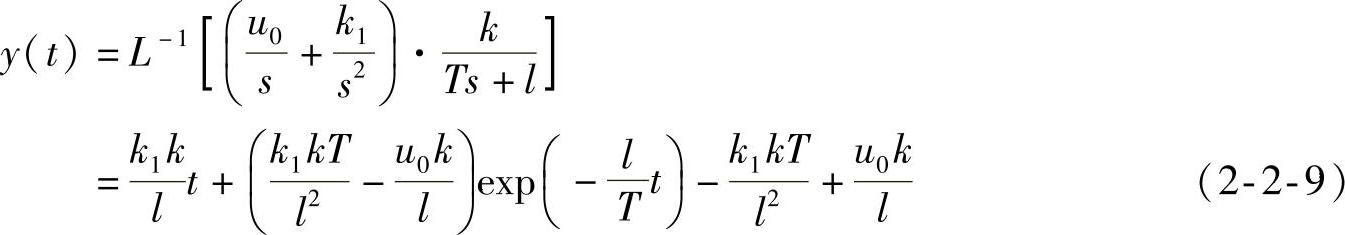
同理,当t足够大时,这种情况下的误差函数ev(t)=u(t)-y(t)为
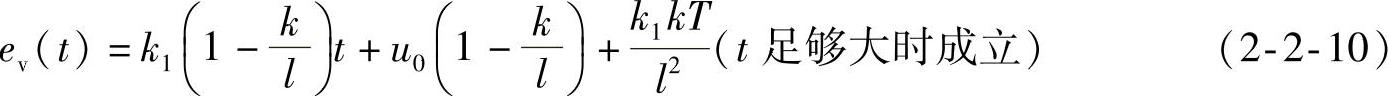
误差符号由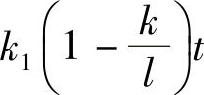 的系数符号决定,不仅与系统的结构参数有关,还与输入信号的斜率k1有关。当k=l,系统的稳态误差为(k1T/l)。
的系数符号决定,不仅与系统的结构参数有关,还与输入信号的斜率k1有关。当k=l,系统的稳态误差为(k1T/l)。
4.单位恒加速响应
将式(2-2-2)乘以1/s3后再进行拉普拉斯逆变换有
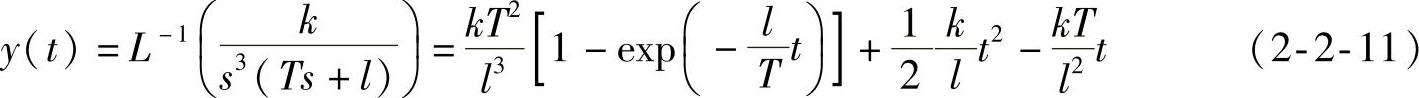
可求出一阶系统单位恒加速响应的特殊值。
初值:y(0)=0。
误差函数: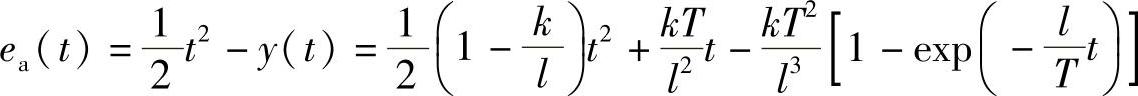 ,随t的增加而变化。当t足够大,使得指数函数exp(-lt/T)→0时
,随t的增加而变化。当t足够大,使得指数函数exp(-lt/T)→0时
是时间的二次函数。当k>l时,ea(t)是开口向下的抛物线,输入最终将小于输出;当k<l时,ea(t)是开口向上的抛物线,输入将大于输出;当k=l时,式(2-2-12)退化成时间的线性函数。在k≠l且t足够大时,误差符号由二次项的系数决定。
令式(2-2-12)等于零,可以解出误差改变符号的时间为
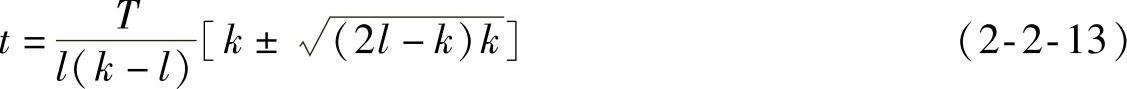
式(2-2-12)在k≠l且k<2l时有实数解。注意,上述讨论均在t足够大的条件下进行。对于t足够大的条件,如果要求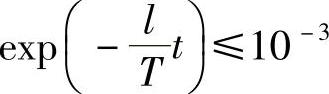 ,可选取
,可选取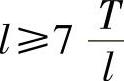 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




