MATLAB常用命令：时域响应

在MATLAB中，求取系统的时域响应有多种途径。可以直接利用专用命令step和impulse获取系统的单位阶跃响应和单位脉冲响应；可以使用lsim获取系统对任意输入的响应；对于状态空间模型，还可以使用initial获取系统在设定初始状态下的零输入响应。

1.step和impulse命令

单位阶跃响应step和单位脉冲响应impulse是典型信号输入响应仿真的基本命令，二者调用格式相同。下面以step命令为例介绍其调用格式。

sys为一个LTI（线性时不变）模型，可以是由tf生成的传递函数多项式系数模型，也可以是由zpk生成的传递函数零极点增益模型和由ss生成的状态空间模型。该命令直接绘制模型的单位阶跃响应曲线，时间范围和仿真步长由命令自动选择。对于p输出m输入的状态空间模型，将在同一幅图面上划分成p×m个子图，构成p行m列的子图布局。每个子图绘制一条输出响应曲线，分别对应系统传递函数矩阵中各传递函数的单位阶跃响应，排列顺序与传递函数矩阵相同。

该命令用于用户自己规定仿真的终止时间t₁秒，自动选择仿真步长，其余与step（sys）命令相同。

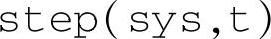
该命令用于用户自己规定仿真的时间向量t=t₀∶T_s∶t₁，其中t₀表示起始时间；T_s表示仿真步长，在离散系统中也表示采样周期；t₁表示仿真的终止时间。例如t=0∶0.01∶10，t=1∶0.1∶10等。

该命令用于在同一幅图面上绘制多个LTI模型的单位阶跃响应曲线。子图的行数等于所有系统中的最大输出数，子图的列数等于所有系统中的最大输入数。各子图上的响应曲线由各系统的传递函数矩阵决定，传递函数矩阵中某一位置的传递函数元素的响应曲线，绘制在与该传递函数位置对应的同一个子图上。如图2-1-11所示是step（sys1，sys2，sys3，t）的运行截图，包含了3个系统的单位阶跃响应曲线，sys1为三输出二输入（粗实线，处于靠上的3行和靠左的2列子图之中），sys2为四输出三输入（粗虚线，4行3列子图），sys3为二输出三输入（细实线，2行3列子图）。

上面几条命令的共同特点是直接在屏幕上绘制模型的单位阶跃输出响应曲线，而不返回任何数值数据。下面的几条命令则是返回数值数据而不作图，如果要作图，需要使用另外的作图命令。

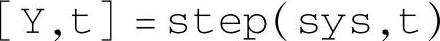
用于返回输出Y。Y的数组格式为[LT NY NU]，其中LT=length（t），决定仿真的点数，也是数组的行数。NY表示输出数p，NU表示输入数m。Y的数据格式为Y（：，：，j），其中j表示输入序号。例如，运行如下简单程序：

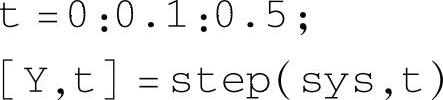
图2-1-11 step（sys1，sys2，sys3，t）的运行截图

某次运行结果如下：

Y（：，：，1）表示由输入u₁所引起的输出（全部行和列）。本例为3个输出（3列）。仿真时间0.5s，步长0.1s，6个仿真数据（6行）。Y（：，：，2）表示由输入u₂引起的输出，格式与Y（：，：，1）相同。根据线性系统的叠加原理，由两个输入u=[u₁u2]共同引起的输出为

YY表示系统的3个阶跃响应输出。

[Y，t]=step（sys，t）也可以写成[Y，t]=step（sys），这时仿真点数由系统自动决定，数据不受用户调节。如果同时需要返回阶跃输入时系统的状态轨迹值，可以使用命令

状态向量X的返回格式为[LT NX NU]，与输出向量Y类似，含义相同。因为本例模型为4阶（n=4），对应状态变量数NX为4。语句返回的X有4列，依次表示4个状态分量（x1，x2，x3，x4）的轨迹值。对于同一系统，运行该语句有

同样，也可以根据叠加原理求出在u=[u₁u₂]共同作用下的状态轨迹数值。可以验证，使用叠加原理后，系统输出、状态及输入满足输出方程Y=CX+DU，不过编程时要注意矩阵乘法的相容性。

对于SISO系统，上述命令，除涉及状态变量的语句[Y，t，X]=step（sys，t）之外，全部有效。语句中的模型sys由tf和zpk命令生成。

在命令step（sys1，sys2，...，t）中，多个模型sys1，sys2...，可以混用tf、zpk和ss命令构成的模型。当然，子图数由输入输出数最多的ss模型决定，所有用tf、zpk模型的响应曲线都绘制在第1个子图上。

impulse的调用格式和使用方法都与step命令相同，只需将上述命令中的step换成im-pulse，即可求出模型的单位脉冲响应。前已述及，在使用单位冲击信号近似单位脉冲信号时，必须保证矩形冲击的持续时间（横坐标）足够小和幅值（纵坐标）足够大。

2.单位恒速响应和单位恒加速响应的求法

单位恒速和单位恒加速响应有两种求法。第一种方法使用step或impulse命令，第二种方法使用lsim命令。先介绍第一种方法。

由于单位阶跃、单位恒速和单位恒加速信号的拉普拉斯变换顺次为1/s、1/s²和1/s³，在SISO系统中，利用拉普拉斯逆变换求这些典型信号的响应时，需要使原传递函数分别增加1个、2个和3个零极点。如果预先对传递函数添加1个零极点（即乘以1/s），再求其单位阶跃响应，实际上是在原传递函数增加2个零极点（即乘以1/s²）的情况下进行拉普拉斯逆变换，得到系统的单位恒速响应。同理，如果预先对传递函数添加2个零极点再求其单位阶跃响应，可得该系统的单位恒加速响应。所以，使用命令step求系统的单位恒速和单位恒加速响应，只需预先对原系统分别添加1个和2个零极点即可。其主要程序段如下：

当然，也可以使用单位脉冲响应命令impulse求系统的单位阶跃、单位恒速和单位恒加速响应，只需在原传递函数分别添加1个、2个和3个零极点即可，此处不再赘述。

【例2-1】求下列传递函数的单位恒速和单位恒加速响应

编制并运行上段程序，再使用plot命令作图，可得单位恒速和单位恒加速响应曲线分别如图2-1-12和图2-1-13所示。图中虚线分别表示单位恒速和单位恒加速信号。

下面介绍使用lsim命令求任意输入响应，包括求单位恒速和单位恒加速响应的方法。和step命令相比，lsim命令也有直接作图和返回参数两种方式，但其调用格式的最大特点在于必须规定输入的函数形式。调用命令

可以直接绘制模型sys在输入U作用下的响应曲线。对于SISO系统，输入U是时间的标量函数；对于MIMO系统，U构成输入向量，其列数等于输入数。例如，对于3输入状态空间模型，输入U包含3个分量，记为U（t）=[u₁（t）u₂（t）u₃（t）]。当求该系统单位恒速响应时，输入U（t）是含有3个分量的恒速信号，在程序中写成

图2-1-12 单位恒速响应曲线图(www.xing528.com)

图2-1-13 单位恒加速响应曲线

时间t的格式与step命令相同。使用语句

可以指定初始状态值X₀。当默认X₀时，命令默认初态为0。此命令仅适用于状态空间模型，对于传递函数模型，指定的非0初始状态无效，因为传递函数是在0初始条件下定义的。

【例2-2】绘制一个三阶三输出三输入状态空间模型的单位恒速响应。程序如下：

某次运行结果如图2-1-14a所示。在同一幅面上出现3幅子图，分别表示输入向量U所产生的3个输出响应。注意，这与step命令输出不同，step命令绘制每个输入分量所产生的输出阶跃响应曲线，每条响应曲线与传递函数矩阵中的各个传递函数一一对应。而lsim命令所绘制的各条响应曲线已经考虑了各输入分量的叠加效应，每条响应曲线对应传递函数矩阵中的一行。图2-1-14a中的细实线是机器自己添加的恒速输入曲线。

用于在同一幅图上作出多个系统sys1，sys2...，在输入U作用下的响应曲线。图2-1-14b示出了两个三阶三输入三输出的单位恒速响应曲线。命令中的sys1，sys2，...系统必须具有相同的状态数、相同的输入数和相同的初始状态，但各系统的输出数可以不同。读者可以思考两个输出数不同系统响应曲线的分布情况。

图2-1-14 某三阶三输入三输出的单位恒速响应曲线

用于返回模型对输入U响应的数值数据。向量Y的行数由length（t）决定，其列数等于模型的输出数，不直接作图。当使用plot（t，y）作图时，所有输出响应曲线绘制在同一个直角坐标系内，不分成子图。

用于返回模型对输入U的输出响应Y和状态轨迹X的数值数据，不作图。可以验证，返回的输出Y和状态X满足输出方程YY=C*X′+D*U′。

如果要求系统的单位恒加速响应，只需输入单位恒加速信号

即可。对于MIMO系统，输入U的列数同样应当等于系统输入数。上面为了说明单位恒速响应的求法，所举实例中输入U的各分量为相同信号，实际上，各输入分量可以是不同的函数。

最后讨论一下在求单位脉冲响应时，使用lsim与impulse命令所产生的误差。前已述及，lsim命令中必须给出输入U的函数形式，而理想单位脉冲信号的持续时间趋于0，幅值趋于无穷，不能表示成通常的时间函数。lsim命令中的单位脉冲信号只能使用幅值足够大，持续时间足够小且冲击强度为1的信号来近似。下面通过一个实例仿真看看两种响应之间的误差。

【例2-3】仿真式（2-1-7），讨论单位脉冲响应与单位冲击响应的差别。

仿真图如图2-1-15所示。图中实线是单位脉冲响应曲线，虚线是单位冲击响应曲线。其中图2-1-15a的单位冲击信号高宽比为100，单位脉冲响应与单位冲击响应范数相对误差为0.17%。图2-1-15b的单位冲击信号的高宽比为25（更改上段程序中的步长T=0.2），单位脉冲响应与单位冲击响应范数相对误差为0.66%。

图2-1-15 单位脉冲响应与单位冲击响应的比较

注意：在求取由gensig生成的单位脉冲信号的响应yu2时，幅值变换因子（T_s）的处理方式。考虑幅值变换因子后，yu₁与yu₂的效果相同，表明单位冲击信号u₁和由gensig生成的单位脉冲信号的功能相同，将u₂，yu₁，yu₂绘制在同一幅图上，如图2-1-16所示。

图2-1-16 单位脉冲与单位脉冲响应

3.状态空间模型的零输入响应仿真命令initial

状态方程式（1.3.1）的完全响应可以写成零输入响应和零状态响应之和

前已述及，可以使用命令lsim仿真系统的完全响应和零状态响应，但不能仿真系统的零输入响应。系统零输入响应的仿真命令为initial，调用格式如下：

该命令可以直接绘制系统在初始条件X₀，输入为0时的输出响应曲线。其中，初值X₀为n×1列向量。命令将在同一幅面上绘制p（输出数）幅子图，每幅子图上呈现一条曲线，对应一个输出分量的零输入响应曲线。例如对于三输入三输出系统，各子图的分布类似于图2-1-14a。显然，此命令绘制的是齐次状态方程输出Y的仿真曲线。

该命令用于按照用户设定的仿真终止时间t₁，绘制系统零输入响应曲线。对于离散系统，未规定采样周期，t₁表示采样数。注意格式中X₀与t₁的位置与lsim命令不同（下同）。

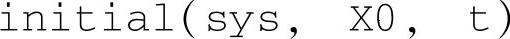
该命令用于按照用户设定的时间格式t=t₀∶T_s∶t₁，绘制系统零输入响应曲线。

该命令用于同时绘制多个系统的零输入响应仿真曲线，子图数等于各子系统的最大输出数。

不直接绘图，返回输出向量Y，状态向量X和时间向量t。其中Y和X的行数等于length（t），Y的列数等于输出数p，X的列数等于状态数n。

nitial的仿真实例见下面相关章节。