离散与连续状态空间的相互转换描述

前面已经介绍连续与离散SISO系统的相互转换，下面介绍MIMO系统中连续与离散描述方法的相互转换。

1.离散与连续系统各系数矩阵的关系

设n阶m输入p输出连续系统为

对应的离散系统为

X（kT+T）=FX（kT）+GU（kT）

Y（kT+T）=CX（kT）+DU（kT） （1-4-4）

上面两式中各系数矩阵都是相容的，离散系统的采样周期为T，t=kT。在保证Y（t）=Y（kT）的前提下，连续与离散系统中的输出矩阵C和直传矩阵D相同。状态矩阵与输入矩阵可按式（1-4-5）和式（1-4-6）计算：

2.离散与连续系统转换的主要指令

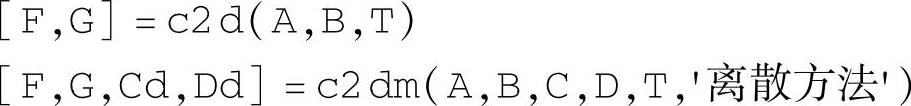
上述指令用于返回离散系统的各系数矩阵。命令C2d与c2dm的区别在于，后者可以由用户自己指定离散方法，MIMO系统的离散方法有′zoh′、′foh′、′tustin′和′prewarp′四种。c2d使用默认的零阶保持器法′zoh′。使用命令c2d离散，输出矩阵与直传矩阵对应等于连续系统的C、D。

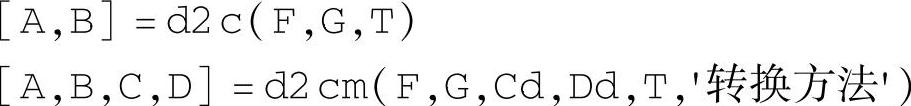
上述指令用于将离散系统连续化，返回连续系统的系数矩阵，基本上是c2d与c2dm的逆操作，只是对于MIMO系统连续化的方法只有′zoh′、′tustin′和′prewarp′三种。

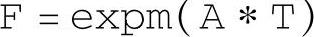
上述指令用于返回矩阵指数函数式（1-4-5）的结果，与使用′zoh′方法用c2d与c2dm命令计算出的状态矩阵F相同。(www.xing528.com)

【例1-18】状态空间连续化、离散化转换。

程序如shili01_18所示。程序框图面板和前面板分别如图1-4-4和图1-4-5所示。

程序说明：

程序使用上述4种允许的离散方法，对随机连续系统S₁和手动赋值系统S₂进行离散化。运行程序时，首先将“赋值运行”开关置于左边的“赋值”，手动输入S₂系数矩阵和采样周期数值（否则不能正常运行）。离散化结果分别显示于“S₁：离散化”和“S₂：离散化”板块之中。“矩阵指数函数”板块示出式（1-4-5）和式（1-4-6）的计算值，其中Fm1和Hm1为S₁离散化后的系统矩阵和输入矩阵，Fm2和Hm2为S₂离散化后的系统矩阵和输入矩阵。

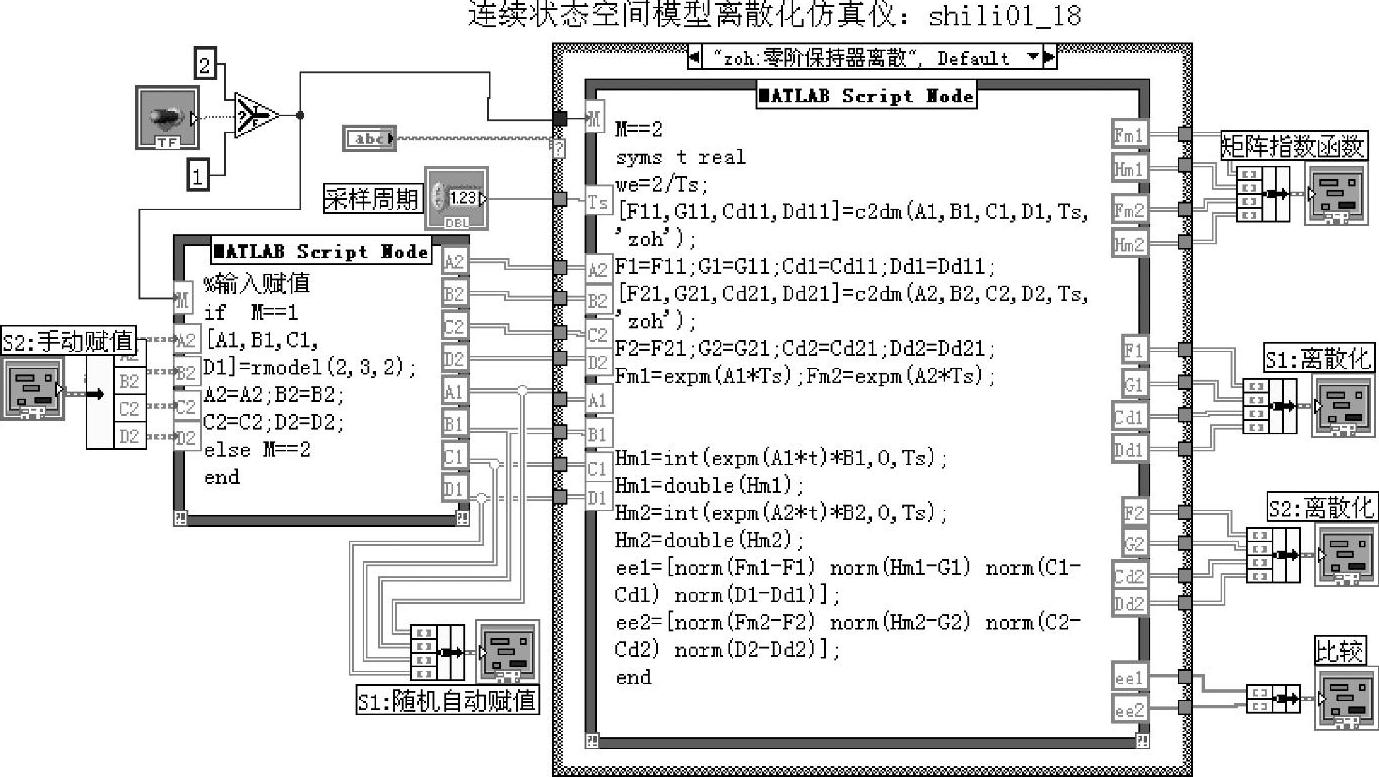
图1-4-4 程序shili01_18框图面板

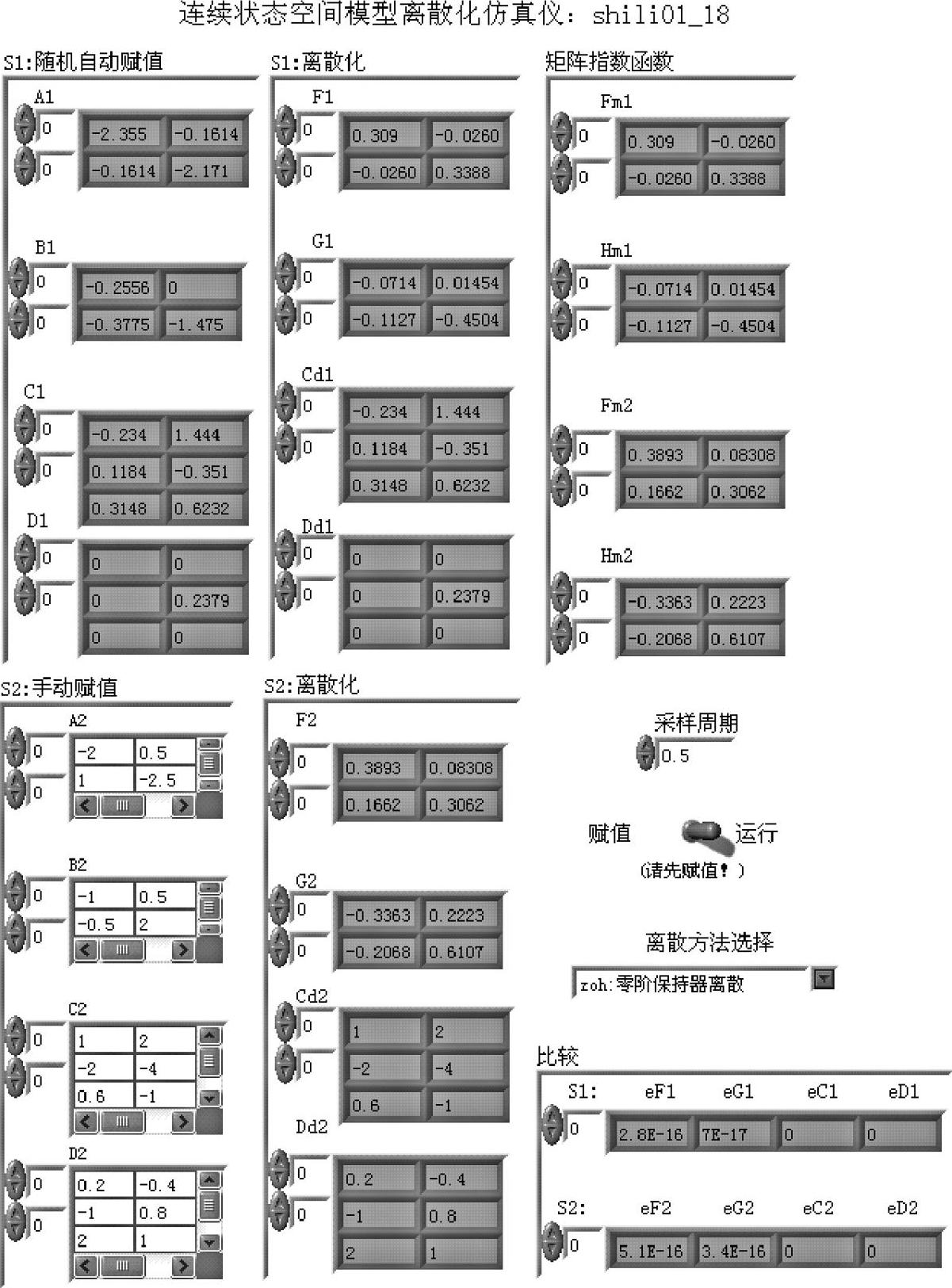
图1-4-5 程序shili01_18前面板

“比较”板块分别就S₁和S₂两个系统，使用不同离散方法所得的对应系数矩阵进行比较。其中，eF1=norm（F1-Fm1），表示式（1-4-5）与命令c2dm所得系统矩阵的比较；eG1=norm（G1-Hm1），表示式（1-4-6）与命令c2dm所得输入矩阵的比较；eC1=norm（C1-Cd1），eD1=norm（D1-Dd1）分别表示离散系统与连续的输出矩阵和直传矩阵的比较。eF2、eG2、eC2和eD2表示针对系统S₂的比较。图1-4-6给出了某次运行几种离散方法的比较结果。

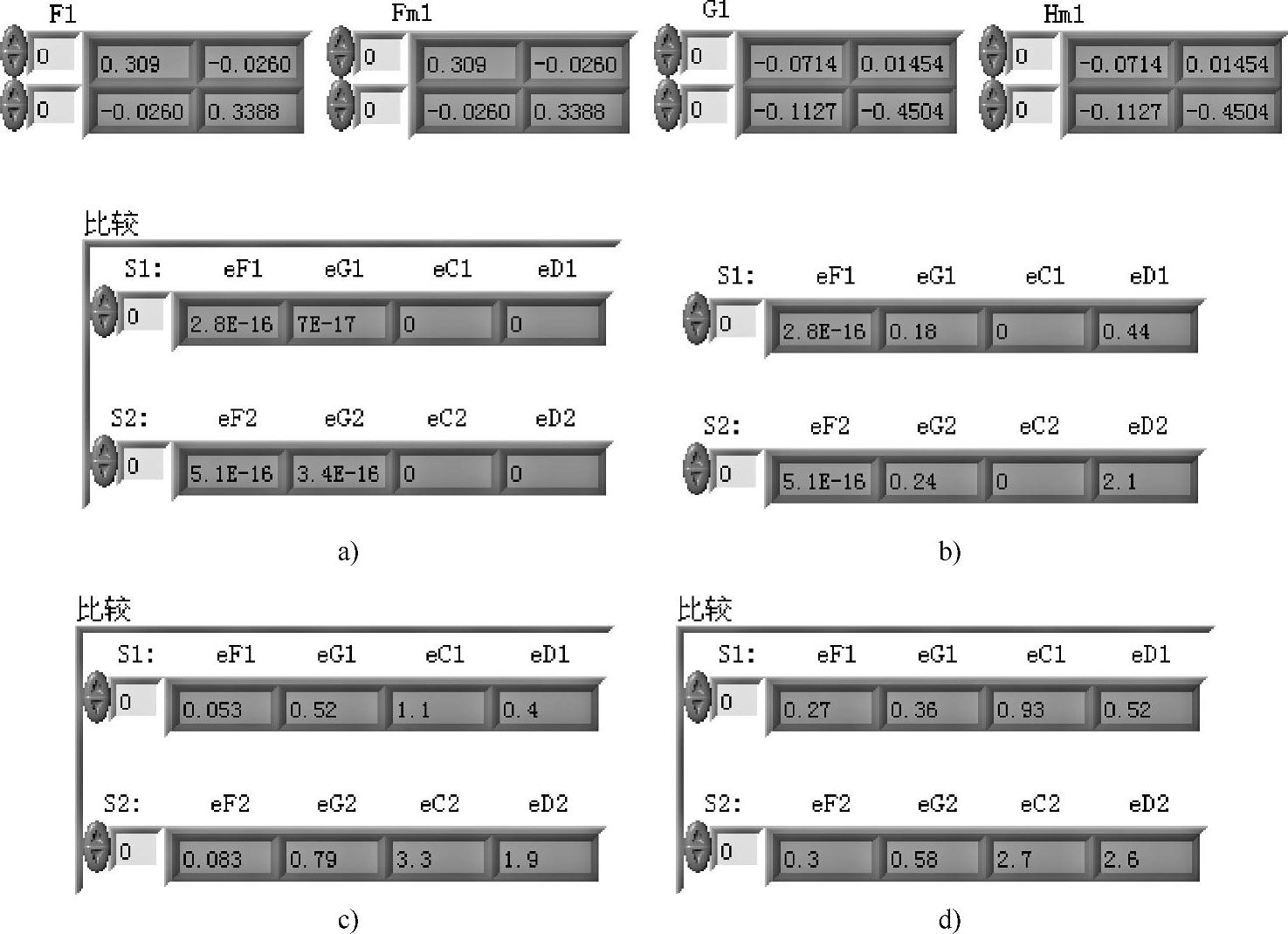
图1-4-6 不同离散方法结果比较

a）零阶保持器法离散 b）一阶保持器法离散 c）双线性变换法离散 d）预曲双线性法离散

由图1-4-6可见，式（1-4-5）对零阶和一阶保持器法成立。式（1-4-6）仅对零阶保持器法成立。实际上，式（1-4-6）正是在零阶保持器的条件下推导出来的结果。同时还看到，离散系统与连续系统的输出矩阵与直传矩阵也只是对零阶保持器法才对应相等。

读者还可以在连续运行条件下，改变采样周期，观察采样周期对离散结果的影响。

如果将程序（见图1-4-5）输入改为离散系统，主要指令改为d2cm，则可以研究离散系统的连续化。