MATLAB离散状态空间描述的主要指令

1.离散状态空间对象和系数矩阵

离散系统中的主要命令如下：

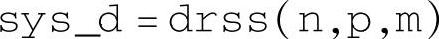
该命令用于返回n阶m输入p输出随机离散状态空间对象。

[A，B，C，D，E，T]=dssdata（sys_d）；%此处A，B分别对应式（1-4-1）的F和G

该命令用于返回各系数矩阵及采样周期等数值“描述符”。

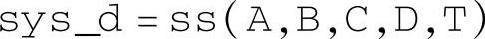
该命令用于在已知系数矩阵A、B、C、D和采样周期T的条件下，构造离散状态空间对象。

注意：drss命令不规定采样周期，返回值为随机离散对象，每次运行后对象均可以改变。对于由drss生成的对象，当使用dssdata命令求数值描述符时，返回的采样周期T=-1。ss命令规定采样周期T的具体数值，返回由（A，B，C，D）所生成的确定对象，该对象不因所指定的采样周期而改变。如果sys_d是一个连续模型，则dssdata命令返回采样周期T=0。

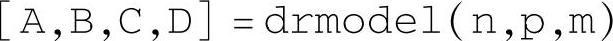
该命令用于返回稳定的离散状态空间系数矩阵，无采样周期信息。

2.转换成传递函数的多项式模型

状态空间模型转换成传递函数的多项式及零极点增益模型，可以先转换成对应的多项式及零极点增益对象，再获取多项式系数和零极点增益的具体数值。也可以反过来，先求多项式系数和零极点增益的具体数值，再求其对应的对象表达式。二者的语法有些差别，需要留意。下面的讨论假定已执行本节第1小节中获取离散状态空间模型sys_d的各条命令，即已对离散状态空间模型sys_d赋值。

转换成多项式对象的相关命令如下：

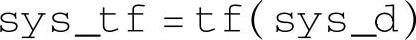
该命令用于返回p×m个传递函数多项式对象，分别列出从输入1到输入m对所有输出的传递函数表达式，每个输入的传递函数对应传递函数矩阵的一列，见式（1-3-3）。

获取多项式系数的具体数值分成两步，先获取多项式系数的单元数组，命令如下：

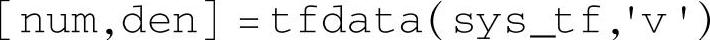
该命令返回传递函数分子、分母多项式的单元数组，只给出各个多项式系数的个数，不给出具体数值。例如，对于三阶二输入三输出对象，返回

注意：在返回的分子单元数组num中，多项式系数个数虽然相同，但并不表明各分子多项式的阶数相同，因为返回值包括分子多项式高次项的0系数在内。

由多项式单元数组获取系数值的命令如下：

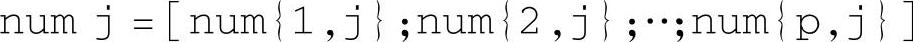
其中，j=1，2，…，m。对应每个j值，返回值有p行。分别表示输入1到输入m对所有输出的传递函数分子多项式系数值。

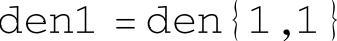
该命令用于返回所有传递函数分母多项式的系数。

注意：在从单元数组获取实际数值时使用大括号“{i，j}”格式，不使用“zij=Z（i，j）”的矩阵元素提取格式，因为单元数组各单元元素个数不一定相同，不构成矩阵。也可以使用ss2tf命令先求多项式系数值，再使用tf命令求取对应的多项式对象表达式，使用命令

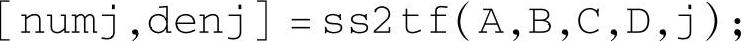
返回输入1到输入m对所有输出的传递函数分子、分母多项式数值（行矢量）。分子多项式系数numj有p行。分母多项式系数有1行，且所有传递函数的分母多项式均相同。

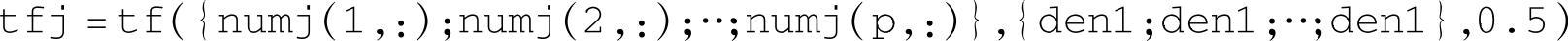
其中，j的含义同上。对应每个j值，右端第1对“{}”内包含p个分子多项式系数行矢量numj，p个分母多项式系数行矢量den1以及采样周期数值。tfj返回系统输入j对所有p个输出的传递函数的多项式表达式，对应传递函数矩阵的第j列。当然也可以按类似格式将全部p×m个分子多项式系数、分母多项式系数den1输入右边的两对“{}”内，返回传递函数矩阵的所有p×m个传递函数，不过所返回的这些传递函数是从1到乘积p×m依次编号的，不明显提供由哪个输入对哪个输出所构成的传递函数信息，也就是说这种返回值不表示某传递函数在传递函数矩阵中的位置。

3.转换成零极点增益模型(www.xing528.com)

转换成零极点增益对象的相关命令如下：

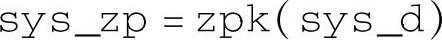
该命令用于返回传递函数的零极点增益对象，显示形式与tf命令相同。

获取零极点增益数值命令也分成两步，先获取零极点增益的单元数组，命令如下：

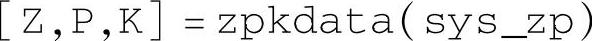
该命令用于返回传递函数零极点增益的单元数组，只给出各个传递函数零极点的个数，不给出具体数值。例如，对于三阶二输入三输出对象，某次运行返回为

注意：在所返回的零点单元数组中，输入2对输出1和输出2所构成的传递函数只有两个零点，其余的有3个零点。这说明各传递函数的零点个数不一定相同，而且对于随机赋值的状态空间模型，每次运行的情况都可能不同。原因是每次随机赋值的输入矩阵和直传矩阵对零点数的影响不同。对于极点则没有这个问题，返回的各极点单元数组中均有个数相同的极点。下面会看到，各极点的数值都相同，因为一个系统具有唯一确定的特征值。增益K则返回其具体数值，构成p×m维数值矩阵。

由单元数组获取零极点增益数值的命令如下：

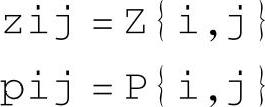
其中，i=1，2，…，p；j的含义同上。分别返回各传递函数零点值zij和极点值pij。返回值zij中不包括无穷远零点，所以各zij返回值的行数（个数）不一定相同，也就是各传递函数零点数不一定相同。各pij返回值的行数（个数）相同。实际上pij=P{i，j}可以用p11=P{1，1}代替，表明同一系统，所有传递函数都具有相同的极点。

也可以使用ss2zp命令先求零极点数值，再使用zpk命令求取传递函数的零极点增益对象表达式，所用命令如下：

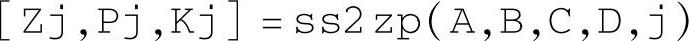
其中，j的含义同上。对应每个j值，Zj返回n×p维数值数组，对应第j输入与所有p个输出所生成的传递函数的零点，每个传递函数均有n个零点（显示为n行），包括无穷远零点“inf”在内，构成1列；Pj返回系统的n个极点；Kj返回对应第j输入的p个传递函数的增益值。

由于Zj中可能含有无穷远零点，而使用命令zpk获取传递函数的零极点增益对象时，不支持无穷远或0值的零极点，所以在使用由ss2zp所获取的零极点增益再转换成对象模型时，需要先排除Zj中的无穷远零点，然后使用生成零极点增益对象的命令（以n=3，p=3为例），所用命令如下：

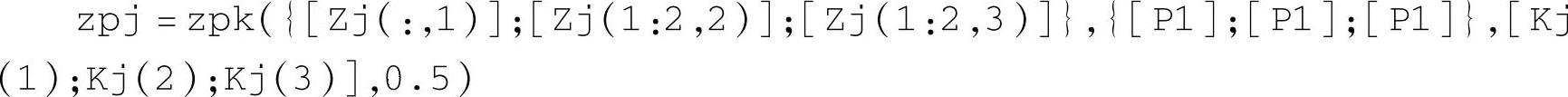
其中，j的含义同上。对应每个j值，右端第1对“{}”内依次放置输入j的各传递函数所有零点构成的一个单元数组，每个传递函数的零点构成一个列矢，不得含有无穷远零点；右端第2对“{}”内放置对应的p组极点，也构成一个单元数组；对应的p个增益构成列矢置于“[]”之内。最后指定采样周期的数值。语句返回系统输入j对所有p个输出的传递函数的零极点增益表达式，对应传递函数矩阵的第j列。要特别注意剔除了无穷远零点之后的表达方式，如[Zj（1：2，2）]表示输入j与第2输出之间的传递函数有两个有限零点，1个无穷远零点。

此外，对于将传递函数多项式系数和零极点增益转换成状态空间模型的逆向命令tf2ss和zp2ss，传递函数多项式与零极点增益模型的相互转换命令tf2zp与zp2tf，语句格式前面已讨论（参见第1章）。对于MIMO系统，以输入j为依据，每次转换一个输入比较方便。需要注意的是，由tf2ss和zp2ss所获得的状态空间模型与原始模型是等价的，具有相同的特征值。但由于状态变量选择的多样性，各系数矩阵与原始矩阵一般是不同的。

【例1-17】离散状态空间模型转换仿真仪。

将离散状态空间模型转换成传递函数和零极点增益形式。程序如shili01_17所示。程序框图和前面板图分别如图1-4-2和图1-4-3所示。

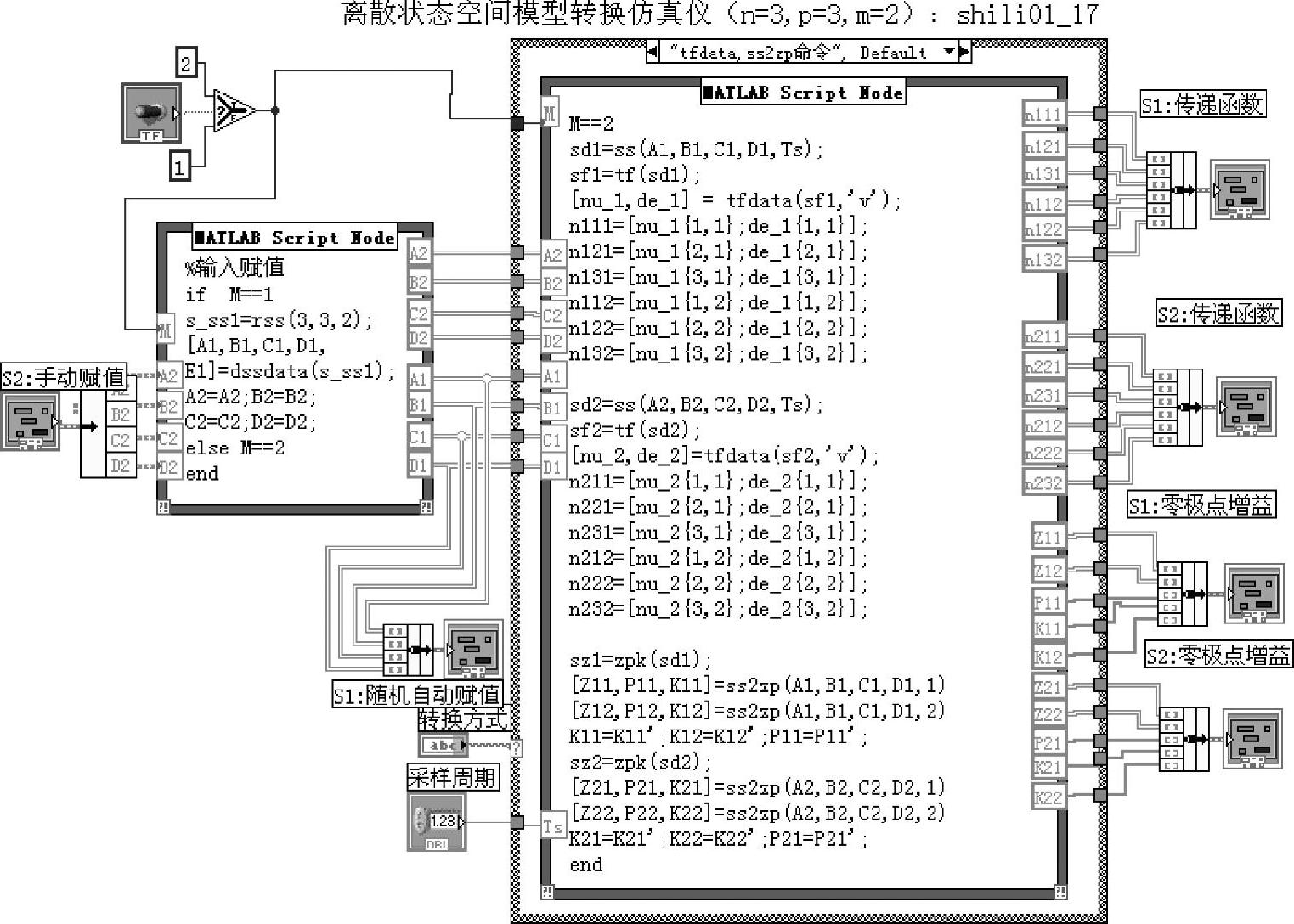
图1-4-2 程序shili01_17框图面板

程序说明：

运行程序首先赋值。为便于对比，程序设置了随机自动赋值生成的离散系统S₁，用户手动赋值生成的离散系统S₂。设置了两个选择结构，第1个选择结构程序先使用tfdata命令，获取传递函数的单元数组，再由单元数组获取传递函数的多项式模型，仿真数据如图1-4-3a所示。第2个选择结构使用ss2tf和ss2zp命令，直接由状态空间获取多项式系数和零极点增益数值，如图1-4-3b所示。

由tfdata命令获得的传递函数多项式模型，已经进行了零极点对消，得到的是传递函数的约简形式，如图1-4-3a所示；而由ss2tf命令所获得的传递函数不进行零极点对消。两种选择结构在进行零极点转换时直接使用ss2zp命令，保留全部零极点，如图1-4-3b所示。

在显示传递函数分子、分母多项式系数时，每两行构成一个二维数组，表示一个传递函数。第1行表示分子系数，第2行表示分母系数。前3个传递函数是输入1对3个输出的传递函数，后3个传递函数是输入2与输出构成的传递函数。当实施零极点对消后，同一系统的传递函数分母是不同的，因为已经消去了部分乃至于全部极点。

在零极点增益板块中，一个传递函数的零点排成3行，形成一个列矢。同一个输入与全部输出生成的传递函数零极点依次排成3列，如Z11等。系统的极点排成一个行矢，如P11等。增益也排成行矢，如K11、K12等，分别表示两个输入所生成的传递函数的增益。

注意：增益为0和含有无穷远零点时对应传递函数的特点。

图1-4-3 程序shili01_17前面板