典型连接在1.3.4连续系统状态空间模型中的应用

连续系统状态空间模型的典型连接也有串联、并联和反馈等几种。由于状态空间模型常常用来描述MIMO系统，它们的连接比起SISO系统的连接要复杂一些。

设两个状态空间模型子系统S₁、S₂分别为

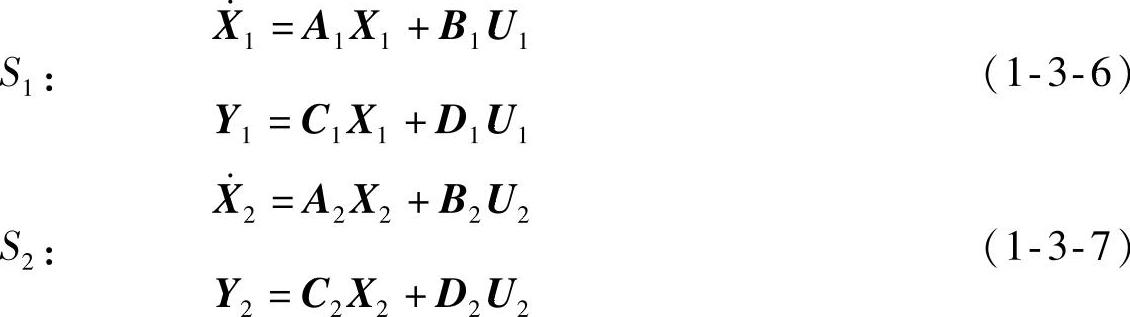
并设子系统S₁为n₁阶，含有m₁个输入，p₁个输出；即A₁为n₁×n₁方阵，B₁为n₁×m₁阵，C₁为p₁×n₁阵，D₁为p₁×m₁阵。子系统S₂为n₂阶，含有m₂个输入，p₂个输出；即A₂为n₂×n₂方阵，B₂为n₂×m₂阵，C₂为p₂×n₂阵，D₂为p₂×m₂阵。

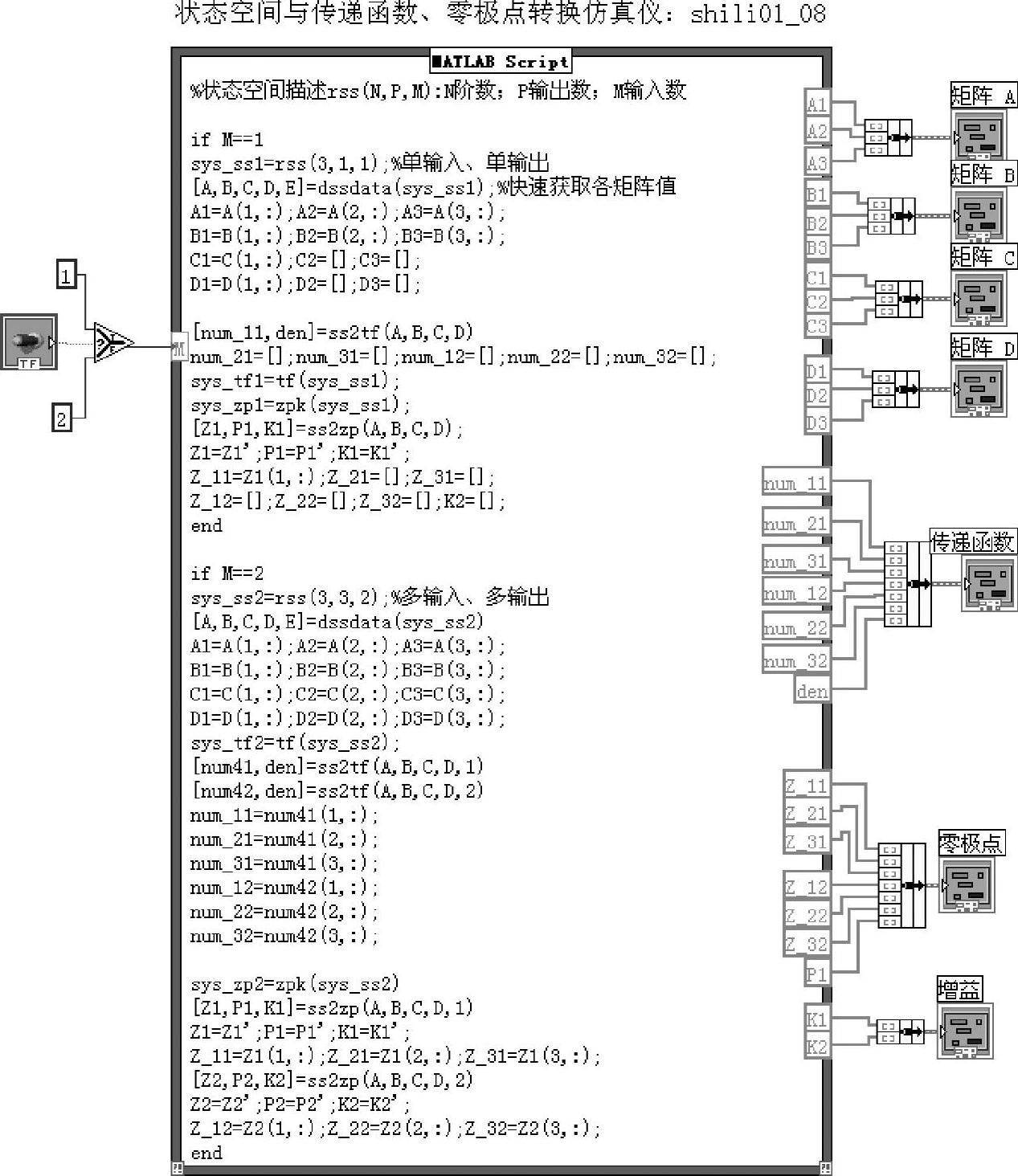
图1-3-4 程序shili01_08框图面板

1.串联

子系统S₁和子系统S₂串联的示意图如图1-3-5所示。

图1-3-5 状态空间模型串联示意图

串联系统的内部结构如图1-3-6所示。

图1-3-6 串联系统的内部结构

下面分3种情况讨论状态空间模型的串联。

（1）S₁的输出分量数等于S₂的输入分量数（p₁=m₂）

这时S₂的每一个输入都对应等于S₁的一个输出，即Y₁=U₂。串联等效系统的输入为S₁的输入U₁，输出为S₂的输出Y₂。系统的状态向量由X₁，X₂共同组成。

用式（1-3-6）中的Y₁代替式（1-3-7）中的U₂，经过简单运算可得

由式（1-3-6）和式（1-3-8）可得串联系统的状态空间模型

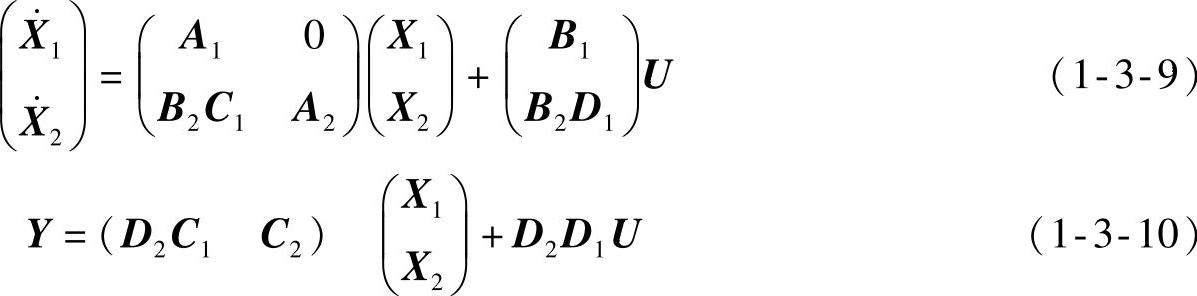
两式中U=U₁表示串联系统的输入，Y=Y₂表示串联系统的输出。

显然若式（1-3-9）和式（1-3-10）成立，必须使矩阵乘积B₂C₁、B₂D₁、D₂C₁和D₂D₁有定义，这就要求m₂=p₁。

将式（1-3-9）和式（1-3-10）改写成式（1-3-1）状态方程和输出方程的形式，可知串联系统的状态向量X有n₁+n₂个分量。系数矩阵为（n₁+n₂）×（n₁+n₂）方阵，输入矩阵有（n₁+n₂）×m₁维，输出矩阵有p₂×（n₁+n₂）维，直传矩阵有p₂×m₁维。传递函数矩阵仍有式（1-3-3）的形式，有p₂×m₁维。

对于MIMO系统，因为p₁=m₂＞1，所以S₁的p₁个输出与S₂的m₂个输入分量可以全部一一对应连接。为讨论方便，假定S₂输入分量顺序[u₁，u₂，…，u_m2]不变，通过改变S₁的输出分量顺序[y₁，y₂，…，y_p1]来改变S₁与S₂的串联方式。S₁的输出分量顺序变化有p₁阶乘（p₁！）种情况，因而串联也有p₁！种情况。以p₁=m₂=3为例，图1-3-7列出了所有的串联情况，共3！=6种。

图1-3-7 S₁输出与S₂输入的连接方式（m₂=p₁=3）

图1-3-7中的数字1、2、3分别表示S₁的输出[y₁，y₂，y₃]与S₂的输入[u₁，u₂，u₃]。例如，第⑥种情况表示S₁的输出y₂、y₁、y₃分别与S₂的输入u₁、u₂、u₃连接。由图1-3-7可见，这些连接是通过对S₁的输出序号进行全排列，而保持S₂的输入不动来实现的。S₁输出序号的全排列可以通过交换矩阵C₁和D₁的行来实现。保持S₂的输入不动就是保持矩阵B₂、D₂行列位置不动。通过这种处理，式（1-3-9）和式（1-3-10）可以涵盖所有串联方式。

MATLAB为串联提供了以下两种常用的基本函数：

函数sys1*sys2只适用于p₁=m₂的情况，故称之为“标准串联”，如图1-3-7中的第①种情况。函数series可以适用于所有串联情况。

使用“标准串联”函数除了注意p₁=m₂的基本条件之外，仿真运行时还需注意以下两点：

1）与series（sys1，sys2，outputS1，inputS2）命令等价的“标准串联”函数格式实际上是sys=sys2*sys1，即这两个命令中子系统S₁、S₂次序是颠倒的。如果要求串联连接满足两子系统可交换相乘，则使用相乘函数仿真时，“标准串联”实际上要求满足p₁=m₂和p₂=m₁。

2）仿真格式使状态向量X₁与X₂交换顺序，式（1-3-9）和式（1-3-10）更改为

一般的串联函数series（sys1，sys2，outputS1，inputS2）中，outputS1表示S₁输出量序号所构成的矢量，如[1，2，3]，[2，3，1]等，如上所述，共有3！=6种排列方式。inputS2表示S₂输入量序号所构成的矢量，只有[1，2，3]一种方式。于是，series函数的具体格式为

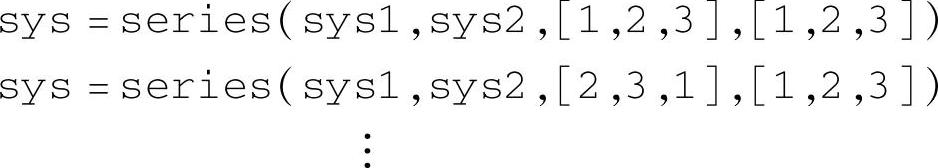
不过，不同的串联方式都具有相同的特征值。

也可以保持S₁输出量序号不变，通过改变S₂输入量序号来实现所有的串联情况。这和保持S₂输入顺序不变，改变S₁的输出顺序是等价的。不过需要注意等价与否应当从B₂C₁结果是否相同来评定。例如，图1-3-7中的第②串联方式的等价形式如图1-3-8所示。

图1-3-8 S₁输出与S₂输入连接的等价示意图

因为B₂C₁的乘积实际上是B₂的列（对应S₂的u）和C₁的对应行（对应S₁的y）相乘再求和，图1-3-8左边表示B₂的第1、2、3列对应与C₁的2、3、1行相乘后求和，简记为（12）+（23）+（31），右边B₂C₁相乘则可简记为（31）+（12）+（23），两种情况下矩阵乘积B₂C₁相同。

【例1-9】p₁=m₂时状态空间模型串联仿真分析仪。

设S₁为随机产生的三阶二输入、三输出系统，S₂为随机产生的四阶三输入、二输出系统（p₁=m₂=3）。仿真仪程序如shili01_09所示，其程序框图面板和前面板分别如图1-3-9和图1-3-10所示。

图1-3-9 程序shili01_09框图面板（p₁=m₂=3）

程序说明：

程序给出了标准串联方式，S₁输出全排列的6种串联方式的状态空间模型和对应的传递函数矩阵，给出了按式（1-3-9）和式（1-3-10）的计算结果，并对这些串联方式的结果进行比较。

运行程序，首先选择随机赋值，构造子系统S₁和S₂，然后将选择开关置于“串联连接”。再通过“连接选择”菜单选择S₁输出与S₂输入的6种连接方式，连接选择菜单如图1-3-11所示。

对应每种连接方式，前面板（见图1-3-10）同时给出了子系统S₁、S₂的各系数矩阵A₁、B₁、C₁、D₁和A₂、B₂、C₂、D₂，以及串联之后的系数矩阵A、B、C、D。对于每种串联的传递函数矩阵均有如下形式：

图1-3-10中num1的两行分别表示传递函数y₁（s）/u₁（s）和y₂（s）/u₁（s）的分子多项式系数，num2的两行分别表示传递函数y₁（s）/u₂（s）和y₂（s）/u₂（s）的分子多项式系数。所有传递函数分母多项式均相同，因为它们具有相同的特征多项式，其系数统一表示为den。

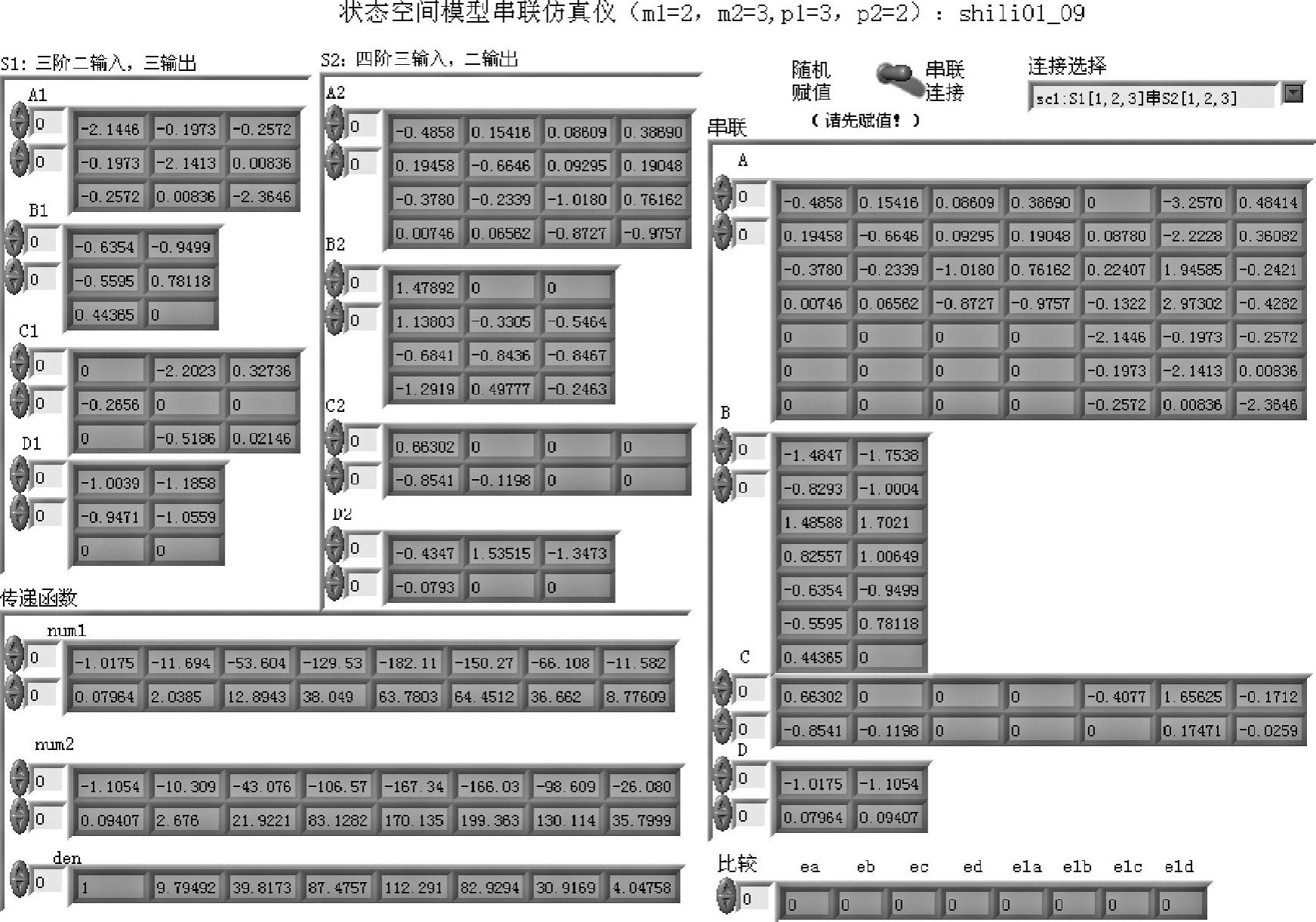
图1-3-10 程序shili01_09前面板（p₁=m₂=3）

前面板右下方最末一行数组给出了各种串联结果的比较。前4列（ea、eb、ec、ed）表示6种串联方法所得各系数矩阵，与由式（1-3-11）和式（1-3-12）所计算得出的对应矩阵的范数（norm）差。后4列（e1a、e1b、e1c、e1d）表示由s2*s1命令所得出的结果与由series函数针对图1-3-7中①运算结果的比较。仿真表明式（1-3-11）和式（1-3-12）的计算结果与series函数运行结果相同，“标准串联”仅仅与图1-3-7中的①等价，而不适用于其他排列情况下的串联。

（2）S₁的输出分量数大于S₂的输入分量数（p₁＞m₂）

连接菜单如图1-3-11所示，S₁的输出在连接S₂的所有输入后还有剩余，如图1-3-12所示。

图1-3-11 连接选择菜单

图1-3-12 p₁＞m₂的串联示意图

此时函数sys=sys1*sys2不再适用，只能使用series函数。保持分量数较少的S₂输入不动，每次从S₁的输出中取m₂个输出与S₂的全部输入串联，总共构成从p₁中取m₂的排列（A^m2_p1）种串联连接方式。例如，若p₁=3，m₂=2，则可以构成A²₃=6种串联形式，具体连接方式如图1-3-13所示。

图1-3-13 S₁输出与S₂输入的串联方式（p₁=3，m₂=2）

【例1-10】S₁输出分量数大于S₂输入分量数（p₁=3，m₂=2）的状态空间模型串联仿真仪。仿真程序如shili01_10所示，其前面板和程序框图面板分别如图1-3-14和图1-3-15所示。

程序说明：

本例p₁=3，m₂=2，不满足“标准串联”条件，只能使用series函数仿真。按图1-3-13所示，每次从S₁输出中取出两个分量与S₂的两个输入分量连接，串联语句的具体格式为

这样处理后，式（1-3-11）和式（1-3-12）仍然适用。但是由矩阵乘积构成的各块矩阵元B₂C₁、B₂D₁、D₂C₁和D₂D₁中，属于S₁的C₁和D₁将发生两点变化。第一，从原始C₁和D₁的3（p₁=3）行中取出2（m₂=2）行构成子矩阵；第二，这些子矩阵的行序需要按照图1-3-13所示的排列规律进行排列。例如，图1-3-13中的④表示取出原始C₁和D₁中的第3行构成子矩阵的第1行；取出原始C₁和D₁中的第2行构成子矩阵的第2行。这时式（1-3-11）和式（1-3-12）的程序编写如下（以④为例）：

程序中[C1（3，：）；C1（2，：）]和[D1（3，：）；D1（2，：）]分别是原始C₁和D₁在串联方式④中的子矩阵。程序的物理意义在于使S₁输出分量y₃与S₂的输入分量u₁串联，使S₁输出分量y₂与S₂的输入分量u₂串联。

每种串联后的传递函数矩阵均由2行3列组成，对应S₂的两个输出（串联系统输出）和S₁的3个输入（串联系统输入），见式（1-3-14）。图1-3-14中num1、num2和num3的两行分别表示式（1-3-14）中第1、2和第3列所示的两个传递函数的分子多项式系数。所有传递函数分母多项式均相同，因为它们具有相同的特征多项式，其系数统一表示为den。

图1-3-14 程序shili01_10前面板（p₁=3，m₂=2）

图1-3-15 程序shili01_10框图面板（p₁=3，m₂=2）

前面板右下方最末一行数组给出了各种串联结果的比较。从e_a到e_d表示6种串联方法所得各系数矩阵，与由式（1-3-11）和式（1-3-12）计算得出的对应矩阵的范数（norm）差。仿真表明，使用对应的子矩阵后，式（1-3-11）和式（1-3-12）的计算结果与series函数运行结果相同。

（3）S₁的输出分量数小于S₂的输入分量数（p₁＜m₂）

这时S₂的输入在连接了S₁的所有输出后还有剩余，如图1-3-16所示。

图1-3-16 p₁＜m₂的串联示意图

此时函数sys=sys1*sys2也不再适用，只能使用series函数。保持分量数较少的S₁输出不动，每次从S₂的输入中取p₁个输入与S₁的全部输出串联，总共构成从m₂中取p₁的排列（A^p_m12）种串联连接方式。例如，若p₁=2，m₂=3，则可以构成A²₃=6种串联形式，具体连接方式可以将图1-3-13中的输入输出交换得到，如图1-3-17所示。

图1-3-17 S₁输出与S₂输入的连接方式（p₁=2，m₂=3）

【例1-11】S₁输出分量数小于S₂输入分量数（p₁=2，m₂=3）的状态空间模型串联仿真仪。仿真程序如shili01_11所示，其程序框图面板和前面板分别如图1-3-18和图1-3-19所示。

程序说明：

本例p₁=2，m₂=3，也不满足“标准串联”条件，只能使用series函数仿真。按图1-3-17所示，每次从S₂输入中取出两个分量与S₁的两个输出分量连接，串联语句的具体格式为

可以对式（1-3-11）和式（1-3-12）进行推广，使之适用于各种串联情况。推广时，由

图1-3-18 程序shili01_11框图面板（p₁=2，m₂=3）

图1-3-19 程序shili01_11前面板（p₁=2，m₂=3）

矩阵乘积构成的各块矩阵元B₂C₁、B₂D₁、D₂C₁和D₂D₁中，属于S₂的B₂和D₂将发生两点变化。第一，从原始B₂和D₂的3（m₂=3）列中取出两（p₁=2）列构成子矩阵；第二，这些子矩阵的列序需要按照图1-3-17的规律进行排列。例如，图1-3-17中的④表示取出原始B₂和D₂中的第3列构成子矩阵的第1列；取出原始B₂和D₂中的第2列构成子矩阵的第2列。这时式（1-3-11）和式（1-3-12）的程序编写如下（以④为例）：

其中，[B2（：，3），B2（：，2）]和[D2（：，3），D2（：，2）]分别是原始B₂和D₂在串联方式④中的子矩阵。程序的意义在于使S₁的输出分量y₁与S₂的输入分量u₃串联，使S₁的输出分量y₂与S₂的输入分量u₂串联。

每种串联的传递函数矩阵均由3行2列组成（p₂=3，m₁=2），对应S₂的3个输出和S₁的两个输入，见式（1-3-15）。图1-3-19中num1和num2的3行分别表示式（1-3-15）中第1、2列所示的3个传递函数的分子多项式系数。所有传递函数分母多项式均相同，因为它们具有相同的特征多项式，其系数统一表示为den。

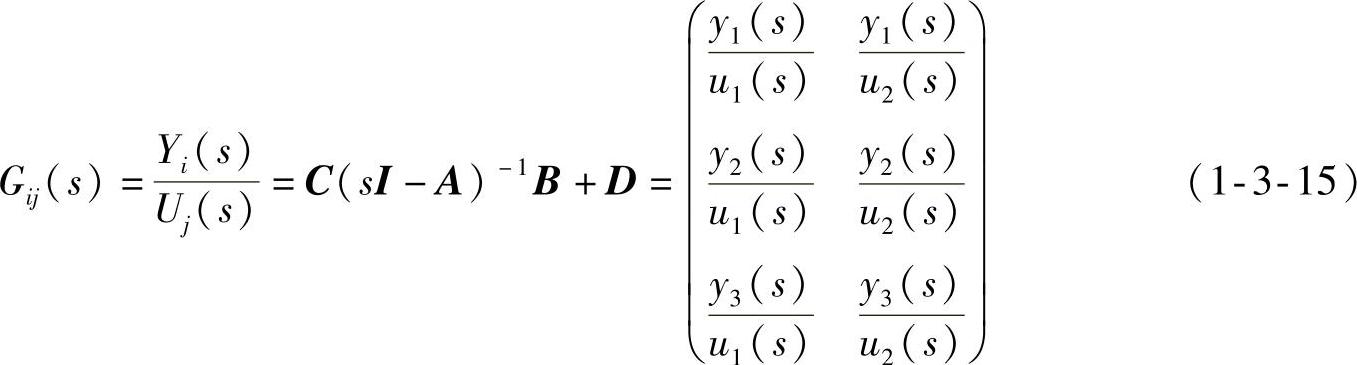
前面板右下方最末一行数组给出了各种串联连接结果的比较。从e_a～e_d表示6种串联方法所得各系数矩阵，与由式（1-3-11）和式（1-3-12）计算得出的对应矩阵的范数（norm）差。仿真表明使用对应的子矩阵后，式（1-3-11）和式（1-3-12）的计算结果与series函数运行结果相同。

2.并联

状态空间模型S₁与S₂并联的结构如图1-3-20所示。系统输入相同，即U₁=U₂=U；输出为两子系统输出的代数和，Y=Y₁+Y₂。

MATLAB为并联连接提供了如下两种常用的基本函数：

其中，input1、input2分别表示S₁与S₂相互连接的输入分量序号矢量；output1、output2分别表示S₁与S₂相互叠加的输出分量序号矢量。

因此，parallel函数包括并联时输入、输出的各种不同的连接方式，而sys1+sys2只包含一种连接方式。

下面分两种情况讨论状态空间模型的并联。

图1-3-20 状态空间模型S₁与S₂的并联结构

（1）S₁与S₂的输入分量数和输出分量数分别相等（m₁=m₂，p₁=p₂）

将U₁=U₂=U和Y=Y₁+Y₂代入式（1-3-6）和（1-3-7）中有

由矩阵的性质可知，欲使式（1-3-16）和式（1-3-17）成立，则要求B₁和B₂有相同的列数，C₁和C₂有相同的行数，D₁和D₂有相同的行、列数。也就是说，式（1-3-16）和式（1-3-17）所描述的状态空间模型并联，仅限于参与并联的两子系统具有相同的输入分量数和相同的输出分量数的情况。当满足这个条件时，才构成状态空间模型的“标准并联”。“标准并联”的基本特征是相同序号的输入并联，相同序号的输出叠加，不考虑“交叉”连接情况，如图1-3-21所示。

图1-3-21 输入、输出数分别相等的并联示意图

显然，如果考虑“交叉”连接情况，输入的连接方式有A^m_m11种，输出的连接方式有A^p_p11种，并联方式有种。以m₁=m₂=2，p₁=p₂=3为例，输入并联的A²₂=2方式如图1-3-22所示。

图1-3-22 S₁与S₂输入的并联连接方式（m₁=m₂=2）

输出叠加的A³₃=6种方式如图1-3-23所示。图中的加号表示S₁与S₂输出对应分量的代数和。

考虑输入输出连接的组合后，并联方式有A²₂×A³₃=12种。语句sys1+sys2仅描述图1-3-22和图1-3-23中的第①1号组合，所有并联情况均可使用parallel函数。

图1-3-23 S₁与S₂输出的叠加方式（p₁=p₂=3）

【例1-12】状态空间模型并联仿真仪。

设子系统S₁为三阶二输入三输出，子系统S₂为二阶二输入三输出。仿真程序如shili01_12所示，其程序框图面板和前面板分别如图1-3-24和图1-3-25所示。

图1-3-24 程序shili01_12框图面板（m₁=m₂=2，p₁=p₂=3）

程序说明：

子系统S₁、S₂均有两个输入，并联时可以将两者同序号的输入相连（u₁₁接u₂₁，u₁₂接u₂₂），也可以将两者输入交叉相连（u₁₁接u₂₂，u₁₂接u₂₁），分别如图1-3-22的①和②所示。S₁、S2子系统的3个输出叠加的6种方式如图1-3-23所示。以图中的叠加③为例，表示S₁的输出y₁₁、y₁₂、y₁₃分别与S₂的y₂₃、y₂₁、y₂₂对应叠加，构成并联后的系统输出y₁、y₂和y₃。对图1-3-22的输入连接与图1-3-23的输出叠加组合的A²₂×A³₃=12种并联方式，使用并联命令parallel的具体书写格式为（以图1-3-22和图1-3-23的组合①3为例）

其余11种并联方式可以依此类推。

前已述及，标准并联命令sys1+sys2只描述相同序号输入、输出对应连接的情况，其等价parallel语句为

图1-3-25 程序shili01_12前面板（m₁=m₂=2，p₁=p₂=3）

12种并联方式对应12个传递函数矩阵。各传递函数矩阵均为3×2维，见式（1-3-15）。各传递函数分子多项式语句如图1-3-24中的n111、n112…所示，结果如图1-3-25中的num1和num2所示，分别对应由并联后系统的输入1、输入2与3个输出所构成的传递函数。所有传递函数具有共同的特征矩阵，其特征多项式系数用den表示。

运行程序，先选择随机赋值，再选择并联方式。12种并联方式由图1-3-26所示的连接选择菜单给出。

图1-3-26 输入数与输出数分别相等的并联方式连接选择菜单（m₁=m₂=2，p₁=p₂=3）

式（1-3-16）和式（1-3-17）只适用于标准并联情况，但进行推广后可适用于所有并联方式。仍取图1-3-22的①和图1-3-23的3组合①3为例，对比一下该组合与①1组合可知，两者只是S₂的输出序号不同，也就是S₂的输出矩阵C₂的行改变了顺序，式（1-3-16）和式（1-3-17）所给出的各系数矩阵可以写成

上述语句是按照图1-3-23的3重新排列C₂与D₂的各行构成的。需要注意的是，当输入连接变成图1-3-22的②时，矩阵B₂和D₂的列顺序需要进行相应的排列。以图1-3-22的②和图1-3-23的3组合②3为例，程序如下：

先对矩阵D₂进行列排列，演变成D_2，再对D_2实施行排列。这表明，输入顺序的改变导致输入矩阵B和直传矩阵D的列顺序改变；输出顺序的改变导致输出矩阵C和直传矩阵D的行顺序改变。进行这种列、行顺序变更后，式（1-3-16）和式（1-3-17）将适用于所有并联情况。

再仔细分析图1-3-23中S₂输出分量的各种叠加方式，可以发现这6种叠加方式（也就是6种并联方式）并非各自独立，其中的叠加方式4、5和6可以由叠加方式1、2和3通过适当的行序重排构成。例如，叠加4的第1行、第2行和第3行可以分别由叠加1的第1行、叠加2的第2行和叠加3的第3行组合构成。这种非独立性既反映在对式（1-3-16）和式（1-3-17）的修正和推广上，也反映出在同一种输入连接情况下（例如图1-3-22的①），这6种并联方式所对应的传递函数矩阵不是独立的。以并联方式①4的传递函数矩阵为例（参见式（1-3-15）），其第1、第2和第3行分别等于并联①1、①2和①3的传递函数矩阵的第1行、第2行和第3行。在程序中描述为n141的3行分别等于n111的第1行、n121的第2行和n131的第3行，即n141（1，：）=n111（1，：），n141（2，：）=n121（2，：），n141（3，：）=n131（3，：）。叠加方式5和6也有类似情况。于是，对于本例，12个传递函数矩阵只有6个是独立的，72个传递函数只有36个是独立的。仿真结果证实了这种分析的正确性。

前面板的右下角比较数组给出了两部分的比较结果。前4个表示使用更改后的公式与对应的parallel语句运行结果的比较，ea、eb、ec和ed分别表示系统矩阵、输入矩阵、输出矩阵和直传矩阵的比较结果。后3个（en1，en2，en3）表示对于相同输入方式，叠加方式4、5和6所构成的传递函数矩阵与用叠加方式1、2和3所构成的传递函数矩阵各行的比较。这3个比较只针对①4、①5、①6和②4、②5、②6，其中①4组合与①1、①2、①3组合的传递函数矩阵的仿真数据如图1-3-27所示。

要强调的是，由sysb=s_ss1+s_ss2构成的标准并联只要求两个子系统的输入分量数、输出分量数分别相等，不要求输入和输出分量数相等，也不要求子系统阶数相同。在构成标准并联结构图时，两子系统相同序号的输入相连，相同序号的输出相叠加，不考虑交叉输入连接和交叉输出叠加的情况。

（2）S₁与S₂的输入分量数和输出分量数均不相等（m₁≠m₂，p₁≠p₂）

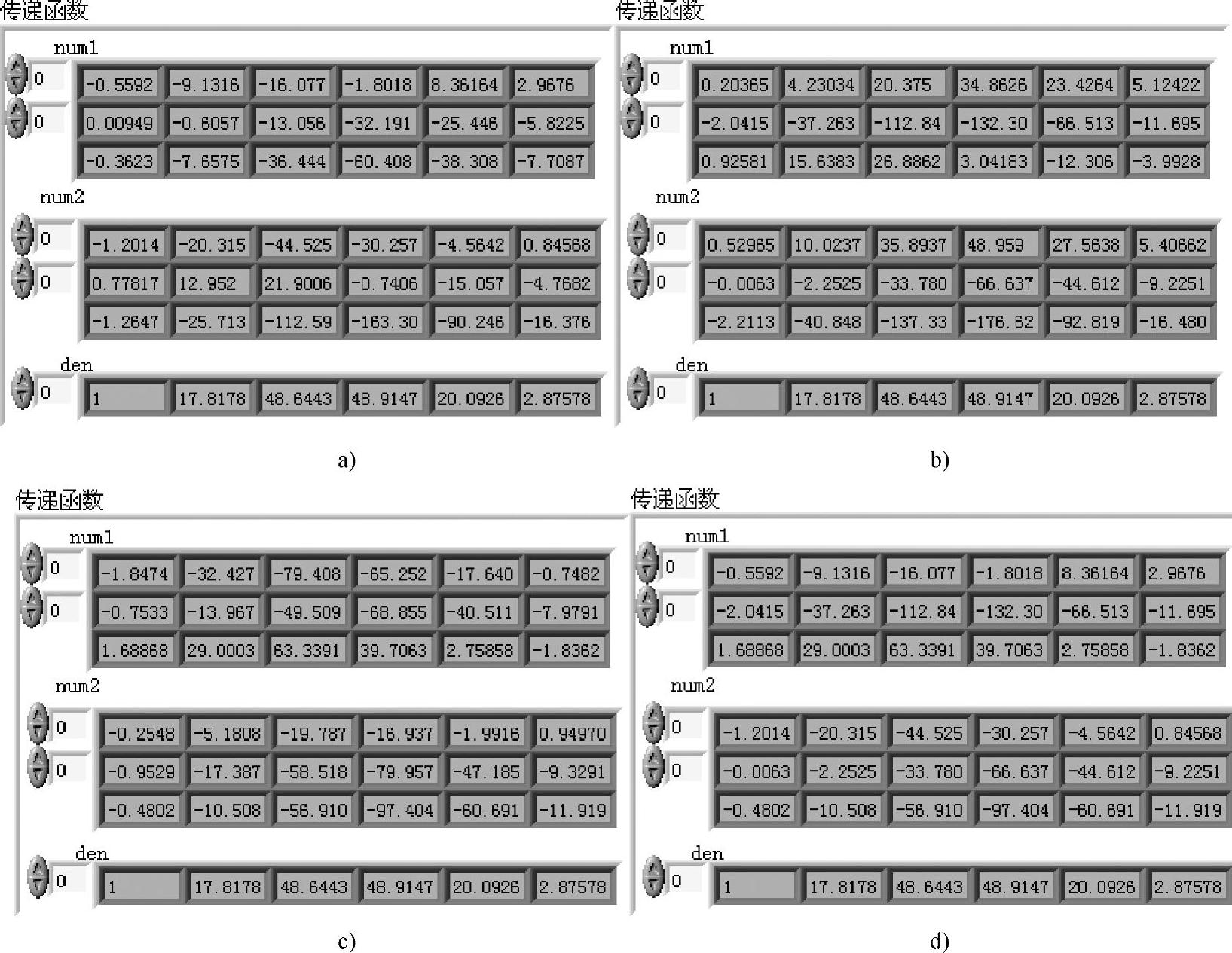
图1-3-2 7并联①4与并联①1、①2、①3传递函数矩阵的仿真数据

a）并联①1（sb11） b）并联①2（sb12） c）并联①3（sb13） d）并联①4（sb14）

下面讨论处理这类并联问题的两种方法，即直接并联法和“零列零行补偿”并联法。首先讨论直接并联法。

为讨论方便，假定m₁＞m₂，p₁＜p₂，并联示意如图1-3-28所示，输入并联有A^m2_m1种方式，输出叠加有A^p1_p2种方式，共有A^m2_m1×A^p1_p2种方式。例如，设m₁=3，m₂=2；p₁=2，p₂=3，则输入连接时固定S₂的两个输入不变，每次从S₁的3个输入中取两个与之连接，如图1-3-29所示。

图1-3-2 8输入、输出数均不相等的并联连接示意图（m₁＞m₂，p₁＜p₂）

图1-3-29 S₁与S₂的输入连接方式（m₁=3，m₂=2）

对于输出叠加，由于p₁=2，p₂=3，固定S₁的两个输出不变，每次从S₂的3个输出中取两个分别与之叠加，如图1-3-30所示。

图1-3-30 S₁与S₂的输出叠加方式（p₁=2，p₂=3）

【例1-13】状态模型的直接并联仿真仪。

设子系统S₁为三阶三输入二输出，子系统S₂为二阶二输入三输出。仿真程序如shili01_13所示，其程序框图面板和前面板分别如图1-3-31和图1-3-32所示。

图1-3-31 程序shili01_13框图面板(www.xing528.com)

程序说明：

将图1-3-29与图1-3-30共同组合成直接并联，一共可以获得36种状态空间模型，也就有36个传递函数矩阵，每个传递函数矩阵由3个输入和3个输出构成，共有324个传递函数，这些模型的构成方式是相似的。为简化计算，选取图1-3-29的每种输入连接与图1-3-30中的两种输出叠加相组合，构成①1，①3；②2，②4；…；⑤5，⑤1和⑥6，⑥2等12种并联结构。

12种并联方式对应12个传递函数矩阵。由于并联后系统有3个输入和3个输出，所以各传递函数矩阵均为3×3维，见式（1-3-18）。各传递函数分子多项式语句如图1-3-31中的n111，n112，…所示，仿真结果如图1-3-32中num数组的9行所示。这9行从上到下每3行为一组，顺次表示由输入1、2、3分别与3个输出所构成的传递函数，依次对应式（1-3-18）的第1、第2和第3列。所有的传递函数阵具有共同的特征矩阵，其特征多项式系数用den表示。

图1-3-32 程序shili01_13前面板

运行程序，先选择随机赋值，再选择并联方式。12种并联方式由图1-3-33所示的连接选择菜单给出。

下面讨论如何修改式（1-3-16）和式（1-3-17），使之适用于直接并联的各种方式。以图1-3-29和图1-3-30的组合②4为例，求出并联后的各系数矩阵的表达方法。

输入矩阵B中原矩阵B₁的列顺序需要改变。由于m₁＞m₂，B₂需要添加适当的0元素列，使之与B₁的列数相同。

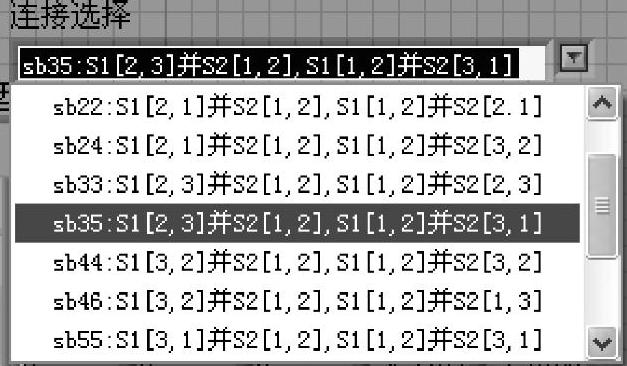
图1-3-33 输入、输出分量数不同的直接并联方式连接选择菜单

例如，图1-3-29中的②，表示从S₁的3个输入中选取第2和第1两个输入参与连接，剩余的第3输入“空闲”。MATLAB将该“空闲”输入视为并联系统的第一输入，所以在构成并联输入矩阵时，将“空闲”输入所对应的列（第3列）置于首列，其余按所选取输入的顺序（第2、第1）放置所对应的列（第2列、第1列）。于是，对所有输入连接为②的输入矩阵均可表示为

并联方式②4仿真运行后输入矩阵B的构成如图1-3-34所示。

图1-3-34 直接并联方式②4的输入矩阵构成

显然，输入矩阵B的构成仅与图1-3-29中的输入连接方式有关，与图1-3-30的输出叠加方式无关。上述构成方法适用于图1-3-29中所有输入连接方式，构造方法思路具有普遍性。

输出矩阵C的构成仅与图1-3-30的输出叠加方式有关。由于p₁＜p₂，C₁需要添加适当的0元素行，使之与C₂的行数相同。C₂的行顺序需要改变。MATLAB将S₂中未参与叠加的“空闲”输出视为并联系统的最末尾输出。因此，须将该“空闲”输出所对应的行置于末行，其余按所选取输出的顺序放置所对应的行。例如，对于图1-3-30的叠加方式4，其参与叠加的输出依次为第3和第2输出，第1输出“空闲”，所以并联后的输出矩阵C中，C₂依次由原来的第3、第2和第1行构成，C₁的第3行为添加的0元素行。于是对所有输出叠加为4的输出矩阵均可表示为

此语句也可写成

并联方式②4仿真运行后输出矩阵C的构成如图1-3-35所示。

根据同样方法，不难得出图1-3-30的其他叠加方式中输出矩阵C的构成方法。

要使并联后的直传矩阵D=D₁+D₂适用于两子系统输入数和输出数不等的情况，必须解决两个问题。第一，必须使原系统的D₁和D₂维数相容。这可以通过对D₁添加0元素行，对D₂添加0元素列，使之均为3行3列来解决。具体操作时，添加到D₁的第3行为0元素行，表示对S₁添加的第3输出为0，不影响S₁的实际输出；添加到D₂的第1列为0元素列，表示对S₂添加的第1输入为0，也不影响S₂的实际输入。第二，必须使D₁的列顺序符合图1-3-29中S₁输入的排列。因为对于S₂的输入选取是不变的，所以D₂的列顺序是不变的。同理，应当使D₂的行顺序符合图1-3-30中S₂输出的排列，不需要改变D₁的行顺序。具体操作时，使D₁的列顺序排列与B₁的列顺序相同，使D₂的行顺序排列与C₂的行顺序相同。并联方式②4的直传矩阵构成语句为

图1-3-35 并联方式②4的输出矩阵C的构成

并联方式②4仿真运行后，直传矩阵D的构成如图1-3-36所示。

图1-3-36 直接并联方式②4的直传矩阵D的构成

用上述方法修改式（1-3-16）和式（1-3-17）后，计算出各种并联的系数矩阵与使用parallel函数所获得的对应结果相同。图1-3-32中右下角显示出了这两种方式的比较结果。

直接并联的传递函数矩阵具有下列特点：

1）对于所有并联方式，传递函数G₃₁（s）=y₃（s）/u₁（s），即式（1-3-18）第3行第1列元素总等于零。这是因为，在传递函数矩阵的计算式C（sI-A）^-1B+D中，输出矩阵C第3行（末行）的前3列都是0（见图1-3-35）。特征矩阵逆的最后两行（第4、第5行）的前3列都是0（见图1-3-32中的矩阵A）。输入矩阵B的最后两行（第4、第5行）的第1列也是0（见图1-3-34），它们乘积使得第3行第1列为0。而直传矩阵的第3行第1列为0（D₁的3行全0，D₂的第1列全0，二者第1列之和保证第3行第1列为0），所以最后使得y₃（s）/u₁（s）=0。

2）如果将传递函数分子多项式系数记为n_ijk，其中i、j=1，2，…，6，分别表示图1-3-29和图1-3-30的输入、输出连接方式；k=1，2，3表示并联后传递函数的输入序号，则n_ijk将表示传递函数矩阵的某一列。如果将输入连接分成i=1，2；i=3，4；i=5，6这样3组，每组输入的差别仅是S₁的两个输入交换顺序。在同一组输入连接与所有输出叠加组合中，输入1（k=1）的三个传递函数均相等，即（n_1j1，n_2j1）、（n_3j1，n_4j1）和（n_5j1，n_6j1）三组中各对应元素相等。也就是说，同一组输入连接与6种输出叠加所构成的12个传递函数矩阵中，第1列各元素对应相等，见式（1-3-18）。这是因为，对同一组输入连接，并联后输入矩阵B的第一列相同，特征矩阵及其逆阵相同，所以特征矩阵的逆阵与输入矩阵B相乘后的第一列相同，而对于同一组输入连接的输出矩阵C又是相同的，再加上对同一输入组，矩阵D的第一列构成相同，对传递函数矩阵的第一列贡献也相同，所以对于同一组输入，乘积C（sI-A）^-1B+D的第一列相同。

在例1-13中，分别运行[sb11，sb13，sb22，sb24]（输入i=1，2）、[sb33，sb35，sb44，sb46]（输入i=3，4）和[sb55，sb51，sb66，sb62]（输入i=5，6）三组四种连接。仿真结果表明，各组4个传递函数矩阵的首列（即图1-3-32传递函数数组的前3行）对应相等，如图1-3-37所示。第一组各相等首列所对应分子多项式系数为（n111，n131，n221，n241），其余两组相等首列所对应分子多项式系数可以依此类推。

3）如果将输出叠加分成j=1，2；j=3，4；j=5，6这样3组，每组输出叠加的差别仅是S₂的两个输出交换了顺序。在同一组输出叠加与所有输入组合中，输出3对三个输入的传递函数均相等。也就是说，同一组输出叠加与6种输入方式所构成的12个传递函数矩阵中，第3行各元素对应相等，见式（1-3-18），即（n_i1k（3，：），n_i2k（3，：））、（n_i3k（3，：），n_i4k（3，：））、（n_i5k（3，：），n_i6k（3，：））三组中各对应元素相等。这是因为，对同一组输出叠加，输出3是S₂的“空闲”输出，而对同一组而言，S₂的“空闲”输出是相同的，它们对3个输入构成的传递函数位于式（1-3-18）的第3行，对每组都是相同的。

按输出叠加方式查看图1-3-37中[sb11，sb22，sb51，sb62]（输出j=1，2）、[sb13，sb24，sb33，sb44]（输出j=3，4）和[sb35，sb46，sb55，sb66]（输出j=5，6）三组四种连接，它们对应的传递函数数组的第3、6、9行，构成各传递函数矩阵的第3行对应相等。例如，图1-3-37中sb11的第3，6，9行，对应传递函数分子多项式系数为（n111（3，：），n112（3，：），n113（3，：））。sb11与sb22传递函数矩阵的第3、6、9行对应相等，实际上表示n111（3，：）=n221（3，：），n112（3，：）=n222（3，：）和n113（3，：）=n223（3，：）三个传递函数分子多项式系数相等。其余相等情况可以依此类推。由于仿真仪是随机赋值，所示具体数据仅对某次运行有效。

程序shili01_13a、shili01_13b和shili01_13c所示的并联仿真仪，输入输出方式及程序编写不同，列出供参考。

下面讨论“零列零行补偿”并联法。

上面讨论的直接并联法，虽然可以解决m₁≠m₂，p₁≠p₂的一般并联问题，但在修改式（1-3-16）和式（1-3-17）适于非标准并联情况时比较复杂，对于不同的输入输出组合所得到的仅是形式相同的公式。公式中各项需要随着输入/输出的不同组合而重新构造。下面介绍的“零列零行补偿”并联法实际上是一种“添加0输入（出）补偿法”，将非标准并联纳入标准并联方式解决的方法。

“零列零行补偿”并联法的基本做法是对输入数量较少的子系统，将其输入矩阵B添加若干元素全为0的列，以满足条件m₁=m₂；类似地，将输出分量数较少的子系统的输出矩阵C添加若干元素全为0的行，以满足条件p₁=p₂，同时对直传矩阵进行类似的0元素行、列添加，以满足标准并联条件。

图1-3-37 直接并联法输入、输出组合的仿真数据截图

图1-3-37 直接并联法输入、输出组合的仿真数据截图（续）

【例1-14】零列零行补偿法并联仿真仪。

设子系统S₁为三阶三输入三输出，设子系统S₂为二阶二输入二输出。研究S₁与S₂并联的状态空间模型及传递函数矩阵。

采用“零列零行补偿”并联法将S₂改造成“伪”二阶三输入三输出系统，以便和S₁构成标准并联连接，如图1-3-38所示。

图1-3-38 零列零行补偿并联法示意图

仿真程序如shili01_14所示，其程序框图面板和前面板分别如图1-3-39和图1-3-40所示。

图1-3-39 程序shili01_14框图面板

系统随机产生子系统S₁：三阶三输入三输出，S₂：二阶二输入二输出。通过添加0元素行和0元素列，即程序中B2→B_2，C2→C_2，D2→D_2，由（A2，B_2，C_2，D_2）构成“伪”S₂与S₁进行标准并联，采用标准并联命令得到并联状态空间模型（Ab，Bb，Cb，Db）。如此并联后得到传递函数矩阵式（1-3-19）。

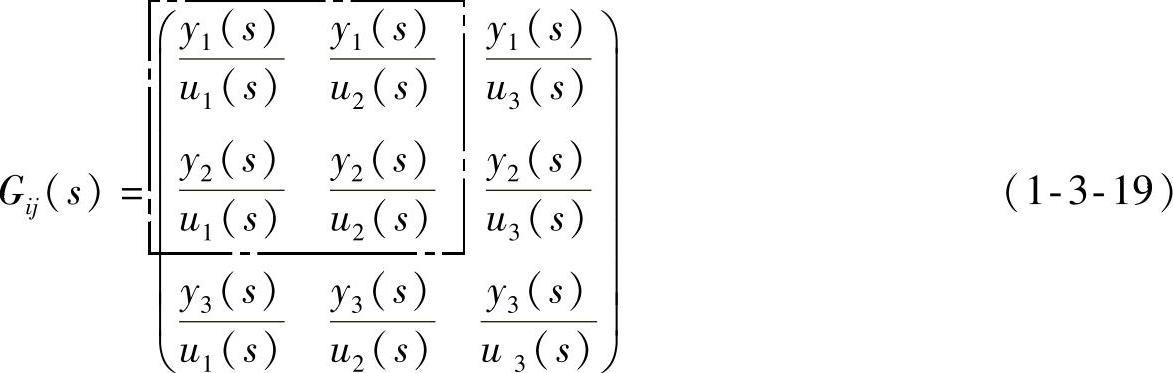
式（1-3-19）左上角的二阶方阵，是原系统S₁和S₂按照标准并联方式连接所获得的传递函数阵，如图1-3-38所示输入/输出连接的实线部分。它们的多项式系数对应表示为（见图1-3-40）。

图1-3-40 程序shili01_14前面板

通过“伪”S₂与S₁构成标准并联的程序段如下：

%状态空间模型并联“零列零行补偿法”

式（1-3-20）的传递函数是S₁的输入1对输出1的传递函数，与S₂输入1对输出1的传递函数的并联。这种子系统传递函数的简单并联关系可以表示成S₁（1，1）//S₂（1，1）。类似地，式（1-3-21）～式（1-3-23）的子系统传递函数并联关系可以分别表示成（S₁（1，2）//S₂（1，2），（S₁（2，1）//S₂（2，1），（S₁（2，2）//S₂（2，2）。程序对状态空间并联和子系统传递函数并联两种方法的结果进行了比较。由于传递函数矩阵有相同的特征多项式den，所以两种并联构成的传递函数之差就是各对应分子多项式的差，这个误差用ef表示，示于前面板并联板块的右下角，数量级为10^-15，是由计算累积误差所致。

以式（1-3-22）为例，其传递函数构成语句为

系数组

当此程序运行后，可得结果为

式（1-3-19）中其余5个传递函数都与图1-3-38的y₃和u₃有关。由于子系统S₂的y₃和u₃均为0，所以这几个传递函数完全由S₁的对应输出与输入决定，其分子多项式系数分别由num3、num6、num7、num8和num9表示。需要注意的是，它们在和den构成传递函数时，还可以进行零极点对消化简。

3.反馈

设前向通道子系统S₁，反馈通道子系统S₂构成闭环系统，参考输入为R，系统的输出为Y，如图1-3-41所示。

图1-3-41 状态空间模型的反馈链接

图中，Y₁=U₂，U₁=R-Y₂。由S₁、S₂的动态方程可以解出U₁，则

将式（1-3-24）分别代入S₁、S₂的动态方程式（1-3-6）和式（1-3-7）中，并令Z=（I+D₂D₁）-1，则可得到

综合式（1-3-25）、式（1-3-26）和式（1-3-27），考虑到闭环系统的输出是Y₁，则该系统的动态方程为

显然，如果子系统的直传矩阵D₁=D₂=0，有Z=I，则式（1-3-28）和式（1-3-29）将化简成

这是许多文献常常讨论的情况。

下面分两种情况讨论状态空间模型的反馈连接方式。

（1）p₁=m₂，p₂=m₁

S₁的输出、输入分量数分别等于S₂的输入、输出分量数。

这种情况下，子系统S₁和S₂满足式（1-3-28）和式（1-3-29），称这样的反馈连接为“标准反馈”。与标准并联类似，标准反馈只考虑“同序号”连接，即S₁的各输出分量接S₂相同序号的输入，S₂的各输出分量通过参考输入R接S₁相同序号的输入。“标准反馈”的函数调用格式为

显然，如果考虑“交叉”连接情况，S₁的输出接S₂的输入有p₁！种连接方式，S₂的输出接S₁的输入有m₁！种方式，二者组合后共有m₁！×p₁！种反馈连接方式。

以m₁=p₂=2，p₁=m₂=3为例，S₂输出接S₁输入的连接方式如图1-3-42所示。

图1-3-42 反馈中S₂输出接S₁输入的连接方式（m₁=p₂=2）

S₁输出接S₂输入的连接方式如图1-3-43所示。

图1-3-43 反馈中S₁输出接S₂输入的连接方式（p₁=m₂=3）

考虑图1-3-42与图1-3-43组合后，反馈连接方式有2！×3！=12种。函数feedback（s1，s2）仅描述图1-3-42和图1-3-43中的第①1号组合。

所有反馈连接方式可使用更一般的函数：

其中，向量feedin用于规定进入反馈环的S₁的输入序号数组，如图1-3-42中的S₁：u所示；向量feedout用于规定进入反馈环的S₁的输出序号数组，如图1-3-43中的S₁：y所示。例如，反馈方式①4的语句格式为

其余11种反馈方式的语句格式可以依此类推。

【例1-15】状态空间标准反馈连接仿真分析仪。

设子系统S₁为三阶二输入三输出，子系统S₂为二阶三输入二输出，仿真分析仪程序如shili01_15所示，程序框图面板和前面板分别如图1-3-44与图1-3-45所示。

程序说明：

程序使用了前述的两种反馈命令，并对式（1-3-28）和式（1-3-29）进行了推广。

式（1-3-28）和式（1-3-29）只适用于标准反馈①1组合，但经过更改可以推广到适用于本例的其余反馈方式。调整的基本依据是输入顺序的改变导致输入矩阵B和直传矩阵D的列顺序改变；输出顺序的改变导致输出矩阵C和直传矩阵D的行顺序改变。以反馈方式①4为例，它与组合①1的区别仅在于S₁的输出序号不同，也就是S₁的输出矩阵C₁和直传矩阵D₁的行改变了顺序。式（1-3-28）和式（1-3-29）所给出的各系数矩阵可以写成

图1-3-44 程序shili01_15框图面板（m₁=p₂=2，p₁=m₂=3）

图1-3-45 程序shili01_15前面板（m₁=p₂=2，p₁=m₂=3）

在组合①4各系数矩阵的更改公式中，除计算中需要按图1-3-43之4更改C₁和D₁的行之外，在获得了反馈系统的输出矩阵与直传矩阵之后，还需要对其分别实施行序调整。组合①与图1-3-43的其余5种组合的情况类似。

当反馈方式变成组合②4时，与组合①4的区别在于S₁的输入序号不同，也就是S₁的输入矩阵B₁和直传矩阵D₁的列改变了顺序。在组合①4指令的基础上，再加入B₁和D₁的列顺序调整，可将组合②4各系数矩阵构成指令写为

对比组合①4与组合②4，除S₁的输入（B₁）和直传矩阵（D₁）的列序发生了改变之外，反馈系统的输入矩阵（Bg₂₄）和直传矩阵（Dg₂₄）列序也发生了对应的改变。特别是直传矩阵Dg₂₄既要按组合①4更改行序，又要按②更改列序。组合②与图1-3-43的其余5种组合的情况类似。

仿真仪将由公式计算的各种反馈连接的系数矩阵与由feedback函数所获得的对应矩阵进行了对比，各矩阵差的范数在10^-15量级，示于图1-3-45右下角的“比较”数组之中，再一次示于图1-3-46，表明两种方法的结果是一致的。

图1-3-46 公式计算与feedback函数结果比较

图中，ea、eb、ec和ed分别表示两种方法所得的状态矩阵、输入矩阵、输出矩阵和直传矩阵的比较结果。值得注意的是，在反馈连接①2和①3组合中，输出矩阵Cg₁₂、Cg₁₃和直传矩阵Dg₁₂、Dg₁₃的最后行序和图1-3-43相比正好是互换的。

标准反馈连接只要求m₂=p₁，p₂=m₁，对S₁与S₂的阶数没有要求。在任何情况下，反馈连接后系统sys的输入数和输出数都与子系统S₁相同，阶数为S₁与S₂阶数之和（见图1-3-45的右部），所以传递函数矩阵有p₁×m₁维（本例为3×2维）。由子系统S₁与S₂通过上述各种反馈方式所构成的闭环系统各自独立，其对应的传递函数矩阵也是独立的。传递函数矩阵示于图1-3-45左下部的“传递函数”簇中，den数组表示该传递函数矩阵各元分母多项式系数，num1、num2各行数组分别表示输入1和输入2对3个输出所构成的传递函数分子多项式系数。

程序shili01_15a给出手动赋值的标准状态反馈连接，可供参考。

（2）p₁≠m₂，p₂≠m₁

S₁的输出、输入数不等于S₂的输入、输出数。

实际上，由于反馈连接要求S₂的所有输入和输出都应参与反馈，且分别等于所取的S₁的输出和输入，所以只有p₁＞m₂，m₁＞p₂，而没有相反的情况。也就是说，对于一般反馈连接，S₁的输出、输入数分别大于S₂的输入、输出数。S₁的部分输出反馈连接到S₂的输入，S₂的所有输出与S₁的部分输入连接，示意图如图1-3-47所示。

图1-3-47 一般反馈连接示意图

相应的反馈函数只能使用命令

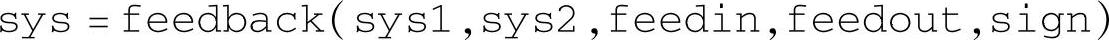
其中，向量feedin用于规定进入反馈环的S₁的输入序号，如图1-3-47中的U所示；向量feedout用于规定进入反馈环的S₁的输出序号，如图1-3-47中的Y所示。反馈连接后系统sys的输入数和输出数都与子系统S₁相同，阶数为S₁与S₂阶数之和。由于S₂的所有输入和输出都参与反馈，且分别等于所选取的S₁的输出数和输入数，于是feedin中数组的维数由S₂的输出数决定，feedout中数组的维数由S₂的输入数决定。

【例1-16】状态空间一般反馈连接仿真分析仪。

设子系统S₁为三阶三输入三输出（p₁=m₁=3），子系统S₂为二阶二输入二输出（p₂=m₂=2），研究S₂作为反馈系统的状态空间反馈连接。

由于S₁的输出数不等于S₂的输入数，S₁的输入数也不等于S₂的输出数，所以这种反馈连接必须指定参与反馈的输入/输出序号所构成的数组。向量feedin可以这样构成：固定S₂的两个输出不变，每次从S₁的3个输入中取两个与之连接，构成A^p2_m1=6种方式，如图1-3-48所示。向量feedout的构成方式如图1-3-49所示，固定S₂的两个输入不动，每次从S₁的3个输出中取两个与之连接，有A^m2_p1=6种方式，组合图1-3-48和图1-3-49的各种情况共构成36种反馈连接。

图1-3-48 反馈连接中向量feedin的构成方式（m₁=3，p₂=2）

图1-3-49 反馈连接中向量feedout的构成方式（p₁=3，m₂=2）

仿真仪程序如shili01_16所示，程序框图面板和前面板分别如图1-3-51和图1-3-52所示。

程序说明：

为了简洁起见，仿真仪只给出了①1，①4；②2，②5；③3，③6；④4，④1；⑤5，⑤2；⑥6，⑥3等12种反馈连接。框图采用选择结构，连接选择菜单如图1-3-50所示。

运行程序，先随机赋值，构建系统S₁和S₂，再由选择连接菜单选择反馈连接方式。反馈后闭环系统的各系数矩阵示于图1-3-52中反馈系统板块，反馈系统为五阶三输入三输出系统。系统阶数为S₁与S₂阶数之和，输入、输出数均等于S₁的输入输出数。相应的传递函数矩阵为3×3维，示于该图的传递函数板块。num1、num2和num3分别为一种反馈系统的3个输入与3个输出所构成的传递函数分子多项式系数，分别对应式（1-3-18）的3列。同一种反馈连接所构成的系统，传递函数矩阵具有相同的特征多项式，其系数由den表示。

图1-3-50 反馈连接的连接选择菜单

下面结合反馈连接⑥3（见图1-3-48、图1-3-49和图1-3-51），介绍对于一般反馈系统，式（1-3-28）和式（1-3-29）的推广步骤。

第1步：通过添加适当的零元素列与行，将反馈通道子系统S₂的输入矩阵B₂、输出矩阵C₂、直传矩阵D₂分别对应扩充成与B₁、C₁、D₁同维的矩阵。

图1-3-51 程序shili01_16框图（p₁=m₁=3，p₂=m₂=2）

第2步：重新排列B₁、D₁和C₁的列与行。根据图1-3-48所示的⑥重新排列B₁和D₁的列，未被选取的空闲列置于其后。重排后B₁和D₁的列序均由原始的[1 2 3]变成[1 3 2]。如果空闲列不止一个，可以依次置于后列。例如，若S₁有4个输入，则B₁和D₁的列序由[ 1 2 3 4]变成[1 3 2 4]。根据图1-3-49所示的3重新排列D₁和C₁的行，空闲行置于后行。重排后，D₁和C₁的行序均由原始的[1 2 3]变成[2 3 1]。类似地，可以重排更多的空闲行。

图1-3-52 程序shili01_16的前面板（p₁=m₁=3，p₂=m₂=2）

第3步：构成式（1-3-28）和式（1-3-29）的推广形式。由于形成公式的过程中已对B₁、D₁和C₁进行过列与行的重排，所以在获得反馈系统的输入矩阵（Bg₆₃）、输出矩阵（Cg₆₃）和直传矩阵（Dg₆₃）时需要进行还原的行列重排。还原的行列重排是指将已经更改后的行列序还原成[1 2 3]行或列。例如，对于当前的[1 3 2]列序再经过[1 3 2]的重排可以还原成[1 2 3]的列序；而对于当前[2 3 1]的行序则需经过[3 1 2]的重排才可以还原成原始的[1 2 3]行序。因此，程序中Bg₆₃、Dg₆₃的列应再次进行[1 3 2]重排；而Cg₆₃和Dg₆₃的行需再次进行[3 1 2]的重排。原因在于输入矩阵与直传矩阵的列序feedin矢量（数组）由图1-3-48的⑥决定；而输出矩阵与直传矩阵的行序feedout矢量（数组）由图1-3-49的3决定。

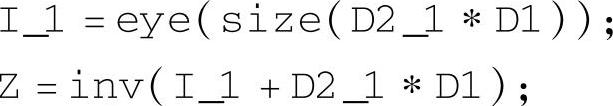
第4步：与第3步类似，将第1步重排后的B₁、D₁、C₁还原。

按上述4步将式（1-3-28）和式（1-3-29）推广后，将计算得到的反馈系统各系数矩阵与用feedback函数所得的对应矩阵进行比较，结果示于图1-3-52右下角的比较数组之中。二者结果一致。

需要注意的是，在上述推广方法中，式中计算出的系数矩阵（例如Bg₆₃等）行列还原（第3步）的排序方法与第2步的重排方法不总是相同的。它们之间构成一种特殊的“次序互补”变换。为进一步说明这种排序方法，再举例如下：设某矩阵A=[a₁a₂a₃a₄a₅]（a_n为其行或列），经过两次不同的行或列序重排还原，如图1-3-53所示。

图1-3-53 矩阵行列重排说明

第一次排序方法是[2 3 5 1 4]，而第二次排序的方法是[4 1 2 3 5]，两者是不同的。当然，也有两次排序的方法相同的情况。