1.状态空间对象和系数矩阵
如果已知系数矩阵A、B、C、D,可以使用基本函数ss构造状态空间对象。
命令

获得包含状态变量X、输入U、输出Y的连续状态空间对象模型。例如,给定所有系数矩阵A、B、C、D,运行上述命令可得以下结果:

如果已知状态空间的对象模型,可以使用命令dssdata
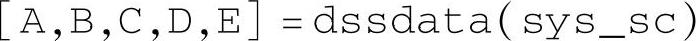
快速获取各系数矩阵及采样周期等“描述符”,其中矩阵E可以不输出。对于规范型状态模型,函数dssdata等价于函数ssdata,此时E=1(单位阵)。命令rmodel
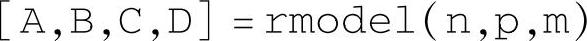
用于返回稳定的随机连续状态空间模型系数矩阵。
2.与传递函数及零极点模型的转换
存在两套平行的转换命令可以完成此功能。一套是状态空间对象模型转换成传递函数、零极点对象模型,分别使用命令tf,zpk
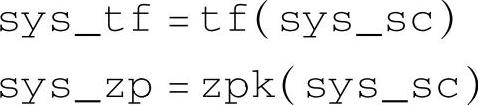
语句中的输入为状态空间对象模型sys_sc,输出分别是传递函数对象模型sys_tf和零极点增益对象模型sys_zp。如果输入是离散对象模型sys_sd,将获得对应的Z传递函数及其零极点增益。例如,当对上述状态空间对象模型sys_sc运行tf,zpk命令时,可以得到传递函数为(注意,本例的sys_sc是一个SISO系统)
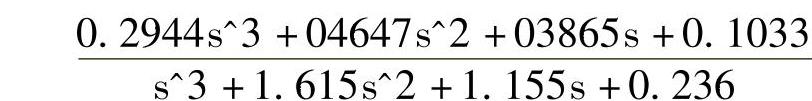
对应的零极点增益模型为
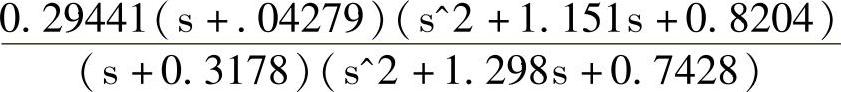
如果已知传递函数和零极点对象模型,可以使用命令ss转换成状态空间对象模型。另一套转换命令是“描述符”对“描述符”的相互转换。使用命令
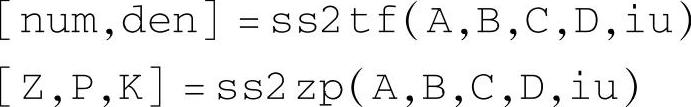 (https://www.xing528.com)
(https://www.xing528.com)
分别获得传递函数的多项式系数和零极点增益数值。其中,语句中的输入量iu表示实际状态空间模型中输入U的分量序号,就是式(1-3-4)中的序号j=1,2,…,m。使用命令
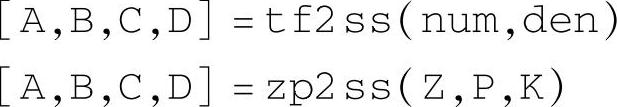
可以将传递函数或零极点增益模型还原成状态空间模型。对于MIMO系统,注意要将num、den、Z、P、K等全部列出。
前已述及,传递函数和零极点的相互转换命令为zp2 tf,tf2zp。将其推广到一般的MIMO系统时,传递函数分子多项式num的行数等于输出y的分量数p。与此对应,系统零点Z也不只一组,其组数也等于输出y的分量数p。同样,增益K也有p个。但是传递函数分母多项式den只有一行,极点P也只有一组。den是系统特征多项式系数,极点P是特征多项式的根,也是系统矩阵A的特征值。这些关系由式(1-3-2)描述。在MAT-LAB中式(1-3-2)写成
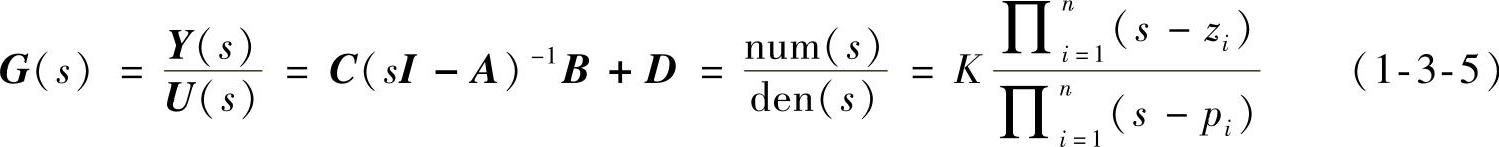
【例1-8】状态空间模型与传递函数、零极点增益模型转换仿真仪。
将一个随机生成的三阶状态空间模型转换成传递函数和零极点增益模型。程序如shili01_08所示。程序前面板图和框图面板如图1-3-2~图1-3-4所示。
程序说明:
由选择开关选择SISO和MIMO系统。当选择MIMO时,实例给出二输入、三输出系统。语句
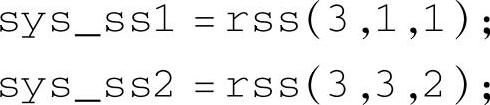
分别生成一个单输入、单输出和一个二输入、三输出的三阶状态空间对象模型,仿真仪自动进行传递函数和零极点转换。
由图1-3-2可见,对于SISO系统,输出矩阵C只有一行(p=1),输入矩阵B只有一列(m=1),传递函数分子多项式系数只有一行num11,与一行分母多项式系数den共同构成一个传递函数。与此相对应,零点只有一组Z11,增益只有一个K11。
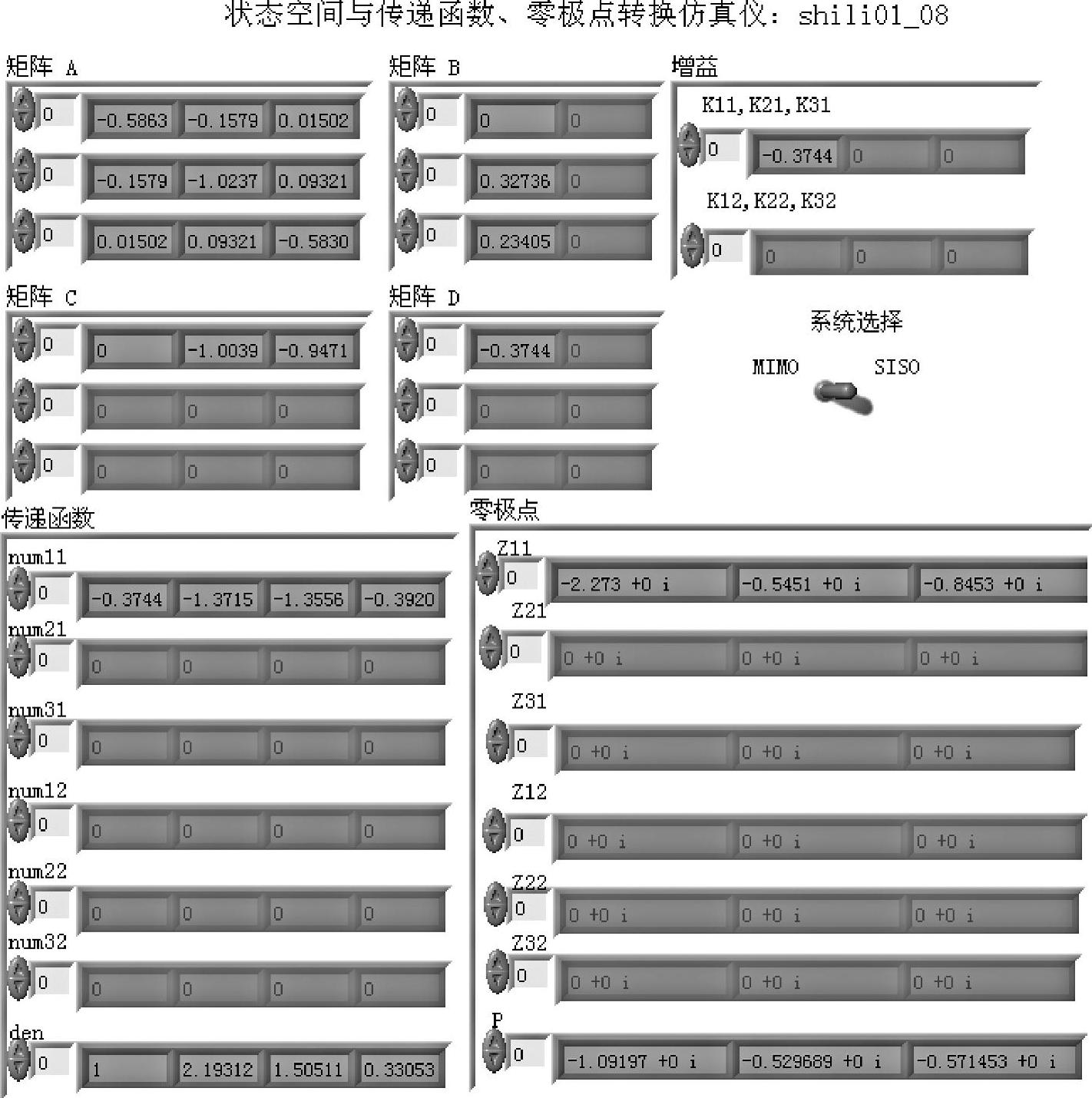
图1-3-2 程序shili01_08前面板(单输入、单输出)
对于图1-3-3所示的二输入、三输出状态空间模型,输出矩阵C有3行(p=3),输入矩阵B有2列(m=2),传递函数分子多项式系数有6行,与一行分母多项式den可以构成6个传递函数。与此相对应,零点有6组Z11~Z32,增益有6个K11。当然,与SISO系统相同,系统只有一组极点P。
仔细考查图1-3-3可以发现,实例的输出矩阵C中的第一行为全0。由式(1-3-5)可知,与num11和num12相对应的传递函数表达式前一部分为0,后一部分完全由矩阵D的第一行元素决定,应当为0或常数。num11为全0,对应传递函数为0。num12各项与den各项的公约数正是D(1,2)(使用num12./den计算,得[0.7936,0.7936,0.7936,0.7936])。从零极点看,Z12与极点P完全相同(使用[roots(den)′roots(num_12)′]计算,都得[-4.6642,-2.4263,-1.5288]),零极点对消后只剩下增益K21=D(1,2)。这说明,转换命令ss2tf、ss2zp并不给出最简结果。由于随机赋值,此例数值仅适用于图1-3-3,其框图面板如图1-3-4所示。
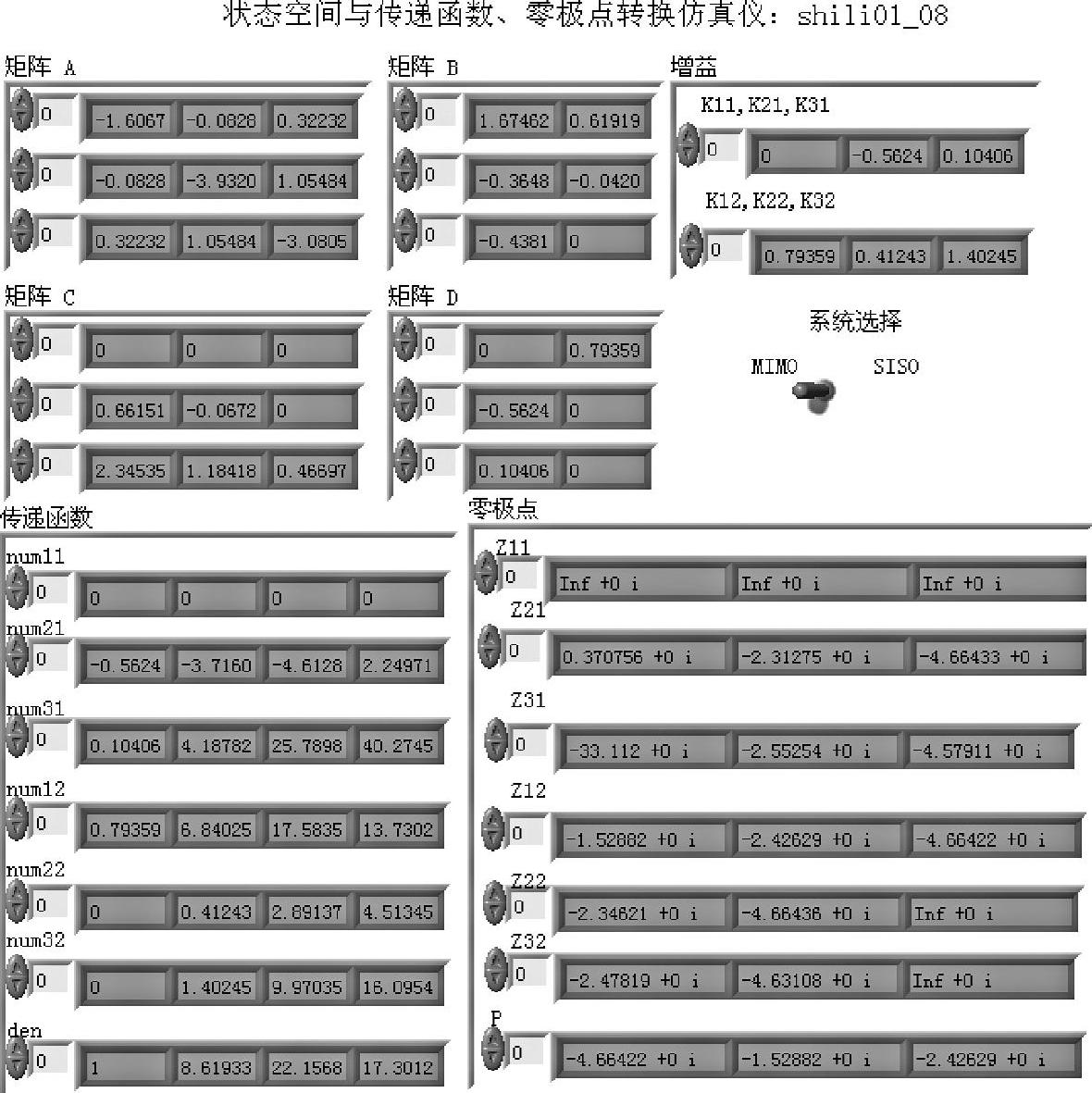
图1-3-3 程序shili01_08前面板(二输入、三输出)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




