传递函数框图的处理方法

用框图可以方便地表示传递函数的并联、串联及反馈。使用虚拟仪器功能，可以方便地获得框图变换结果。

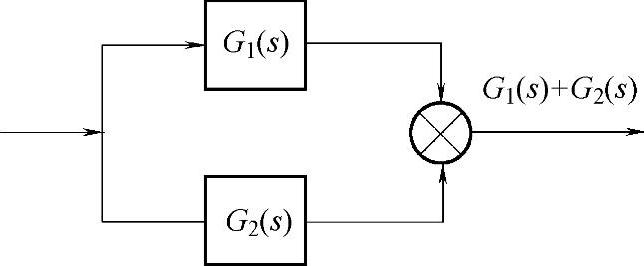
图1-1-3 传递函数的并联

1.并联

两传递函数的并联如图1-1-3所示。

两传递函数并联的等效传递函数为参与并联的传递函数的代数和。

基本语句如下：

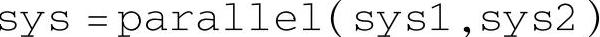
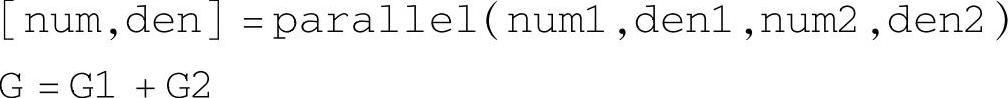
其中，第3条语句中的G₁和G₂最好使用上述的自变量d_s=zpk（′s′）语句书写。

【例1-2】设两传递函数G₁、G₂分别为

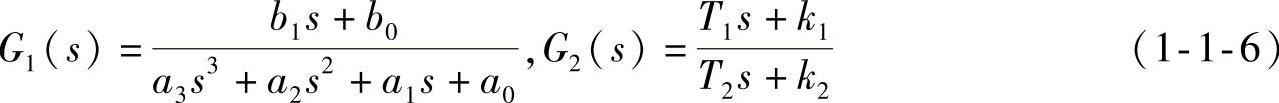
求并联等效传递函数。

设通过程序面板选定G₁的参数构成为式（1-1-4）。G₂中T₁=2，k₁=0；T₂=4，k₂=1，并联等效变换程序如shili01_02所示。程序shili01_02的框图面板和前面板分别如图1-1-4和图1-1-5所示。

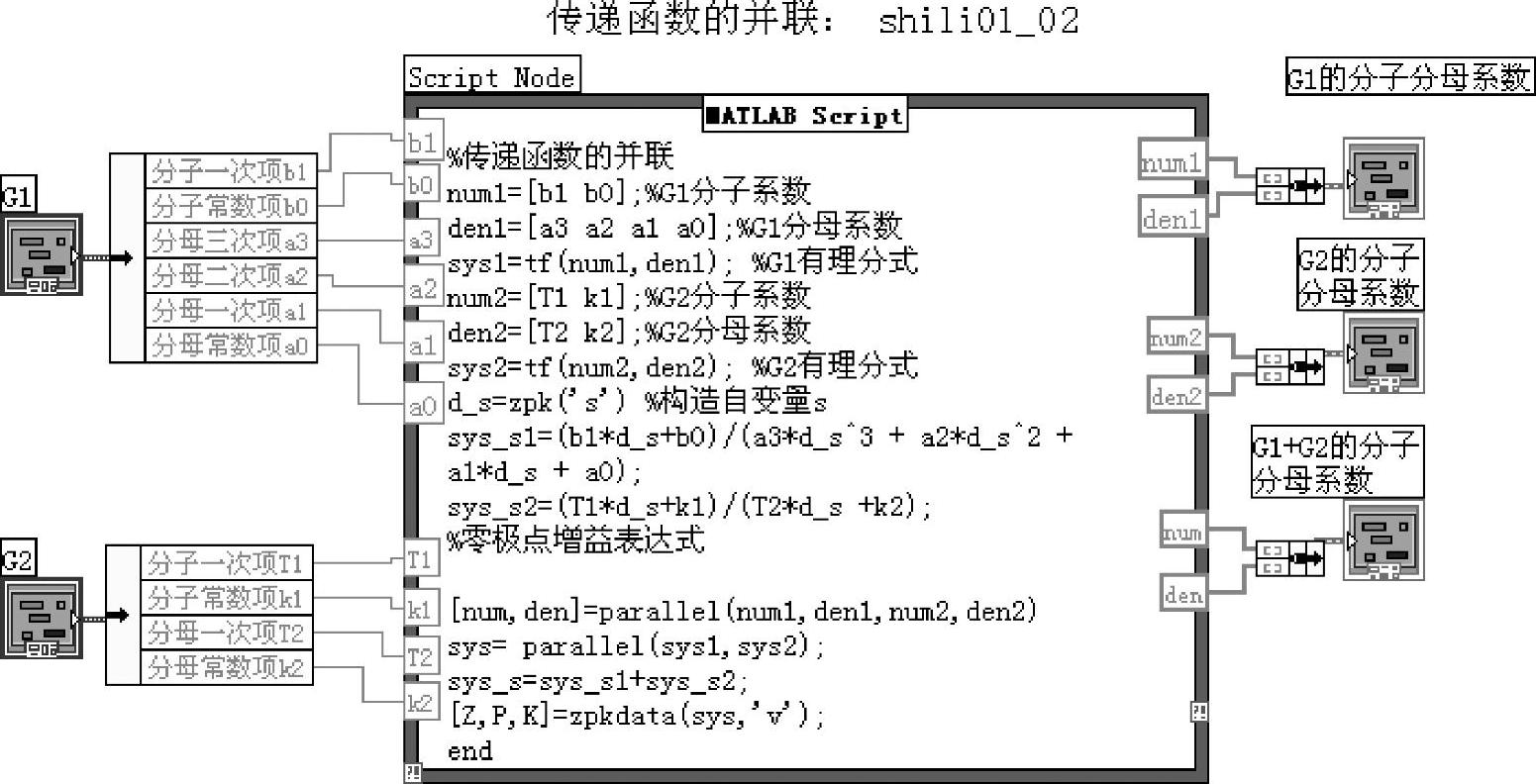
图1-1-4 程序shili01_02框图面板

在MATLAB命令窗口运行sys，得到G₁与G₂并联的多项式，见式（1-1-7）。

运行sys_s得到G₁与G₂并联的零极点增益形式，见式（1-1-8）。

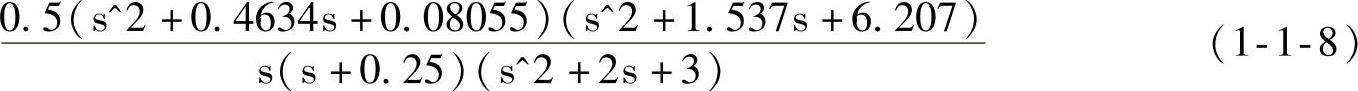
由式（1-1-8），再对比式（1-1-5）和式（1-1-6）可见，并联后传递函数的极点由参与并联的传递函数的极点共同组成。

注意：程序中实现并联功能的代数表达式语句为

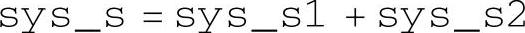
其中sys_s1与sys_s2都是用d_s形式书写的。

2.串联

两传递函数串联后的等效传递函数为参与串联的传递函数之积，如图1-1-6所示。

基本语句如下：

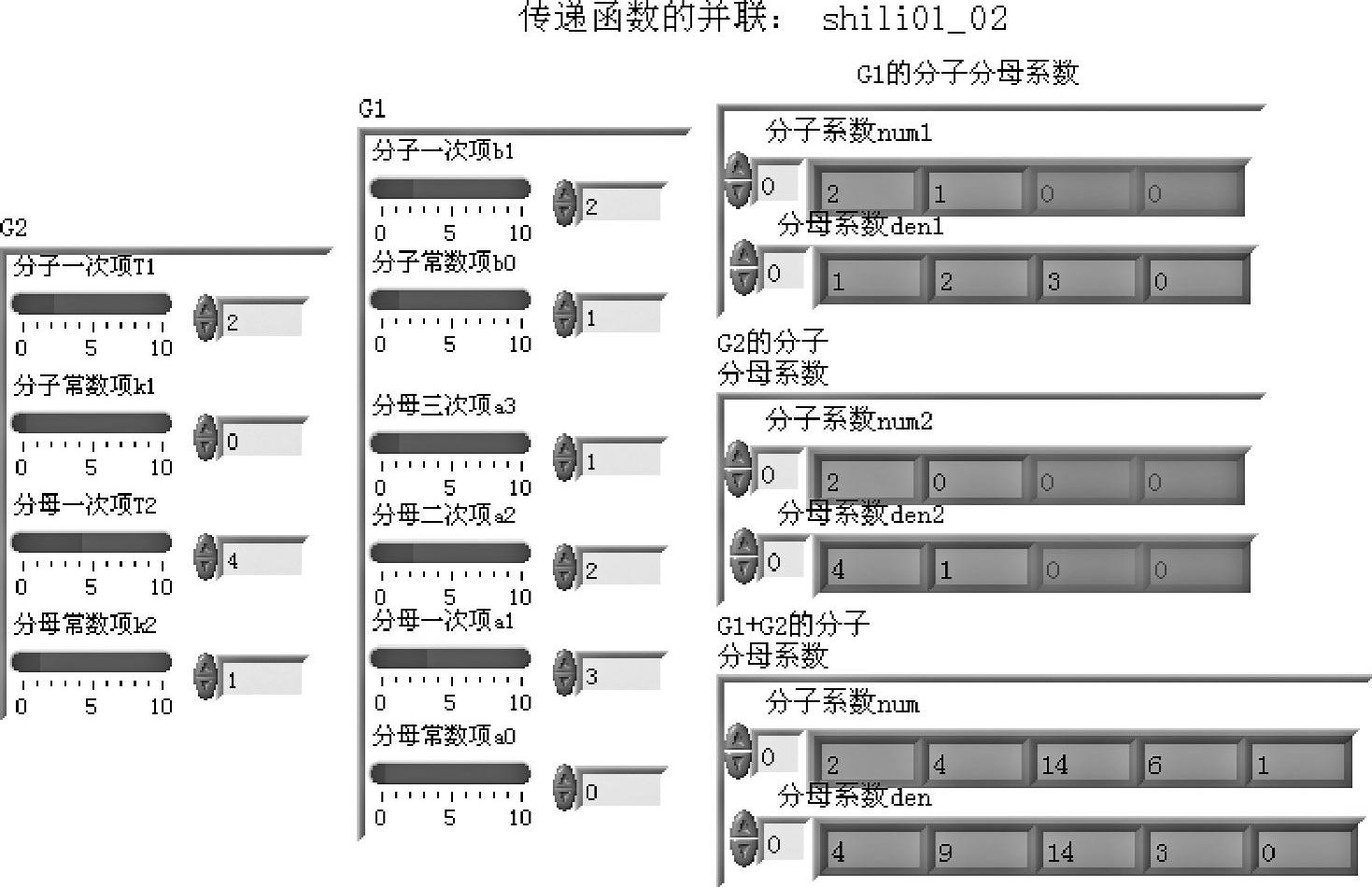
图1-1-5 程序shili01_02前面板

最后两条语句采用多项式乘法分别求取分子分母多项式的降幂系数。

【例1-3】设两传递函数G₁与G₂分别为

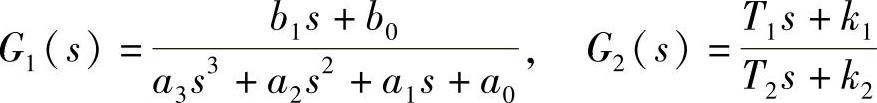
使用不同方法求其串联等效传递函数。

程序如shili01_03所示。通过程序面板选择与例1-2相同的参数，其框图面板和前面板分别如图1-1-7和图1-1-8所示。

在MATLAB命令窗口运行sys，得到G₁与G₂串联的多项式形式见式（1-1-9）。

图1-1-6 传递函数的串联

运行sys_s得到G₁与G₂串联的零极点增益形式见式（1-1-10）。

由式（1-1-10），再对比式（1-1-5）和式（1-1-6）可见，串联后传递函数的零极点分别由参与串联的传递函数的零极点共同组成，增益为各串联环节增益之积。

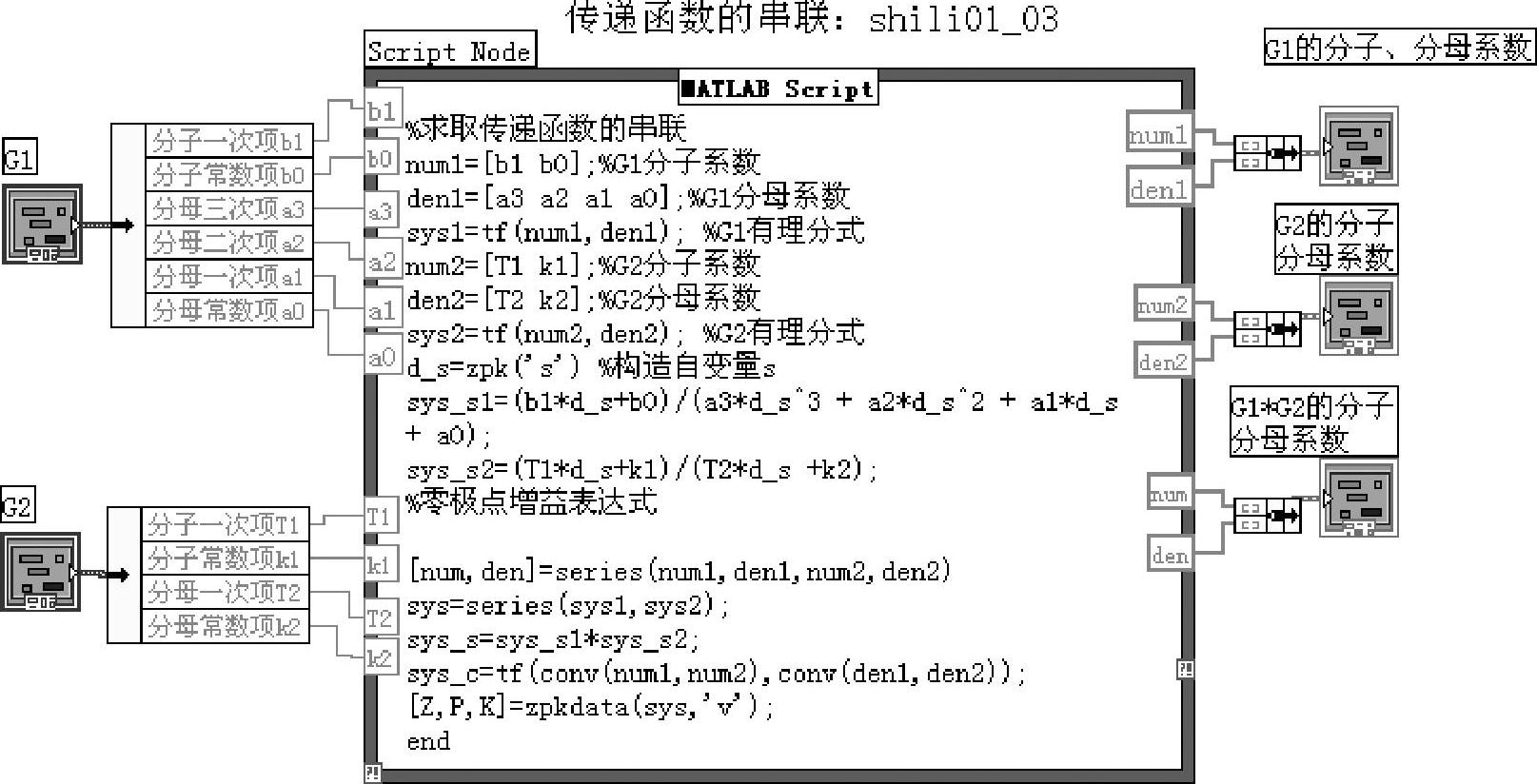
图1-1-7 程序shili01_03框图面板

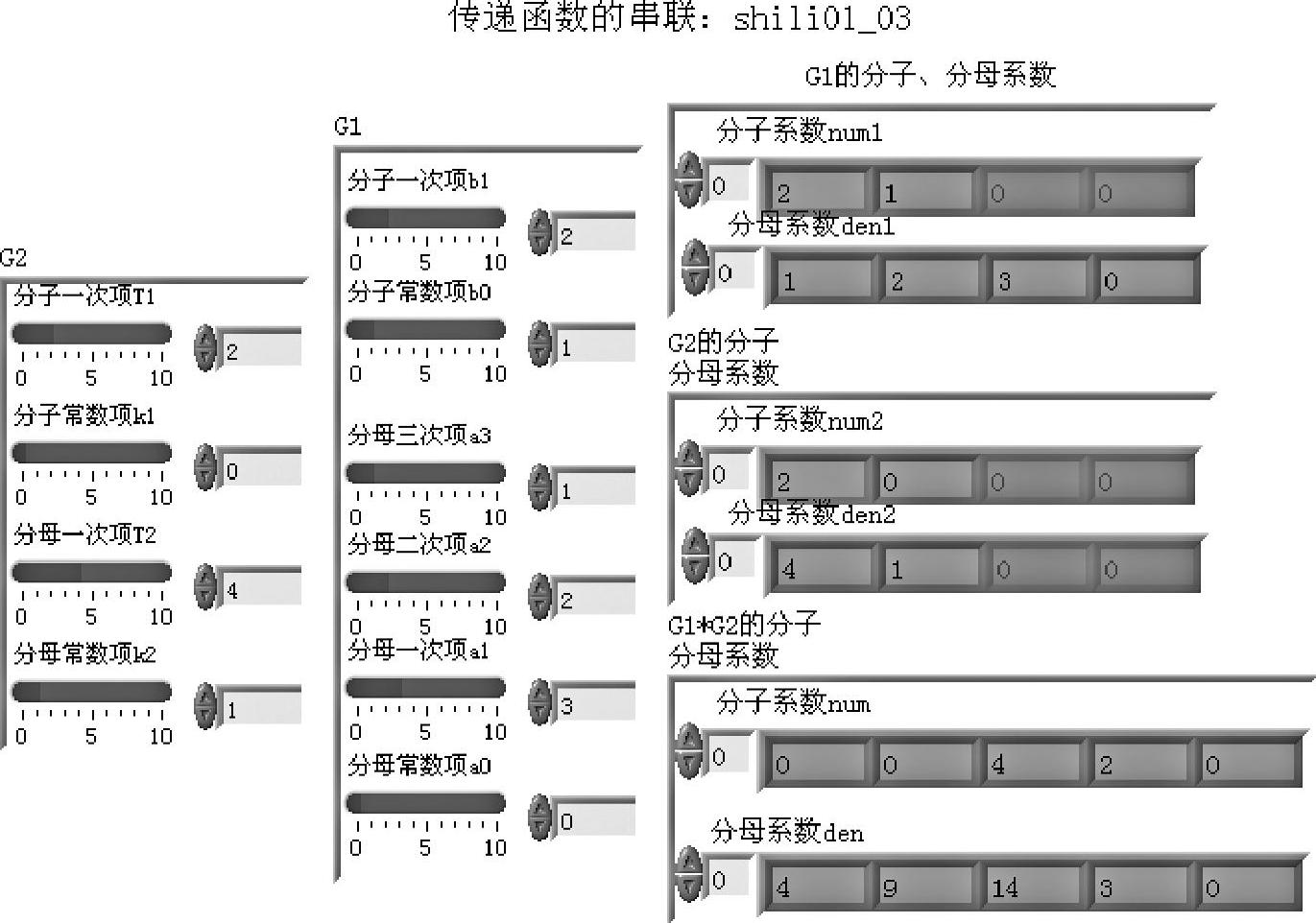
图1-1-8 程序shili01_03前面板

注意程序中

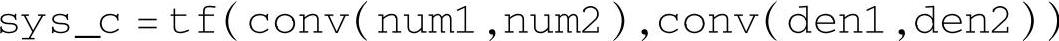
的构成方法。

3.反馈

有反馈时，等效传递函数为前向通道传递函数乘积与1加开环传递函数的比，如图1-1-9所示。

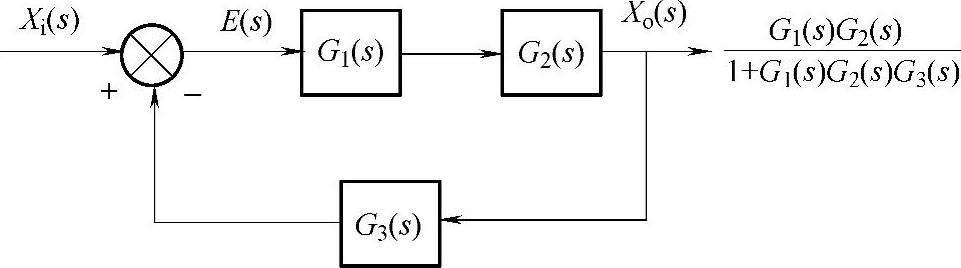
图1-1-9 传递函数的反馈连接(www.xing528.com)

基本语句如下：

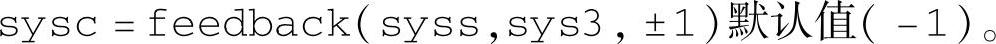
其中，syss为G₁与G₂的串联，表示前向通道传递函数。

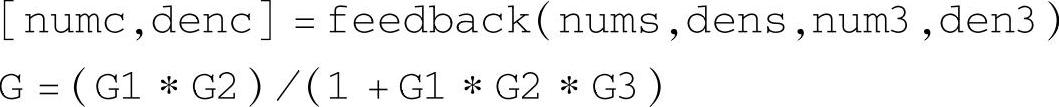
其中，最后一条语句采用代数式书写方式，式中的G₁、G₂、G₃是用自变量s定义的。

【例1-4】传递函数G₁与G₂分别为

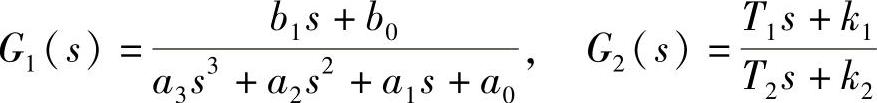
设（1）G₁与G₂串联构成前向通道传递函数，比例反馈系数为k。

（2）前向通道传递函数为G₁，反馈传递函数为G₂。

求取以上两种情况下的负反馈等效闭环传递函数。

程序如shili01_04所示。通过程序面板选择与例1-3相同的参数，其框图面板和前面板分别如图1-1-10和图1-1-11所示。

图1-1-10 程序shili01_04框图面板

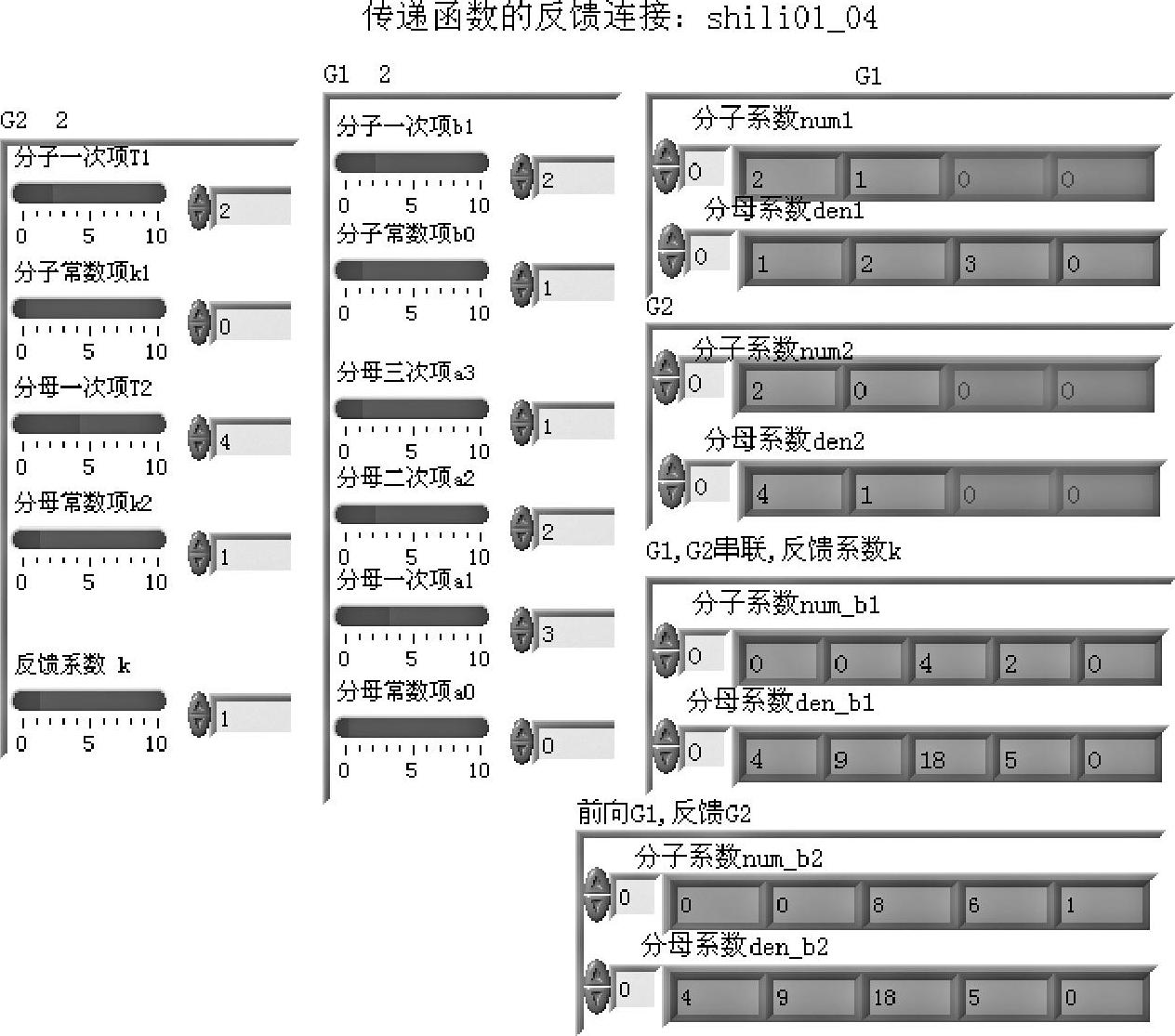
图1-1-11 程序shili01_04前面板

在MATLAB命令窗口运行sys_b1，得到例1-4中（1）的闭环传递函数，见式（1-1-11）。

运行sys_b2得到例1-4中（2）的闭环传递函数，见式（1-1-12）。

对比式（1-1-11）和式（1-1-12）可见，当k=1，即情况（1）为单位负反馈时，例1-4中（1）、（2）两种情况有相同的闭环极点。

注意程序中的语句

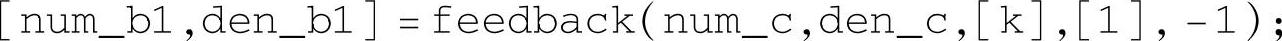
的构成方法。

【例1-5】化简图1-1-12，求出系统等效传递函数。

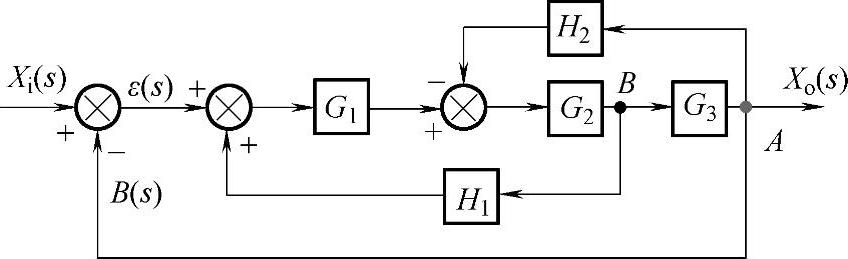
图1-1-12 框图化简实例

按照框图化简规则，容易得到系统等效传递函数。给定图中各传递函数的具体形式和参数，通过虚拟仪器仿真，可以方便地获得等效传递函数的有理分式及零极点增益模型。程序如shili01_05所示。程序框图面板和前面板分别如图1-1-13和图1-1-14所示。

图1-1-13 程序shili01_05框图面板

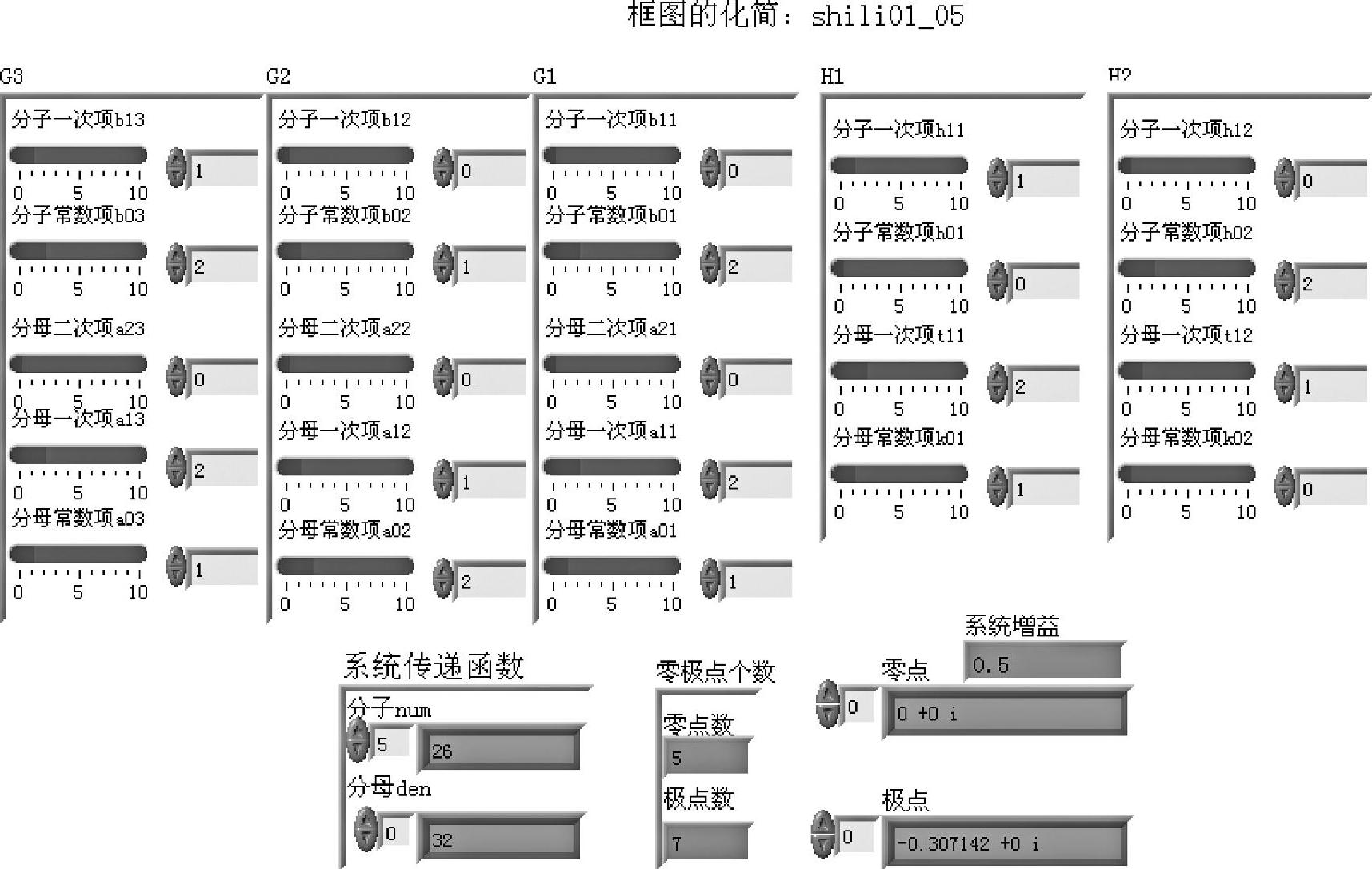
图1-1-14 程序shili01_05前面板

程序说明：

为简洁起见，例1-5中设定前向通道传递函数G₁、G₂、G₃由一个导前环节和一个二阶环节构成，即

反馈通道传递函数H₁、H₂由一个导前环节和一个惯性环节构成，即

通过程序面板选择待定系数，特别是选择某些系数为0时，可以获得多种环节组合。例如按照图1-1-12所示的各个环节，在前面板上选择各实际仿真传递函数

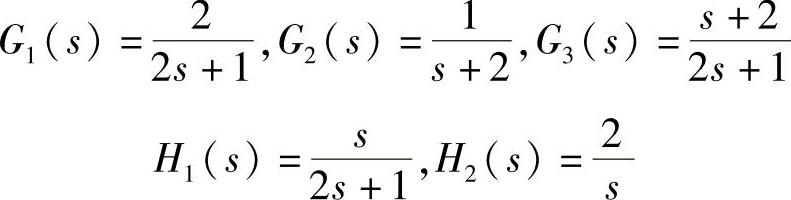
则系统闭环传递函数（sys_bh）为

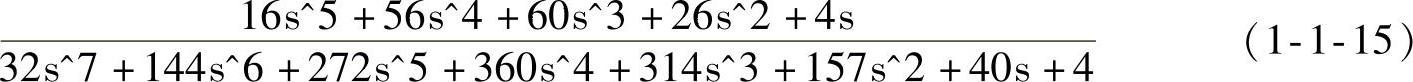
根据框图化简规则，获得的闭环传递函数表达式为

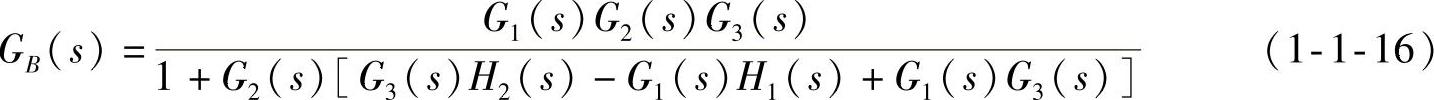
可以验证，若将各仿真传递函数带入式（1-1-16），可得式（1-1-15）。程序中使用语句

运算式（1-1-16），得到一个未约简的表达式，约简之后与式（1-1-15）相同。式（1-1-15）表明，该系统有5个零点，7个极点。

在MATLAB窗口运行sys_zp语句，可以获得系统的零极点增益形式为

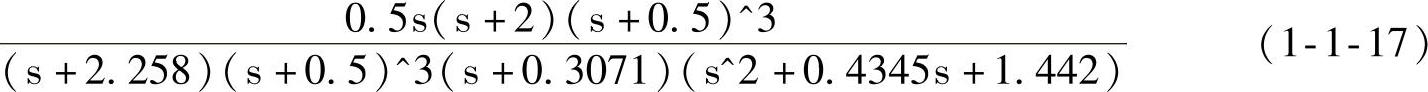
实际上，由式（1-1-17）可见，系统闭环传递函数式（1-1-15）也非最简约形式，还可以进行零极点对消，以获得最简约形式，即

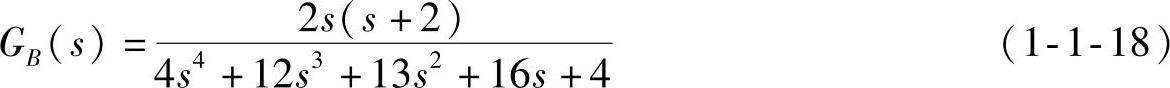
后面进行时域特性分析时可以证明，式（1-1-15）、式（1-1-17）和式（1-1-18）3个表达式的动态特性和稳态特性都相同。由式（1-1-17）可以直接判断系统是稳定的，还可以使用谢绪凯—聂义勇^[5]判据判断式（1-1-15）和式（1-1-18）的稳定性。

程序前面板在显示式（1-1-15）的多项式系数和零极点数值时，使用了数组索引方式。改变索引值，可以获得对应项的数值。需要注意的是，LabVIEW中的数组索引是从0开始编号的。