逆运动学分析方法探究

Manipulator Algorithms子模块库中包含Inverse Kinematics模块，可用于机械臂机器人逆运动学的求解，如图7.42所示。

该模块接受一个4×4的末端执行器位姿的齐次变换矩阵输入、一个1×6的末端执行器的方向和位置公差的权重向量输入，以及一个初步预测的关节转角行向量输入，输出为计算得到的N×1的关节转角列向量。同样地，该模块也需要一个自定义的机器人刚体树实例对象作为模块模型参数的输入，可参考7.4.1节所述，通过各关节的几何和物理参数构建各关节的实体Body，然后连接起来得到串联的刚体树模型。

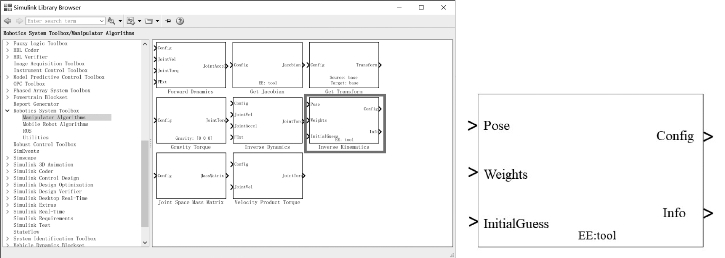
图7.42　Inverse Kinematics模块

对于Staubli TX200机器人，构建其逆运动学求解的Simulink模型，如图7.43所示。

图7.43　用于逆运动学求解的Simulink模型

定义各关节的求解精度权重矢量为［1 1 1 1 1 1］，模块模型参数输入的刚体树实例对象为7.4.1节中已经定义的treerbt对象，InitialGuess和Info参数暂不设置，Pose输入即末端执行器的齐次变换矩阵分别为：

(www.xing528.com)

计算得到的关节向量q分别记为：

output_q1＝［0 0 0 0 0 0］

output_q2＝［3.141 6，2.787 3，3.141 6，-2.266 9，2.434 7，1.342 3］

对比发现，T＝Tz时两种方法求解结果output_q1和qz基本一致，但T＝Tn时对应各关节坐标的求解值output_q2和qn＝［0，-1.570 8，-2.356 2，0.785 4，0.785 4，0］却不同。若采用前述的机器人工具箱根据关节坐标计算正运动学末端执行器位姿矩阵，输入output_q2＝［3.141 6，2.787 3，3.141 6，-2.266 9，2.434 7，1.342 3］，计算可得：

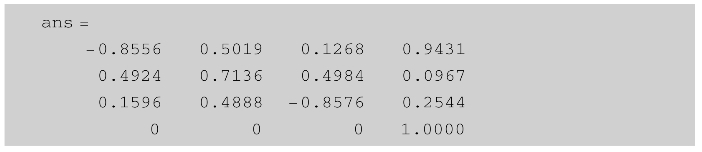
经对比发现，在一定精度下这两个不同的关节坐标对应的末端执行器位姿矩阵基本一致，这也证明关节坐标位置解output_q2和qn是同一末端执行器位姿对应的两种不同的位形解。若给定一个初步预测的关节位置坐标向量解prd_qn作为InitialGuess节点的输入，例如给定prd_qn＝［0 0-1-2 0 0 0］，添加prd_qn输入建立新的Simulink模型，如图7.44所示。

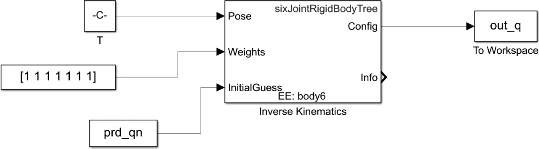
图7.44　包含InitialGuess输入的逆运动学求解模型

此时求得的out_q＝［0.000 0，-1.570 8，-2.356 2，0.785 4，0.785 4，-0.000 0］，与qn关节坐标一致，InitialGuess接口可以根据输入的预测值计算与之相近的位形解，从而选择想要的位形解。