正动力学分析的重要性与方法

机器人的正动力学分析是在已知各关节驱动力矩和力时求解得到机器人的运动参数，包括关节广义位移、关节速度和关节加速度。在实际应用中，主要通过正动力学分析来对机器人的运动进行仿真。要根据施加的关节力和力矩确定机械臂的运动。由方程式（6-23）可以得到关节的加速度为：

机器人工具箱中的fdyn和accel函数可用于机器人正动力学相关计算。其中，fdyn函数用于计算各关节的角度和角速度；accel函数主要用于计算关节的角加速度。

fdyn函数可在输入关节所受到的力矩时，计算出仿真过程中每个采样时刻对应的各关节的角度、角速度（均为国际单位制）。其调用格式如下：

其中，t为仿真的时长，输入参数torqfun为自定义施加的关节力矩函数，返回时间间隔向量T、各关节的转角q和各关节的角速度qd。默认初始的转角q0和角速度qd0都为0。除此之外，还可以为此函数添加额外的参数输入，包括自定义关节的初始转角和角速度q0，qd0，以及自定义的关节力矩控制参数ARG1，ARG2等。例如，如果选择PD控制器去控制关节力矩，可以定义如下的关节力矩函数mytorqfun.m。

以前述的Staubli TX200机器人为例，定义仿真时长为t＝10×10-4 s，给定P＝10，D＝10，在命令交互行中输入：

可以求得0～t时间间隔内各个位形瞬时机器人各个关节的转角q和角速度qd，分别如图6.19和图6.20所示。

根据式（6-26）可以推导出机器人的关节加速度，并可以使用机器人工具箱中的accel函数进行正动力学的计算。accel函数用于在给定各关节转角和角速度下求解机器人各关节的角加速度qdd，调用形式如下：(www.xing528.com)

其中，参数q和qd分别为各关节的转角和角速度1×N行向量；torque为各关节所受外力矩1×N行向量，该函数返回各关节的加速度计算值N×1列向量，其中N为关节数。当q，qd和torque为M×N矩阵时，求得的qdd为M×N的矩阵且各行表示不同位姿和关节角速度对应的各关节的角加速度计算值。

对于Staubli TX200机器人，若给定一般位形qn＝［0-pi／2-3∗pi／4 pi／4 pi／4 0］处机器人的各关节的角速度为qd＝q1＝［1　1　1　1　1　1］，单位为rad／s，给每个关节处施加转矩为torque＝［10　10　0　10　0　10］，单位为N，计算各关节的角加速度如下：

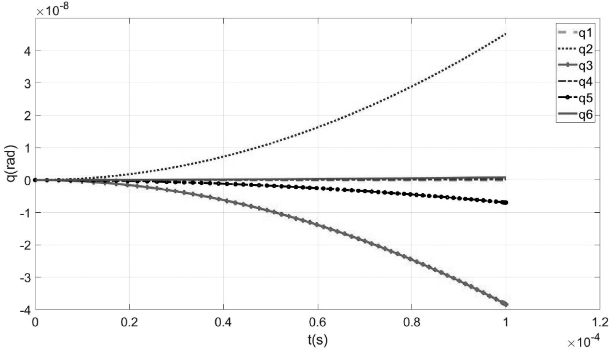
图6.19　在0～t时间间隔内各位形瞬时机器人各关节的转角

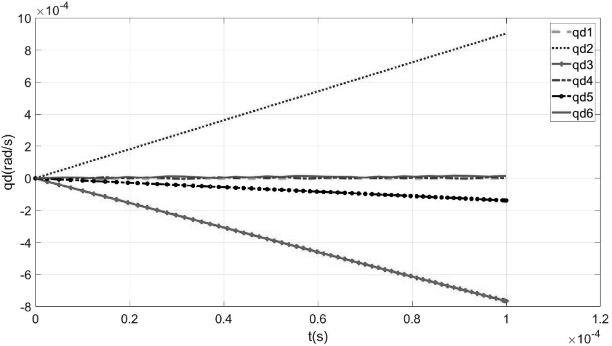
图6.20　在0～t时间间隔内各位形瞬时机器人各关节的角速度

单位为rad／s2。

综上可知，使用机器人工具箱进行机器人正动力学计算时，首先可通过调用机器人工具箱中的fdyn函数，在已知机器人初始关节转角、关节角速度和各关节给定作用力矩下，求出在一定时间间隔后各关节的转角和角速度。然后调用accel函数，并将fdyn函数求解得到的所有时刻机器人各关节转角、速度和受到的作用力矩作为accel函数的输入，从而求解出每个位形对应的机器人各关节的角加速度，这样就在已知各关节驱动力矩和力时求解得到机器人的运动参数，完成了机器人正动力学的计算。在实际应用中，往往使用这一正动力学计算过程来进行机器人的动力学仿真，研究其在给定作用力和力矩下是否按照预想的轨迹和运动学参数进行运动。