动力学方程解析

对于多关节机械臂机器人系统，要进行整个系统的动力学描述，需要对单个关节的动力学特性进行分析。多关节机械臂机器人的单个关节除了受到电动机的转矩作用外，还受到相邻连杆的重力产生的力矩作用，以及相互旋转中的连杆所施加的陀螺力产生的力矩作用和惯性力矩作用等。

如图6.17所示，分析关节i处受力可知，关节i处的电动机对连杆i施加转动力矩作用的同时，受到连杆i-1的反作用力矩，关节i处受到电动机的驱动力矩Mm，还受到关节i-1因相对关节i转动而产生的陀螺力矩M0的作用，以及惯性力矩和等的作用。单个连杆的受力情况复杂，难以描述其动力学方程，通常对于一系列的连杆，其动力学特性可以用多刚体系统的动力学公式描述，可由一组简洁的矩阵形式的耦合微分方程表示为：

其中，q，，分别为广义的关节位置、关节速度和关节加速度；M为关节的空间惯量矩阵；C为科氏力和向心力耦合矩阵；F为摩擦力；N为重力；τ为与广义坐标q对应的广义驱动力向量。最后一项描述施加在末端执行器处的外力f在各关节处产生的关节力，其中，J为雅可比矩阵。矩阵M，C，F，N是连杆的运动学D-H参数（θi，di，ai-1，αi-1）和惯性参数的函数，每个连杆i在以其质心为原点且与关节坐标系｛i｝平行的坐标系中具有以下物理参数：连杆质量m、相对于连杆坐标系的质心r和转

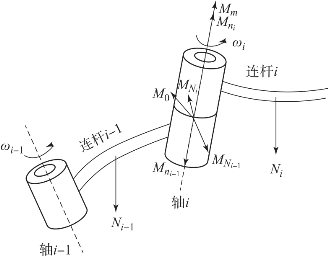
图6.17　多关节机器人相邻连杆间关节的受力情况

动惯量I。其中转动惯量I为包含六个独立元素的二阶矩阵：

式中，主对角线元素为惯性矩，非主对角线元素为惯性积。9个元素中只有6个是独立的，可表示如下：

在机器人工具箱环境下，连杆的运动学参数和惯性参数可以使用Link对象或者SerialLink对象中的dyn函数进行查看，也可以直接打开Link实例变量进行属性查看和修改。前例Staubli TX200机器人部分关节的动力学参数如下：

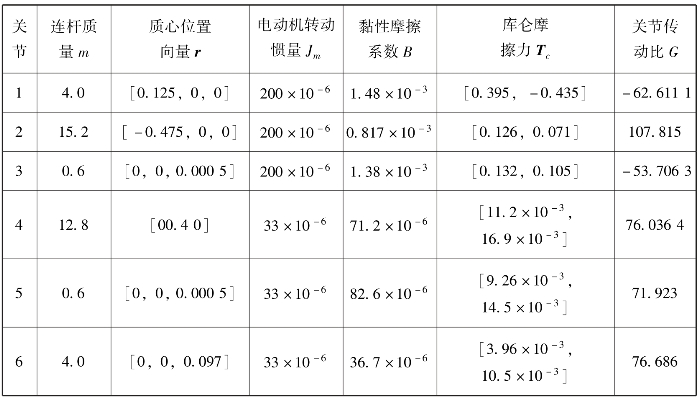
其中，B，Tc和G分别为电动机的黏性摩擦系数、库仑摩擦力和关节传动比。m，r，I，Jm则分别为连杆质量、质心位置、连杆惯量矩阵和电动机转动惯量。

为了便于计算，将Staubli TX200机器人的标准D-H参数单位统一为m，并重新构建SerialLink机器人对象。给定各关节的物理参数见表6.6。

表6.6　Staubli TX200连杆机器人关节和关节电动机的物理参数

连杆惯量矩阵分别为：

L1：I1＝［0.3200 0.2433 0.2433 0 0 0］　L2：I2＝［1.2160 1.8113 1.8113 0 0 0］

L3：I3＝［0.0241 0.0241 0.0480 0 0 0］L4：I4＝［1.3653 1.0240 1.3653 0 0 0］

L5：I5＝［0.0241 0.0241 0.0480 0 0 0］L6：I6＝［0.2247 0.2247 0.3200 0 0 0］

下面介绍在MATLAB中如何使用工具箱计算得到机械臂机器人不同姿态时的M（空间惯量矩阵）、C（科氏力和向心力耦合矩阵）、F（摩擦力矩阵）和N（重力矩阵）。

（1）空间惯量矩阵M（q）

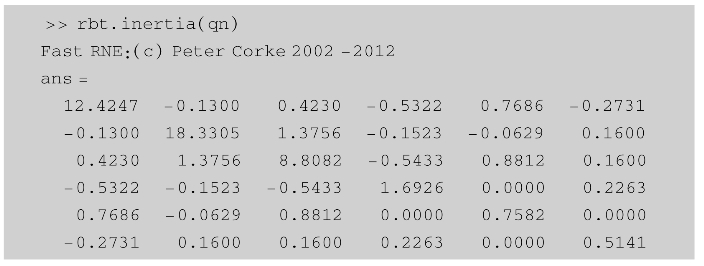
机器人关节的空间惯量矩阵是机械臂各关节的位姿的函数，在不同的机器人位形时具有不同的值。在机器人工具箱中，可以使用SerialLink类的inertia方法来计算不同位形的关节空间惯量矩阵。该函数调用形式如下：

其中，q为各关节转角组成的1×N行向量，返回N×N空间惯量矩阵。关节转角输入也可以写成K×N矩阵的形式，此时返回值为N×N×K的三维矩阵，表示K个位形时分别对应的空间惯量矩阵。

对于Staubli TX200机器人，可计算其在一般位形关节坐标qn＝［0-pi／2-3∗pi／4 pi／4 pi／4 0］时的关节空间惯量矩阵M（q）如下：

（2）科氏力和向心力耦合矩阵C（q，q·）

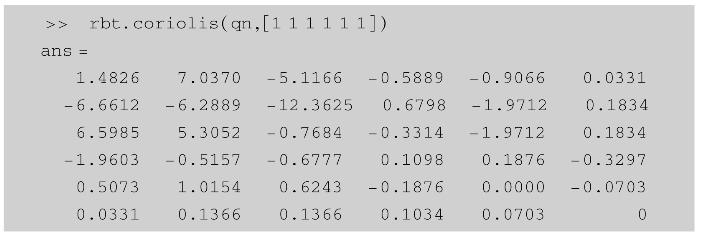
科氏矩阵C是关节坐标和关节速度的函数，是科氏力和向心力的耦合矩阵，表现为正定矩阵。在机器人工具箱中，可使用SerialLink类的coriolis方法来计算给定关节坐标和关节速度的科氏矩阵。coriolis函数的调用形式如下：(www.xing528.com)

其中，q，qd为由各关节的关节转角和角速度组成的1×N行向量，返回N×N科氏矩阵。关节转角和角速度输入也可以写成K×N矩阵的形式，此时返回值为N×N×K的三维矩阵，表示K个位形时分别对应的科氏矩阵。

在前例中，如果给定在一般位形qn＝［0-pi／2-3∗pi／4 pi／4 pi／4 0］处各关节的关节角速度为qd＝［1 1 1 1 1 1］（单位为rad／s），则相应的科氏矩阵为：

（3）重力矩阵N（q）

重力矩阵与机器人的位形q有关，是对各关节所受重力的描述，且其值不受机器人的运动的影响。在实际应用中，往往通过一定的方法如外加弹簧等来抵消部分重力的影响。

在前例Staubli TX200中，对于一般位形qn＝［0-pi／2-3∗pi／4 pi／4 pi／4 0］处，可使用工具箱中SerialLink对象的gravload函数求解，该函数调用形式如下：

其中，q为由各关节的关节转角组成的1×N行向量，返回1×N重力矩阵。关节转角输入也可以写成K×N矩阵的形式，此时返回值为1×N×K的三维矩阵，表示K个位形时分别对应的重力矩阵。grav为附加的参数，表示自定义重力加速度向量。

计算qn位形处重力矩阵N：

由于输入为标准单位制，故函数输出各关节所受重力大小的单位为N。

（4）摩擦力矩阵F（）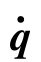

摩擦力矩阵F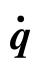（）是由各关节的给定摩擦力参数值决定的，大小与各关节的转速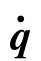有关。机器人各关节处会受到摩擦力的作用，通常在关节还未转动前主要受到静摩擦力的作用。一旦关节转动起来，则主要受到黏性摩擦力的作用，且黏性摩擦力的大小与黏性摩擦系数成线性关系，可以用图6.18进行描述。

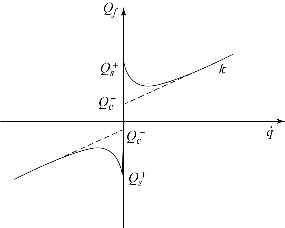
图6.18　摩擦力相对于速度的特性

图6.18中，斜率k表示黏性摩擦系数，Qs表示静摩擦力，Qc表示库仑摩擦力，电动机摩擦力的正负取值取决于电动机的转动方向。通常来说，黏性摩擦系数的值是一定的，与电动机的转动方向无关，并可通过电动机厂商的数据手册得到。但库仑摩擦力的大小却与方向有关，对于某个连杆对象而言可正可负。利用机器人工具箱中的SerialLink类的friction方法可以快速求解出在给定各关节转速qd时各关节受到的摩擦力的大小。其调用形式如下：

其中，qd为由各关节的角速度组成的1×N行向量，返回1×N摩擦力矩阵。关节角速度输入也可以写成K×N的形式，此时返回值为N×N×K的三维矩阵，表示K个位形时分别对应的摩擦力矩阵。

对于Staubli TX200机器人的L1关节，根据实际值给定如下关节参数。黏性摩擦系数B和库仑摩擦力Tc的值如下：

并给定各关节的传动比G＝［-62.611 1，107.815，-53.706 3，76.036 4，71.923，76.686］：

对于一般位形qn＝［0-pi／2-3∗pi／4 pi／4 pi／4 0］处，利用工具箱计算各关节摩擦力：

单位为N。另外，可以使用工具箱里SerialLink类的jacob函数和jacobn函数分别求解世界坐标系下和末端操作器空间下的雅可比矩阵J（q）T。这样利用MATLAB的工具箱就可以在已知机器人位形和各关节角速度时确定方程（6-23）的系数矩阵。但是对于包含多个瞬时位形的某个运动过程来说，方程（6-23）的求解仍然很困难。

对于方程（6-23）的求解，目前主要有牛顿-欧拉法、拉格朗日法、空间矢量法和凯恩法等。其中牛顿-欧拉法是利用牛顿定律和欧拉方程建立动力学模型的方法，其主要思路是对机器人每个连杆质心的移动和转动分别应用牛顿定律和欧拉方程。首先由基座开始，从1号杆到末端执行器所在N号杆递推，求出各杆的速度和加速度。再从N号杆向1号杆进行递推，计算各杆受到的作用力和力矩，以及各关节的驱动力矩。相比其他方法，其具有更明确的迭代方程形式和更高效的迭代效率，因而很适合计算机求解。在机器人工具箱中，通常使用SerialLink类中的基于牛顿-欧拉法的fdyn，accel和rne函数对方程（6-23）分别进行正动力学和逆动力学的求解。