机械臂五次多项式轨迹规划详解

欲使机械臂末端执行器由初始位姿变化到目标位姿，由于机械臂末端执行器位姿对应的关节向量可由逆运动学求得，可求出末端执行器初始位姿和目标位姿分别对应各个关节的转角，因而只需要求得各个关节角随时间的变化函数即可进行机器人运动的轨迹规划。设机械臂末端执行器在t0时刻为初始位姿，在tf时刻为目标位姿，并设某个关节在t0时刻转角为θ0，在tf时刻转角为θf，可采用多种光滑函数θ（t）对该关节的转角变化进行插值，如图6.15所示。

要获得一条平滑的曲线，显然要对θ（t）施加四个约束条件：

图6.15　某一关节的几种可能路径

式中，前两个约束条件确定了初始值和最终值，后两个约束条件则保证了关节速度函数的连续。

次数至少为三的多项式才能满足这四个约束条件。一个三次多项式有四个参数，可以证明上述四个约束条件可唯一确定一个三次多项式，该三次多项式形式如下所示。

约束条件为：

上述方程组的解为：

可以看出该方法仅适用于关节起始角速度和终止角速度都为零的情况。

当要确定路径段起始点和目标点的位置、速度和加速度时，使用三次多项式往往无法满足要求，此时可以采用更高阶的五次多项式进行插值。记某个子过程机器人的某个关节的运动轨迹函数为：

速度和加速度方程分别为：(www.xing528.com)

定义初始时刻t0的位置为起点值θ0，结束时刻tf的位置为终点值θf，若已知初始时刻t0和结束时刻tf时该关节的关节角速度分别为和，关节角加速度分别为和，解上述方程组可以得到多项式中的各未知系数。

上述线性方程组的解为：

机器人工具箱中提供了tploy，lspb，jtraj和ctraj等函数，可用于轨迹规划。其中tploy为五次多项式曲线进行关节转角变化的拟合，得到的轨迹函数为一阶导数、二阶导数都是连续光滑的多项式曲线。但由于高次多项式轨迹曲线的计算量较大，故常采用直线段来构造简单的轨迹曲线。仅考虑在不同直线段的交接处会发生速度跳变（位移曲线不光滑）的情况，用抛物线在交接处进行拼接就可以得到光滑的轨迹，lspb函数即是采用这种方法，用梯形速度曲线（trapezoidal velocity trajectory）进行各关节转角变化的拟合。这里重点介绍常用于轨迹规划的jtraj和ctraj函数。

jtraj函数用于在关节空间下机器人两个不同位形间各关节角度变化插值拟合生成轨迹，ctraj函数用于在笛卡尔空间下机器人两个不同位形间末端执行器位姿变化插值拟合生成轨迹，调用格式分别如下。

［q，qd，qdd］＝jtraj（q0，qf，m）：其中，q0为初始关节角度；qf为终止关节角度；m表示过程包含的时间步数，每个时间步对应一个瞬时位形。该函数利用五次多项式进行插值规划轨迹，默认初始和终止时关节速度和加速度的值均为零。

tc＝ctraj（T0，T1，n）：其中，T0为初始末端执行器位姿矩阵；T1为终止时末端执行器位姿矩阵；n为路径中插值点的个数。该函数利用匀加速、匀减速运动规划轨迹，同样默认初始和终止时关节速度和加速度的值均为零。

【例6.6】　对例6.4中生成的机械臂通过五次多项式插值进行轨迹规划，使其由关节角为［0 0 0 0 0 0］的位姿运动至关节角为［pi／4-pi／3 pi／5 pi／2-pi／4 pi／6］的位姿。

程序如下：

程序运行结果如图6.16所示。

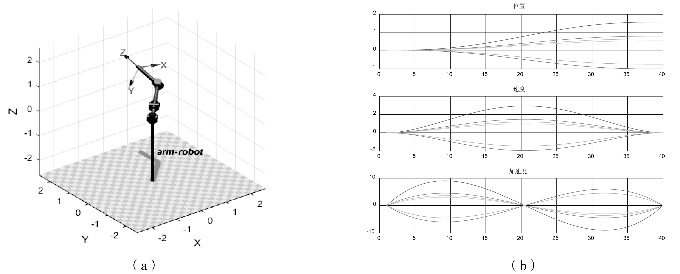
图6.16　五次多项式插值轨迹规划

（a）三维模型；（b）路径点位形处的关节位置、速度和加速度