刚体姿态描述及坐标变换方法

1.位置描述

描述一个刚体的位置，首先需要建立一个坐标系，即确定是在哪个坐标系下描述刚体的位置。刚体在某一瞬时的位置是唯一的，但在不同坐标系下的描述却不尽相同。本书主要通过建立笛卡尔坐标系对刚体的位置进行描述。

如图6.2所示，建立坐标系｛A｝，则刚体上任意一点都可以由一个3×1的位置向量AP来表示。

2.姿态描述

除了描述刚体的位置外，还经常需要描述其姿态。为了描述物体的姿态，将一个坐标系固定在刚体上，并给出此坐标系相对于参考坐标系的描述。在图6.3中，坐标系｛B｝是与刚体固连的坐标系，这样｛B｝相对于｛A｝的描述就足以表示出物体的姿态。

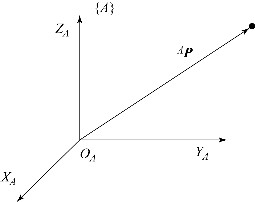
图6.2　物体位置描述

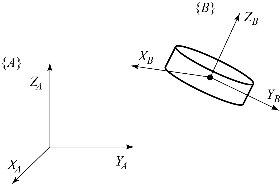
图6.3　物体姿态描述

用（XB，YB，ZB）表示坐标系｛B｝的主轴方向，它们在坐标系｛A｝中的描述如下：

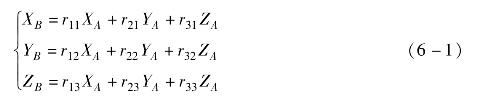
由这些系数构成的矩阵就是坐标系｛B｝相对于坐标系｛A｝的描述，称为旋转矩阵，用ABR表示。由于标量rij可以表示为每个矢量在参考坐标单位方向上投影的分量，因此旋转矩阵也可表示为如下形式：

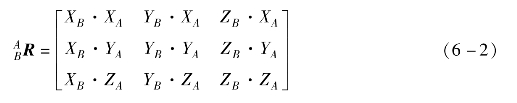
3.坐标系间的变换

（1）平移变换

在图6.4中，用矢量BP表示点P在坐标系｛B｝中的位置。坐标系｛B｝与参考坐标系｛A｝具有相同姿态，但经过了平移变换。以APB表示｛B｝的原点相对于｛A｝的位置，则P点在坐标系｛A｝中可表示为：

（2）旋转变换

在图6.5中，坐标系｛B｝与参考坐标系｛A｝的姿态不同，原点重合。用矢量BP表示点P在坐标系｛B｝中的位置，通过引入旋转矩阵ABR，可以给出P点相对于坐标系｛A｝的表示：

(www.xing528.com)

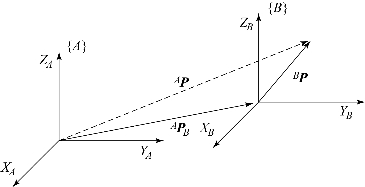
图6.4　平移变换

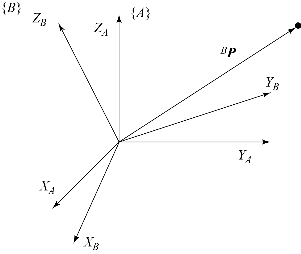
图6.5　旋转变换

下面考虑一般情况，如图6.6所示。坐标系｛B｝的原点与坐标系｛A｝的原点不重合，有一个矢量偏移APB，同时使用描述　｛B｝　相对于　｛A｝　的旋转。已知BP，求AP。

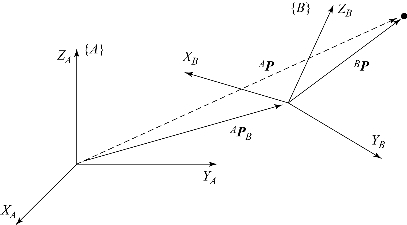
图6.6　一般情况下的矢量变换

首先将BP变换到中间坐标系，该坐标系与｛A｝的姿态相同，原点与｛B｝的原点重合。然后用中间坐标系通过平移变换到参考坐标系。根据上节旋转变换和平移变换可得：

将式（6-5）改写成矩阵形式：

其中的4×4矩阵被称为齐次变换矩阵。它以一种简单的矩阵形式表示了一般变换的平移和旋转。

（3）绝对变换和相对变换

在图6.7中，由坐标系｛3｝变换至坐标系｛1｝共有以下两种方式：

坐标系｛1｝～｛3｝初始位置相同，首先坐标系｛3｝相对于坐标系｛2｝和｛1｝旋转和平移，变换矩阵为。然后，坐标系｛3｝和｛2｝相对于坐标系｛1｝旋转和平移，变换矩阵为。两个齐次变换矩阵顺序左乘，得到坐标系｛3｝相对于坐标系｛1｝的齐次变换矩阵为。

坐标系｛1｝～｛3｝初始位置相同，首先坐标系｛2｝和｛3｝一起相对于坐标系｛1｝旋转和平移，此时变换矩阵为。然后，坐标系｛3｝相对于坐标系｛2｝旋转和平移，变换矩阵为。两个齐次变换矩阵顺序右乘，得到坐标系｛3｝相对于坐标系｛1｝的齐次变换矩阵为。

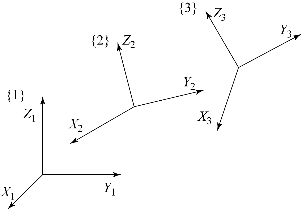
图6.7　一般坐标系间的变换

由此可以发现，坐标系在固定坐标系中发生连续齐次变换时，若变换是相对于固定坐标系的，则齐次变换矩阵为左乘，称为绝对变换；若变换是相对于自身坐标系当前位姿的，则齐次变换矩阵为右乘，称为相对变换。