由于求解常微分方程的解析解难度较大，甚至有时无法求解，所以在工程上往往求助于数值解。求解数值解是在特定点求解近似解的过程。常用的数值解法主要有欧拉（Euler）法和龙格-库塔（Runge-Kutta）法等。
1.欧拉（Euler）法
欧拉法是最简单的数值解法，在节点处用差商近似代替导数：
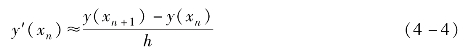
如此，推导出计算公式：
由于MATLAB中没有使用欧拉法求解的函数，但存在内部函数文件euler.m用于返回欧拉数和欧拉多项式，因此，在编写欧拉法的M文件时，需注意命名格式。
【例4.20】 在MATLAB中编写函数文件，实现欧拉法的功能。
在程序编辑窗口中编写以下语句，并以euler1.m为名存入相应的子目录。
【例4.21】 利用欧拉法求解初值问题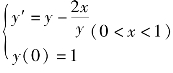
。
在命令行窗口中输入以下命令，并得出结果。
为了验证该方法的精度，求出该方程的解析解为y＝1+2x。
通过图像来直观地展示欧拉法精度：
欧拉法结果如图4.8所示。
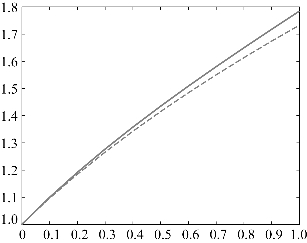
图4.8 欧拉法精度
2.龙格-库塔法
龙格-库塔法是求解常微分方程的经典方法，在MATLAB中提供了多个采用了该方法的函数命令，见表4.7。
表4.7 积分器
以上各种函数命令的主要调用方式如下。(www.xing528.com)
［T，Y］＝solver（odefun，tspan，y0）
［T，Y］＝solver（odefun，tspan，y0，options）
［T，Y，TE，YE，IE］＝solver（odefun，tspan，y0，options）
sol＝solver（odefun，［t0，tf］，y0…）
其中，solver，可以是上述积分器中的任一命令；odefun，定义了微分方程的形式；tspan，是一个区间，tspan＝［t0，tfinal］，定义微分方程的积分区间；y0，初始条件；options，参数的设置要使用odest函数命令，其调用格式如下。
options＝odeset（'name1＾'，value1，'name2＾'，value2，…）：创建一个参数结构，对指定的参数名进行设置，未设置的参数将使用默认值。
options＝odeset（oldopts，'name1＾'，value1，…）：对已有的参数结构oldopts进行修改。
options＝odeset（oldopts，newpots）：将已有参数结构oldpots完整转换为newopts。
odeset：显示所有参数的可能值与默认值。
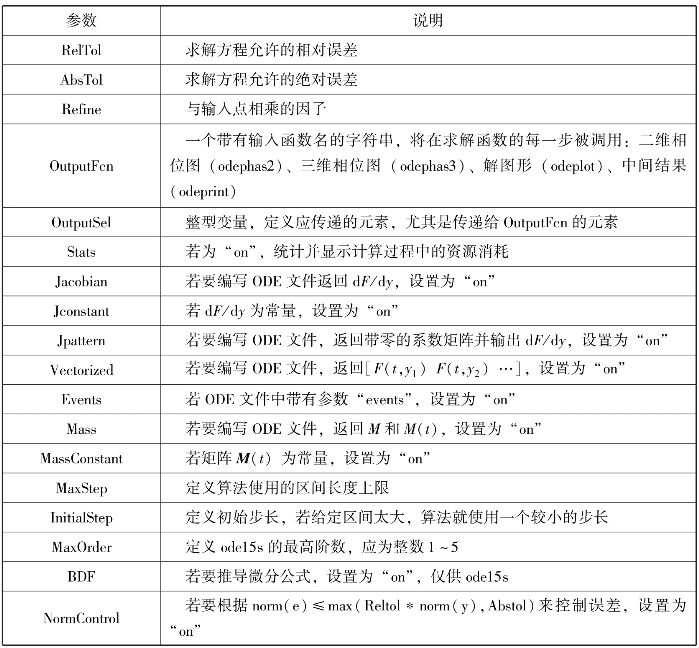
options具体的设置参数见表4.8。
表4.8 设置参数
【例4.22】 利用龙格-库塔法求解初值问题
。
在程序编辑窗口中编写以下语句，并以g.m为名存入相应的子目录。
在命令行窗口中输入以下命令，并得出结果。
为了验证该方法的精度，求出该方程的解析解为y＝1+2x。
通过图像来直观地展示龙格-库塔法精度：
龙格-库塔法结果如图4.9所示。
图4.9 龙格-库塔法精度
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
