如何在MATLAB中求函数零点及其他数值？

对于函数f（x）而言，求零点即求方程f（x）＝0的解；而对于多项式，则可以用roots函数来求解。单变量函数的零点可以用fzero函数进行求解，其调用格式如下：

x＝fzero（'fun＾'，x0），x＝fzero（fun，［x1，x2］）：寻找x0附近或区间　［x1，x2］内函数fun的零点，返回该点的x坐标。

x＝fzero（'fun＾'，x0，tol，trace），x＝fzero（fun，［x1，x2］，tol，trace）：tol代表精度，可以缺省，缺省时，tol＝0.001。trace＝1，迭代信息在运算中显示；trace＝0，不显示迭代信息，默认值为0。

［x，fval］＝fzero（…）：返回零点的x坐标的同时返回该点的函数值。

［x，fval，exitflag］＝fzero（…）：返回零点的x坐标、该点的函数值及程序退出的标志。

［x，fval，exitflag，output］＝fzero（…）：返回零点的x坐标、该点的函数值、程序退出的标志及选定的输出结果。

【注】fzero命令不仅可以求零点，而且可以求函数等于任何常数数值的点。

【例4.14】　求x2-4＝0的零点。

在MATLAB的命令行窗口中输入以下命令：

MATLAB会出现相应的结果：

此处，f（x）＝x2-4是一个多项式，所以可以使用roots函数求出相同的零点，在MATLAB的命令行窗口中输入以下命令：

(www.xing528.com)

MATLAB会出现相应的结果：

【例4.15】　求的零点。

在MATLAB中输入以下命令，建立函数M文件f.m，存入相应的子目录。

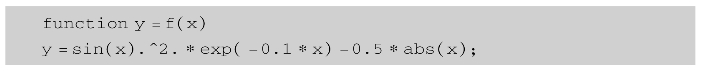
在程序编辑窗口中编写以下语句，并命名为fzero_example.m。

在MATLAB的命令行窗口中输入以下命令：

MATLAB会出现相应的结果：

零点分布图如图4.7所示。

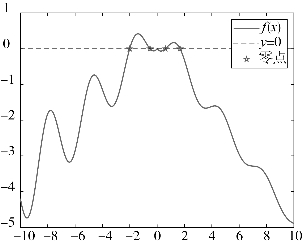
图4.7　零点分布图