MATLAB实现拉格朗日插值法的数据推断

数据插值可用来根据已知数据推断未知数据。插值运算是根据数据的分布规律，寻找一个可以连接已知各点的函数表达式，并利用该函数表达式预测两点之间任意位置上的函数值。

定义：设函数y＝f（x）在区间［a，b］上有意义，且已知y在n+1个节点a≤x0＜x1＜…＜xn≤b上的值为y0，y1，…，yn。若存在简单函数P（x），使P（xi）＝yi（i＝0，1，…，n）成立，就称P（x）为f（x）关于节点x0，x1，…，xn的插值函数，点x0，x1，…，xn称为插值节点，包含插值节点的区间［a，b］称为插值区间，而f（x）称为被插值函数，求插值函数P（x）的方法称为插值法。

数值插值有拉格朗日（Lagrange）插 值、埃 尔米特（Hermite）插值、牛顿（Newton）插值、分段线性插值和三次样条插值等，下面对其中部分插值方法进行介绍。

1.拉格朗日（Lagrange）插值

对给定的n个插值点x1，x2，…，xn及对应的函数值y1，y2，…，yn，利用构造的n-1次拉格朗日插值多项式，则对插值区间内任意x的函数值y，可通过式（4-1）求得：

由于MATLAB中没有现成的拉格朗日插值命令，下面来编写M文件实现该功能。

【例4.1】　在MATLAB中编写函数文件，实现拉格朗日插值法的功能。

在程序编辑窗口中编写以下语句，并以lagrange.m为名存入相应的子目录。

【例4.2】　给出f（x）＝ln（x）的数值表（表4.1），用拉格朗日插值法在［0.1，0.8］区间以0.01为步长进行插值。

表4.1　f（x）＝ln（x）的数值表

利用拉格朗日函数，可以直接在MATLAB命令行窗口中输入下面的命令，并得出结果。

所得插值结果如图4.1所示。

从图4.1可以看出，拉格朗日插值法的一个特点就是：拟合出的多项式图形通过每一个测量数据点。

2.埃尔米特（Hermite）插值

埃尔米特插值法既保证了拟合多项式在节点上的函数值相等，又保证了节点对应的导数值甚至高阶导数值也相等。

对给定的n个插值节点x1，x2，…，xn和对应的函数值y1，y2，…，yn，以及一阶导数值y1′，y2′，…，yn′，在插值区域内任意x的函数值y见式（4-2）。

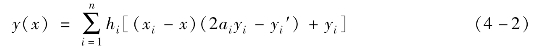
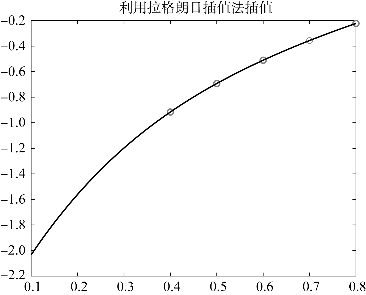
图4.1　拉格朗日插值法

其中，　

由于MATLAB中没有现成的埃尔米特插值命令，下面来编写M文件实现该功能。

【例4.3】　在MATLAB中编写函数文件，实现埃尔米特插值法的功能。

在程序编辑窗口中编写以下语句，并以hermite.m为名存入相应的子目录。

【例4.4】　已知某次实验中测得的某质点的速度和加速度变化见表4.2，求质点在时刻t＝1.2处的速度。

表4.2　某次实验中测得的某质点的速度和加速度变化

(www.xing528.com)

利用埃尔米特函数，可以直接在MATLAB命令行窗口中输入下面的命令，并得出结果。

插值结果如图4.2所示。

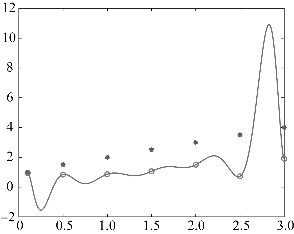
图4.2　埃尔米特插值法结果

3.分段线性插值

通常情况下，函数插值的次数越高，精度越高。实际情况下，当次数增大时，有时会在两端产生激烈的震荡，出现函数不收敛的现象，这种高次插值的病态现象被称为Runge现象。

【例4.5】　在区间［-5，5］上的各阶导数存在，但在此区间上的拉格朗日插值多项式在全区间上并非都收敛。取n＝10，用拉格朗日插值法进行插值计算。

在MATLAB的命令行窗口中输入以下命令并得出结果

输出图形结果如图4.3所示。

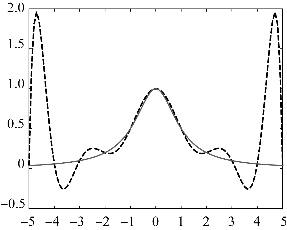
图4.3　Runge现象

针对Runge现象，人们通过插值点用折线或低次曲线连接起来逼近原曲线，这就是分段线性插值。插值多项式的次数叫作插值的阶。如果插值点位于插值区间内，这种插值过程叫作内插，否则叫作外推。

MATLAB为用户提供了interp1函数来实现分段线性插值，其具体调用格式如下：

i＝interp1（x，Y，xi）：对一组节点（x，Y）进行插值，计算插值点xi的函数值。x为节点向量值，Y为对应节点函数值；如果Y为矩阵，则插值对Y的每一列进行；如果Y的维数超过x或xi的维数，返回NaN。

yi＝interp1（Y，xi）：对一组节点（x，Y）进行插值，计算插值点xi的函数值。x为节点向量值，Y为对应节点函数值；如果Y为矩阵，则插值对Y的每一列进行；如果Y的维数超过x或xi的维数，返回NaN。

yi＝interp1（x，Y，xi，method）：method是插值使用的算法，默认为线性算法，其值可以是以下几种：‘nearest’，线性最近项插值；‘linear’，线性插值；‘spline’，三次样条插值；‘pchip’，分段三次埃尔米特插值；　‘cubic’，与‘pchip’相同。其中，对于‘nearest’和‘linear’两种方法，如果xi超出x的范围，返回NaN；而对于其他几种方法，系统将对超出范围的值进行外推计算，见表4.3。

表4.3　外推计算

【例4.6】　在区间［0，10］内对cos（x）进行分段线性插值。

在MATLAB的命令行窗口中输入以下命令，并得出结果。

余弦分段插值结果如图4.4所示。

【例4.7】　利用分段插值解决例4.5的Runge现象。

在MATLAB的命令行窗口中输入以下命令，并得出结果。

分段线性插值结果如图4.5所示。

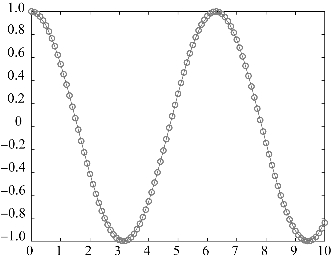
图4.4　余弦分段插值

图4.5　分段线性插值