符号微积分介绍与应用

1.符号极限

在MATLAB中求函数极限的函数是limit，可用来求函数在指定点的极限值和左右极限值。对于极限值为“没有定义”的极限，MATLAB给出的结果为NaN；极限值为无穷大时，MATLAB给出的结果为inf。limit函数的调用格式如下：

limit（f）：计算，其中，f是符号函数；

limit（f，x，a）：计算l，其中，f是符号函数；

limit（f，x，inf）：计算，其中，f是符号函数；

limit（f，x，a，'right'）：计算，其中，‘right’表示变量从右边趋近于a，f是符号函数；

limit（f，x，a，'left'）：计算，其中，‘left’表示变量从左边趋近于a，f是符号函数。

【例2.42】　求下列极限。

（1）　（2）

（3）　（4）

极限（1）的求解：

极限（2）的求解：

极限（3）的求解：

极限（4）的求解：

2.符号导数

（1）函数的导数和高阶导数

diff函数用于对符号表达式求导，一般调用格式如下：

y＝diff（f）：默认以x为自变量求f的一阶导数，其中，f为符号函数；

y＝diff（f，'z'）：以z为自变量求导数，默认为1阶，其中，f为符号函数；

y＝diff（f，x，n）：默认x为自变量求n阶导数，其中，f为符号函数。

【例2.43】　求函数的一阶导数和函数y＝cosx2的三阶导数。求f′（x）：

求y‴：(www.xing528.com)

（2）多元函数的偏导

已知二元函数f（x，y），求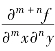，调用格式：

f＝diff（diff（f，x，m），y，n）

f＝diff（diff（f，y，n），x，m）

【例2.44】　求的偏导数。

z对x的偏导：

z对y的偏导：

3.符号积分

高等数学中求符号积分是较费时间的事情，MATLAB提供了快速求出符号积分的函数供用户使用，符号积分由函数int来实现，一般调用格式为：

int（f）：求函数f对默认变量的不定积分，用于函数只有一个变量；

int（f，v）：以v为自变量，求函数f的不定积分；

int（f，v，a，b）：求函数f在（a，b）上的定积分，其中a，b分别表示定积分的下限和上限。

【例2.45】　分别求下列积分。

（1）求∫f（x）dx。

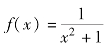（2），求。

（3）F（x，y，z）＝+4x4sin（x2y）y2+4cos（x2y）x4y2-sin（x2y）］，求∭F（x，y，z）dx2dydz。

积分（1）的求解：

积分（2）的求解：

积分（3）的求解，积分顺序为z→y→x→x：

积分（3）的求解，积分顺序改为z→x→x→y：

显然，f1和f2的最简形式相同，MATLAB中积分顺序不同不影响最终的最简积分结果。