符号对象的运算方式

1.符号矩阵

（1）创建符号矩阵

【例2.36】　分别使用函数sym和syms创建符号矩阵。

sym函数创建符号矩阵：

方法1：

方法2：

syms函数创建符号矩阵：

（2）符号矩阵运算

【例2.37】　符号矩阵运算。

求符号矩阵的转置：

求符号矩阵的逆：

求符号矩阵的行列式：

符号矩阵的运算不限于线性代数中的求逆、求行列式等，还涉及特征向量、奇异值、Jordan标准型等的运算。实现方式如下。

符号矩阵的特征值、特征向量运算：可以通过函数eig，eigensys来实现；

符号矩阵的奇异值运算：可以通过函数svd，singavals来实现；

符号矩阵的Jordan标准型运算：可以通过函数jordan来实现。

2.符号多项式

（1）符号多项式与多项式系数向量之间的转换(www.xing528.com)

【例2.38】　符号多项式与多项式系数向量之间的转换。

sym2poly函数的使用：

poly2sym函数的使用：

（2）符号多项式运算

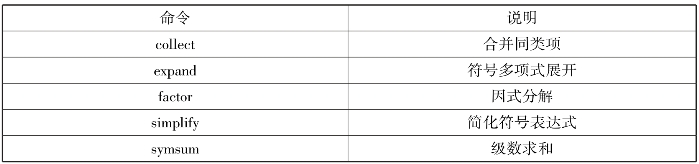
常用的5种运算命令见表2.11。

表2.11　符号表达式的简化

【例2.39】　符号多项式运算。

因式分解（factor函数）：

多项式展开（expand函数）：

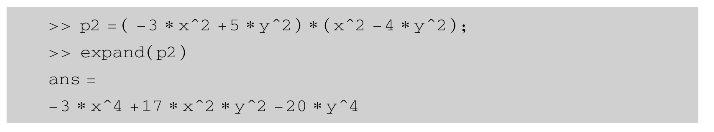
简化多项式（simplify函数）：

3.符号方程求解

MATLAB用solve函数求解符号方程。如果表达式不是一个方程（无等号），则在求解之前自动将表达式的值设置为0。solve函数可求解f（x）＝0或y（x）＝f（x）两种形式的代数方程。

【例2.40】　求解方程f（x）＝0。

用solve函数求解：

【例2.41】　求解方程y（x）＝f（x）。