多项式运算技巧总结

多项式运算是线性代数和线性系统分析中的重要内容。MATLAB提供了多条命令，可以进行多项式运算。MATLAB语言把多项式表达成一个行向量，该向量中的元素是按多项式降幂排列的，多项式的阶次是依照系数向量p的长度减1而得的。表2.9是MATLAB中常用的多项式函数。

表2.5　三角函数

表2.6　指数运算函数

表2.7　复数运算函数

表2.8　圆整和求余函数

表2.9　多项式函数

【例2.22】　建立并显示多项式p（x）＝x4+3x3-2x2+5。

在MATLAB命令行窗口中输入：

结果显示如下：

再利用polysym函数将多项式显示：

1.多项式的四则运算

（1）多项式的加减法

两个多项式的加法、减法为多项式元素的加、减运算。两个多项式的阶数可以不同，但在定义多项式时，应当补充0元素使其行向量元素数目相等，否则不能相加、减。

【例2.23】　多项式加减法运算。

输入p1，p2：

进行加减运算的结果如下：

（2）conv多项式乘运算

【例2.24】　a（x）＝x2+2x+3，b（x）＝4x2+5x+6，求c＝（x2+2x+3）（4x2+5x+6）。

输入a，b：

计算conv（a，b）：

（3）deconv多项式除运算

【例2.25】　多项式除运算示例。

输出余数显示：

2.多项式微分与积分

（1）多项式微分

MATLAB提供了polyder函数用于计算微分，调用格式如下：

k＝polyder（p）：求多项式p的微分；

k＝polyder（a，b）：求多项式a，b乘积的微分；

［q，d］＝polyder（a，b）：求多项式a，b商的导数，导数的分子存入q，分母存入d。(www.xing528.com)

上述函数中，参数p，a，b均为多项式的系数向量，结果k，q，d也是多项式的系数向量。

【例2.26】　求f（x）＝x4+2x3+3x2+4x+5的导数。

将结果b显示为符号多项式：

即得f′（x）＝4x3+6x2+6x+4。

【例2.27】　求有理分式的导数。

即得。

（2）多项式积分

MATLAB提供了polyint函数计算积分，其调用格式如下：

q＝polyint（p，k）：返回多项式p的积分，设积分的常数项为k；

q＝polyint（p）：返回多项式p的积分，设积分的常数项为0。

【例2.28】　已知f（x）＝x3+2x2+5x+7，求其积分表达式，考虑积分常数为0。

即得。

3.多项式的值

MATLAB提供了两种求多项式值的函数：polyval与polyvalm，它们的输入参数均为多项式的系数向量p和自变量x。两者的区别在于前者是代数多项式求值，而后者是矩阵多项式求值。

（1）代数多项式求值

polyval函数用来求代数多项式的值，其调用格式为：

若x为一数值，则求多项式在该点的值；若x为向量或矩阵，则对向量或矩阵中的每个元素求其多项式的值。

【例2.29】　已知多项式3x4-7x3+2x2+x，分别计算x＝2.5及x取1～6时多项式的值。

（2）矩阵多项式求值

polyvalm函数用来求矩阵多项式的值，其调用格式与polyval的相同，但含义不同。polyvalm函数要求X为方阵，它以方阵为自变量求多项式的值。设X为方阵，p代表多项式2x2+x+1，那么polyvalm（p，X）的含义为：

而polyval（p，X）的含义为求X中每个元素多项式p的值。

【例2.30】　已知多项式x3+2x-1，以矩阵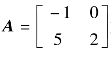为自变量，分别用函数polyval和polyvalm求多项式的值。

4.多项式的根

n次多项式具有n个根，这些根可能是实根，也可能含有若干对共轭复根。MATLAB提供的roots函数用于求多项式的全部根，其调用格式为：

其中，p为多项式的系数向量，求得的根赋给向量r，即r（1），r（2），…，r（n）分别代表多项式的n个根。

若已知多项式的全部根，则可以用poly函数建立起该多项式，其调用格式为：

其中，r为具有n个元素的向量。poly（r）建立以x为其根的多项式，且将该多项式的系数赋给向量p。

【例2.31】　已知f（x）＝2x4-4x3+3x-1，

（1）计算f（x）＝0的全部根。

（2）由方程f（x）＝0的根构造一个多项式g（x）。

即g（x）＝x4-2x3+1.5x-0.5，显然g（x）和f（x）成倍数关系。