矩阵的生成和访问方法

1.矩阵生成

（1）直接输入简单矩阵

对于简单矩阵来说，直接输入法创建矩阵是一种最直接、简单、有效的方法。直接创建矩阵时，必须满足以下4个条件：

矩阵元素必须用［］括住；

矩阵元素必须用逗号或空格分隔；

在［］内，矩阵的行与行之间必须用分号分隔；

矩阵元素可以为表达式，也可以为复数。

【例2.1】　直接创建矩阵。

使用空格（或逗号）创建矩阵：

使用冒号快捷创建矩阵：

【注】冒号是一个重要的运算符，利用它可以创建行向量。冒号表达式的一般格式为a：b：c，其中，a为初值，b为步长，c为终值（c＞a）。另外，表达式中省略b时，默认步长为1。

快捷创建一维数组：

创建复数矩阵：

（2）矩阵生成命令

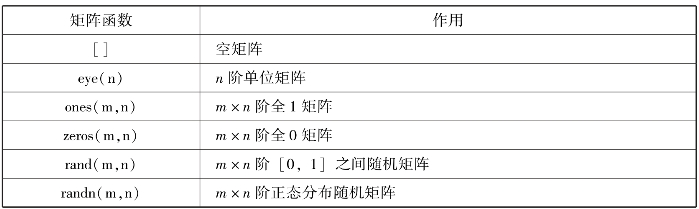
MATLAB内部提供了一些特殊矩阵的生成命令可供用户快捷使用，可以用于快速创建一些特殊矩阵，如单位矩阵和零矩阵等，见表2.1。

表2.1　常用矩阵生成命令

【例2.2】　建立一个3×3零矩阵zeros（3）。

【例2.3】　建立一个3×2零矩阵zeros（3，2）。

【例2.4】　设A为2×3矩阵，则可以用zeros（size（A））建立一个与矩阵A同样大小的零矩阵。

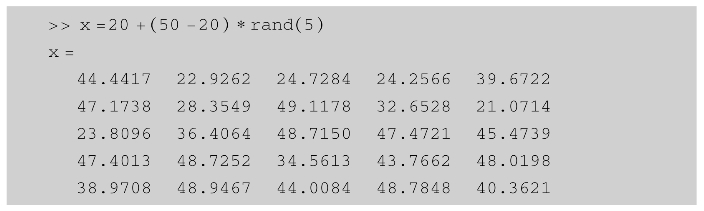
【例2.5】　建立在区间［20，50］内均匀分布的5阶随机矩阵。

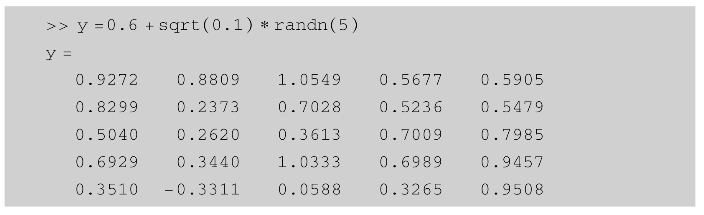
【例2.6】　建立均值为0.6、方差为0.1的5阶正态分布随机矩阵。

此外，常用的函数还有reshape（A，m，n），它在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵。

（3）从外部数据文件读取

【例2.7】　外部载入dat文件创建矩阵。(www.xing528.com)

【注】dat文件并不是一种标准文件，但按照扩展名.data来看即为数据文件，用于存储大批量数据，此处load指令的作用是将dat文件中的变量加载到工作区。

（4）用户编写M文件产生矩阵

【例2.8】　对于比较大、比较复杂的矩阵，可以为其专门建立一个M文件。

新建M文件（详见第3章），输入：

命令行窗口中运行：

【注】M文件是一种扩展名为“.m”的MATLAB程序，可根据调用方式不同分为两类：脚本文件和函数文件，该例题中创建的M文件为脚本文件。

（5）魔方矩阵

魔方矩阵有一个有趣的性质，其每行、每列及两条对角线上的元素和都相等。对于n阶魔方矩阵，其元素由1，2，3，…，n2共n2个整数组成。MATLAB提供了建立魔方矩阵的函数magic（n），其功能是生成一个n（≥3）阶魔方矩阵。

【例2.9】　创建5×5魔方矩阵。

2.矩阵元素访问

使用矩阵元素的行列全下标形式A（∗，∗）。使用全下标形式访问矩阵元素的方法简单、直接，同线性代数的矩阵元素的概念一一对应。

使用矩阵元素的单下标形式A（∗）。矩阵元素的单下标是矩阵元素在内存中存储的序列号，一般情况下，同一个矩阵的元素存储在连续的内存单元中（元素的排列以列元素优先）。

【例2.10】　矩阵与元素访问示例。

矩阵单个元素访问：

矩阵块访问：

矩阵元素访问“：”的使用：

主要矩阵访问方式见表2.2，其中矩阵元素单下标和全下标可运用MATLAB的两个函数sub2ind和ind2sub进行计算。

表2.2　矩阵元素访问常用指令

【例2.11】　矩阵的单下标与全下标。

sub2ind函数的使用：

ind2sub函数的使用：