旋转相量法的应用

相量是复平面上以角速度ω逆时针绕原点旋转的有向线段。它可以表示任意时刻正弦量的三要素，旋转相量法必须做如下规定：正弦量的最大值即为旋转相量的长度；正弦量的初相位即为旋转相量与横轴正向的夹角；正弦量的角频率即为旋转相量随时间t逆时针旋转的角速度。则在任一瞬间，旋转相量在纵轴上的投影就等于该正弦量的瞬时值，如图2.5所示。

图2.5　正弦波与旋转相量的关系

相量逆时针旋转的角速度，正好是正弦量的角频率ω；相量的模正好对应正弦量的幅值；相量任意时刻在虚轴上的投影正好是正弦量的瞬时值；相量的辐角正好是正弦量的初相角。所以任意一个正弦量总可以用一个相量与其对应，相量的模对应正弦量的幅值（或有效值）相量的辐角对应正弦量的初相角。在相量图中一般只画它的起始位置，但应理解它是以角频率ω逆时针连续旋转的，它的位置与时间有关，在经过时间t，才转到虚线位置，所以，说它是时间相量。在同一电路中，各个正弦量都是同频率旋转，它们之间的相对位置（即相位差）保持不变。因此，只要用旋转相量的初始位置来表示正弦量就可以了，我们把这种表示正弦量的方法称相量法。正弦量用相量表示所作的图称相量图。如果相量线段的长度等于正弦量的有效值，就称为正弦量的有效值相量，但该相量在纵轴上的投影就不是瞬时值。

相量可以用大写字母上加一点表示，例如就表示电压有效值相量和电流有效值相量。表示电压幅值相量和电流幅值相量。相量可以用复数式、三角式、指数式和极坐标式四种形式来表示。

1.复数的表示方法

一个复数可以用以下几种形式来表示：

（1）直角坐标形式。

a为复数的实部，b为复数的虚部，j为虚单位，j2=-1。如图2.6所示。

复数在复平面上还可以用向量表示，如图2.7所示。向量的长度r称为复数A的模，用｜A｜表示。向量与实轴的夹角，称为复数的辐角，用φ表示。

图2.6　复平面上的点

图2.7　复平面上的向量

（2）三角形式。

其中，。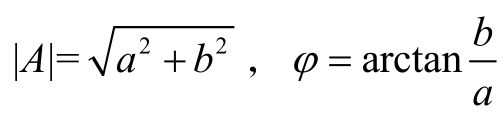

（3）指数形式。

在电工技术中还常把复数写成如下的极坐标形式

2.复数的运算

在一般情况下，相量的乘除运算用指数式或极坐标式进行。

设有相量

则

相量相乘除的几何意义如图2.8所示。(www.xing528.com)

把模等于1的相量如等称为旋转因子，例如把任意相量乘以就等于把相量在复平面上逆时针旋转（见图2.9），表示为，故把j称为旋转90°的旋转因子。

图2.8　相量的乘除运算

图2.9　旋转因子

例2.1　设已知两个正弦电流分别为i1=70.7sin（314 t-30°）　A；i2=60sin（314 t+60°）　A，求i=i1+i2。

解：同频率正弦量的相加（或相减）所得的和（或差）仍是一个频率相同的正弦量。

i=i1+i2

设

i=Imsin(314 t+θ)　A

有

Imsin(314 t+θ)=70.7sin(314 t-30°)+60sin(314 t +60°)

用相量来表示i、i1、i2

把正弦量的运算转换成对应的相量代数运算，有式

也可表示为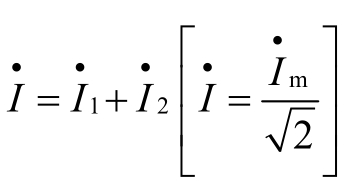

通过写出对应的正弦量

通过上面的例子，可知：

① 只有对同频率的正弦量，才能应用对应的相量来进行代数运算。

② 在应用相量分析法时，先将正弦量变换为对应的相量，通过相量的代数运算求得所求正弦量对应的相量，再由该相量写出对应的正弦量的瞬时表达式。

③ 同样可推广到多个同频率的正弦量运算，转换成对应相量的代数运算，如基尔霍夫定律的相量表达形式：