摩擦圆盘角分度装置精度分析

摩擦圆盘角分度装置的一个优点是具有将圆光栅误差按传动比线性缩小的功能，并可通过调整速比将测角误差控制在所需的范围之内。其已在国内外精密机械或测量机构中广泛采用。

由于精密测角是在传动状态下进行的，因此，影响摩擦圆盘角分度装置测角精度的主要因素有两个：一是两个对滚摩擦圆盘各自的形状误差及相对于各自回转轴线的偏心；二是两摩擦圆盘之间打滑的影响。

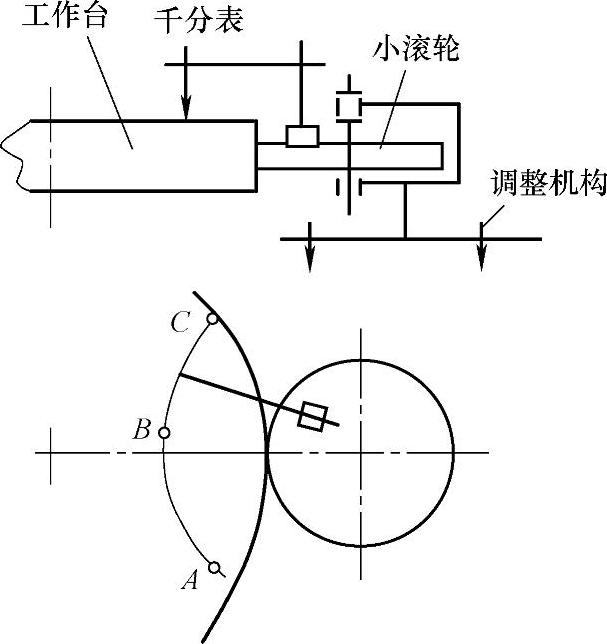
图5-10 测角装置对正调整

1.工作台外侧基准圆柱面形状误差的影响

设R为工作台公称半径，r为精密摩擦圆盘的公称半径，q为传动比，在理想无误差情况下：

Rφ=rθ （5-12）

式中，φ为工作台转角；θ为摩擦圆盘转角。

则有

当两滚圆盘有几何形状误差时，q已不是常数。因两滚圆盘接触是一条窄带，可认定其几何形状误差为各自的圆度误差，其半径的变化量影响传动比q的变化。考虑到摩擦圆盘的制造精度很高，误差可忽略不计。而与其对滚的机床工作台外侧基准圆柱面的圆度误差成为影响测量精度的主要因素。按照圆度误差具有径向性和周期性的几何特征，工作台外侧基准圆柱面的半径是转角φ的函数，可在极坐标系中用富氏级数展开表达为

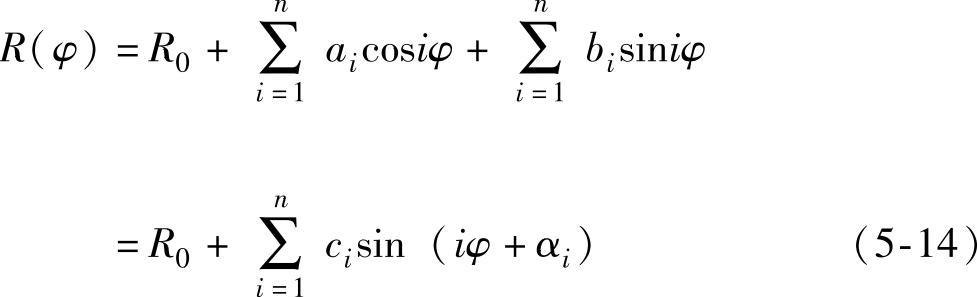
式中，R（φ）为任一φ角时的向量半径；R₀为富氏级数的常量，表示圆的平均半径；a_i、b_i为富氏系数；α_i为初始相位。且有

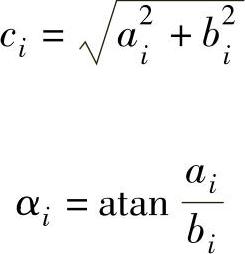
式（5-14）的实际意义可看成是由一个平均半径为R₀的圆周和若干个按不同周期变化的形状误差波形叠加而成的。

当i=1时，级数展开式中的a₁cosφ+b₁sinφ项表明由R₀决定的平均半径圆的圆心相对于工作台回转中心偏心，即工作台外侧基准圆柱面的中心位置偏离，其偏心量为

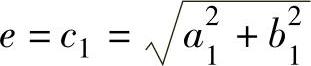
初始相位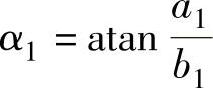

当i=2时，级数展开式中的a₂cos2φ+b₂sin2φ项表明工作台外侧基准圆柱面呈椭圆形状；i=3，则表明呈三棱圆形状；依此类推，n次谐波，则表明在极坐标系中是一个n棱圆。

根据圆度误差的国标定义，偏心、表面粗糙度（高次谐波分量）和表面波度的影响均应从R（φ）中剔除，所以，工作台外侧基准圆柱面的圆度误差函数可表示为

忽略测角装置摩擦圆盘形状误差的影响，并认为两滚圆盘做无滑动的纯滚动，由式（5-12）可以有

R（φ）dφ=rdθ （5-16）

积分得

∫R（φ）dφ=∫rdθ+C₀ （5-17）

即

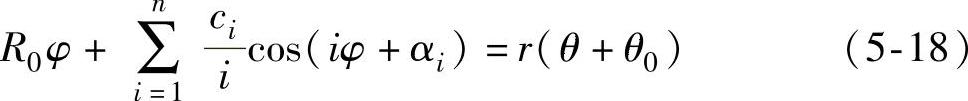
这里的C₀或θ₀对研究无影响，故将其忽略。同时，若不考虑工作台外侧基准圆柱面的中心相对于工作台回转中心的偏心，即R=R₀，于是φ与θ的关系为

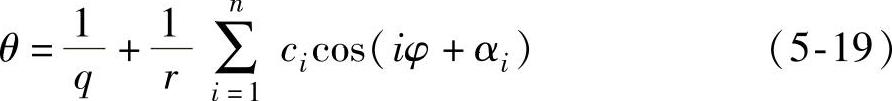
式（5-19）实际上给出了两轮在纯滚动条件下的圆光栅转角与工作台转角的关系。其中等号右端第一项为理想的φ与θ的线性转角关系；第二项为误差对转角关系的影响，表现上述工作台外侧基准圆柱面的圆度误差（径向周期误差）的影响。

在测量中，θ由圆光栅读出（示值），此示值乘以q所得到的即为工作台的实际转角示值φ′，利用式（5-12）、式（5-13）、式（5-19）有(www.xing528.com)

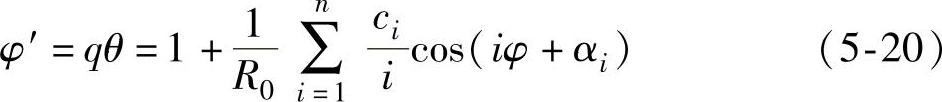
进一步地

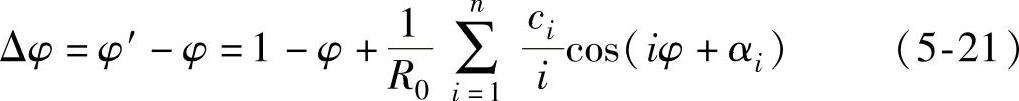
式（5-21）即为在工作台外侧基准圆柱面圆度误差影响下的角度折算误差。分析可见，由于工作台的半径很大（实际利用的工作台直径为3600mm），因此，分母上的R₀对抑制误差Δφ是有利的。此外，以c_i为幅值的周期误差，随频率i的增加而递减。可以看出，其对测角精度的影响主要表现在低次谐波，即i=1、i=2、i=3、i=4时。由前述可知，当i=1时，工作台外侧基准圆柱面中心对工作台回转中心的偏心量为

式中，Δ为工作台外侧基准圆柱面对工作台回转中心的径向跳动量。

依据实测，机床工作台的径向跳动量为0.015mm，则e=0.075mm。此时，其在一周内对测角精度的影响为e/R=8.3×10^-6（弧度）=1.72″。由此可见，工作台外侧基准圆柱面对工作台回转中心偏心误差的影响相对很小。而对齿廓偏差和螺旋线偏差的测量，由于工作台转角并不很大（如对于模数为20mm，齿数为200的齿轮的单个轮齿廓面展开角度约为4°，e带来的齿廓偏差测量误差为0.172μm），完全可以忽略。因此，工作台外侧基准圆柱面形状误差对测量精度的影响是很小的。

由工作台外侧基准圆柱面形状误差的影响而产生的测角误差Δφ对齿廓偏差测量精度的影响为

Δφ=ΔφR_b （5-23）

式中，R_b为齿轮基圆半径。

2.“弹性蠕滑”对测角精度的影响

参见图5-9，测角装置的摩擦圆盘是在弹簧压力作用下与工作台外侧基准圆柱面产生弹性接触，依靠它们之间的摩擦力被驱动的。当此驱动力小于小摩擦圆盘机构的阻力矩时，将产生打滑现象，一般称为宏观打滑。这一点因为小摩擦圆盘机构轴系的阻力矩很小，在测量过程中一般不会出现。值得重视的应是微观打滑问题，即“弹性蠕滑”。所谓“弹性蠕滑”，是指在不产生宏观的打滑的情况下，对滚的两轮接触区内产生的弹性变形引起的微滑。这一点其他文献已做了深入的研究，并且给出了关于弹性蠕滑率的公式：

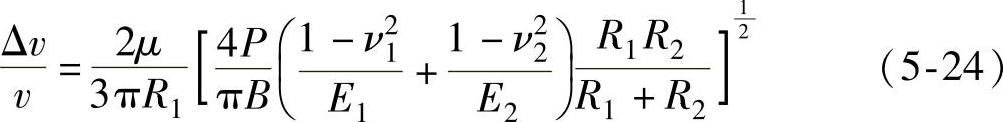
式中，P为两个圆盘之间的法向压紧力（N）；B为两个圆盘的接触宽度（m）；R₁为主动圆盘半径（m）；R₂为从动圆盘半径（m）；E₁为主动圆盘材料的弹性模量（N/m²）；E₂为从动圆盘材料的弹性模量（N/m²）；

ν₁为主动圆盘材料的泊松比；ν₂为从动圆盘材料的泊松比；μ为两轮间的滑动摩擦因数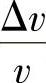；为弹性蠕滑率。

实际在机测量中，机床工作台外侧基准圆柱面（主动圆盘）的宽度为50mm；半径R₁=1800mm；材料的弹性模量E₁=160×10⁹N/m²；材料的泊松比ν₁=0.25。

所设计制造的测角装置摩擦圆盘宽度（即实际接触宽度B）为40mm；半径R₂=180mm；材料的弹性模量E₂=205×10⁹N/m²；材料的泊松比ν₂=0.26。

两个圆盘之间的滑动摩擦因数μ=0.3；两个圆盘之间的正压力P=25N。

若测量中两个圆盘滚过的弧长为S，在此之间产生的弹性蠕滑，即“打滑”的弧长为ΔS，则有：

依据式（5-24）、式（5-25）做“弹性蠕滑”验算如下：

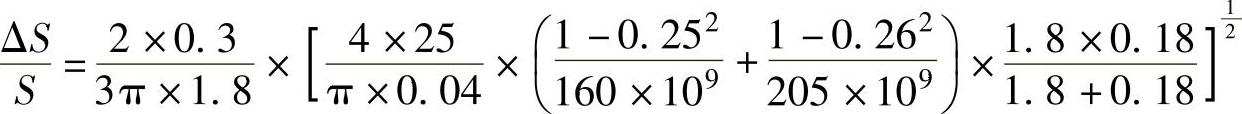
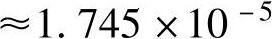
上式计算中，S=3600×πμm=1.131×10⁷μm，则工作台旋转一周产生的弹性蠕滑ΔS=197.4μm，此值实际表明了被测大齿轮转动一周时，“弹性蠕滑”产生的测角圆光栅示值累计误差。而测量时，被测齿轮转动角度很小（基本在4°左右），由“弹性蠕滑”产生的转角误差也很小（≈2.2μm），对测量结果影响很小，基本可以忽略。

由“弹性蠕滑”产生的转角误差在测量齿轮一个轮齿廓面对齿廓偏差时对测量精度的影响为

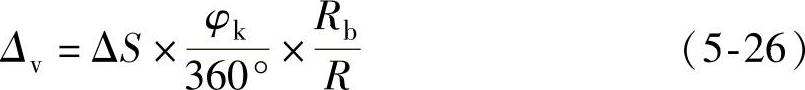
式中，φ_k为测量一个轮齿廓面的齿廓偏差时齿轮的转角；R_b为齿轮基圆半径；R为机床工作台外侧基准圆柱面的半径。

则由测角装置引起的测量误差为