误差模型及其应用于齿轮直母线偏差的求解

令Z=Z^∗，将它与φ₁或φ₂代入式（4-20），可求得Y，进而可求得沿渐开线法线方向的误差，即直母线偏差为

δF（λ，Z）=（Y^∗-Y）cos（α+φ₂） （4-21）

由此，可获得三维数组（λ，Z，δF），参数λ、Z分别为齿廓参数和直母线参数，δF为对应点误差。

下面分别讨论这两种测量方案。

（1）被测齿轮转动分度测量（方案一） 此时，φ₂=0°式（4-19）可化为

可以看出，上面的参数Y、Z为齿条的移动量，u为齿条测头上啮合点位置量。三者实质为参数φ₁、v的函数。

由式（4-22）中的第三式可得

将上式与λ的表达式一起代入式（4-22）中的第一式，可得

当φ₁确定时，Y为Z的函数，二者坐标的合成确定了一条理论直母线。

当φ₁改变时，Y与Z的合成确定了廓面上的不同的直母线，构成直母线族。

在实际测量时，当φ₁确定时，可测量实际直母线参数Y^∗和Z^∗。(www.xing528.com)

令Z^∗=Z，对应的δF即为直母线上某点处沿渐开线法线方向的误差。

（2）齿条测头转动分度测量（方案二） 此时，φ₁=0°式（4-19）可化为

可以看出，上面的参数Y、Z、u实质为参数φ₂、v的函数。

将v、λ的表达式一起代入式（4-24）中的第一式，可得

后面的计算过程同方案一。

下面进行齿廓偏差与螺旋线偏差分离。

1）齿廓偏差。令Z=Z₀，为常数，标志是某一截面的渐开线齿廓，对应的二维数组（λ，δF）即为齿廓偏差。

2）螺旋线偏差。令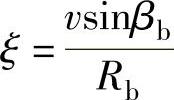，根据对式（2-32）的分析，当ζ=λ-ξ为常数时，描述曲面上半径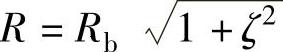的螺旋线，此时有

由式（4-26）可求得函数关系Z=Z（λ，R）。根据齿轮的参数，首先假设要求的螺旋线所在的圆柱直径R=R₀，进而通过函数关系Z=Z（λ，R₀）在三维误差数组中确定的二维数组[Z（λ，R₀），δF]即为螺旋线偏差。