理想条件下的啮合过程优化

为了研究方便，以下将建立适用于上述两种测量方案的啮合方程，并做规定：小写表示运动后的矢径与标架。假设刃边齿条沿齿轮的Y、Z两轴线平移，齿轮与齿条绕各自的Z轴做分度运动，于是有：

（1）齿轮

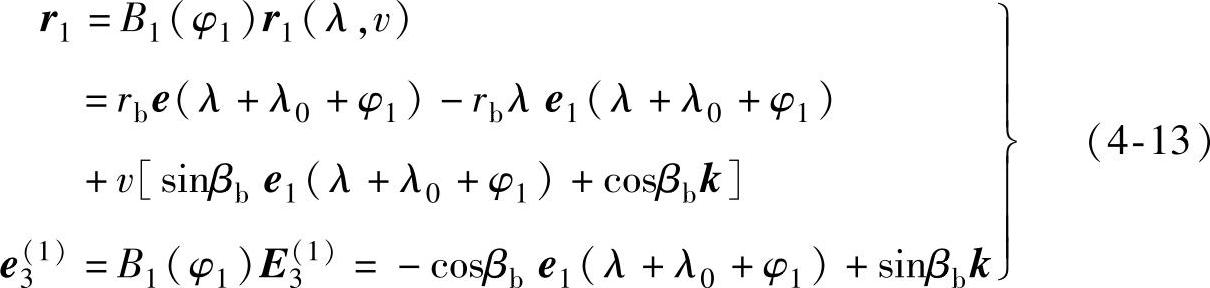
（2）刃边齿条

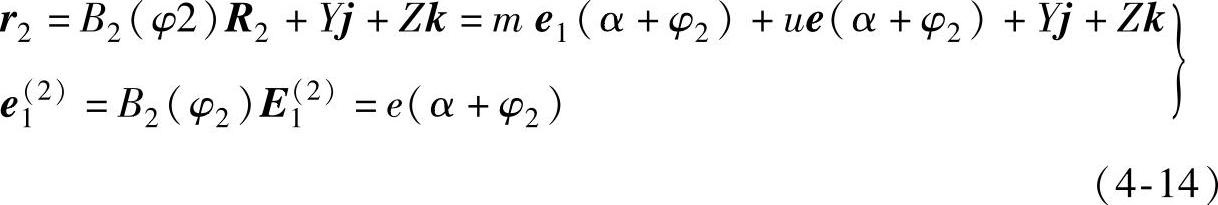
（3）啮合方程 此时刃边齿条与被测齿轮廓面在啮合点处满足接触条件与相切条件，于是有：

式（4-15）即为在理想条件下的啮合关系。

将式（4-13）、式（4-14）代入式（4-15），并使所有讨论归于图4-3中的O₁系内，有：

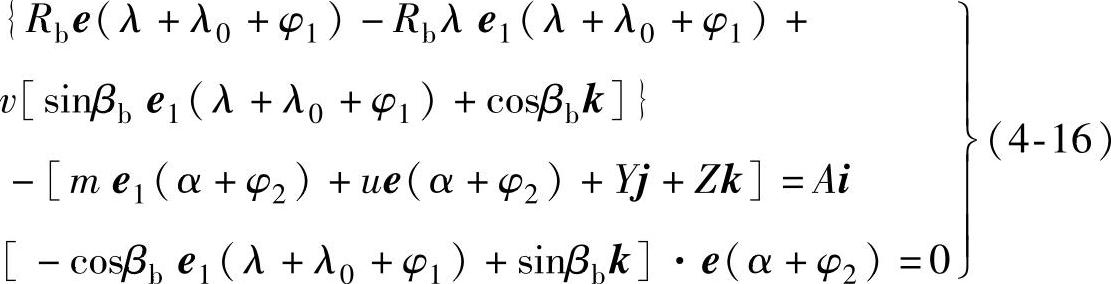
根据圆矢量函数纯积运算公式，由式（4-16）中第二式

可得：

sin[（α+φ₂）-（λ+λ₀+φ₁）]=0 （4-17）(www.xing528.com)

于是有

（λ+λ₀+φ₁）-（α+φ₂）=0

进而有

λ=（α+φ₂）-（λ₀+φ₁） （4-18）

将式（4-18）代入式（4-16）的第一式，经合并后可得

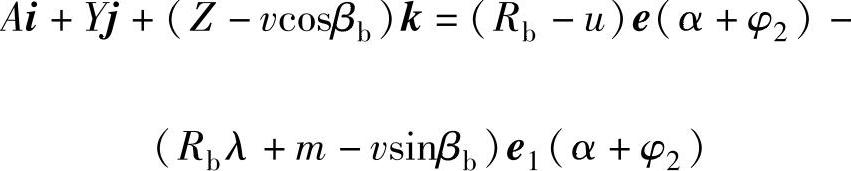
分别用e₁（α+φ₂）、i、k与上式两边作纯积，并根据式（4-18），经整理后可得

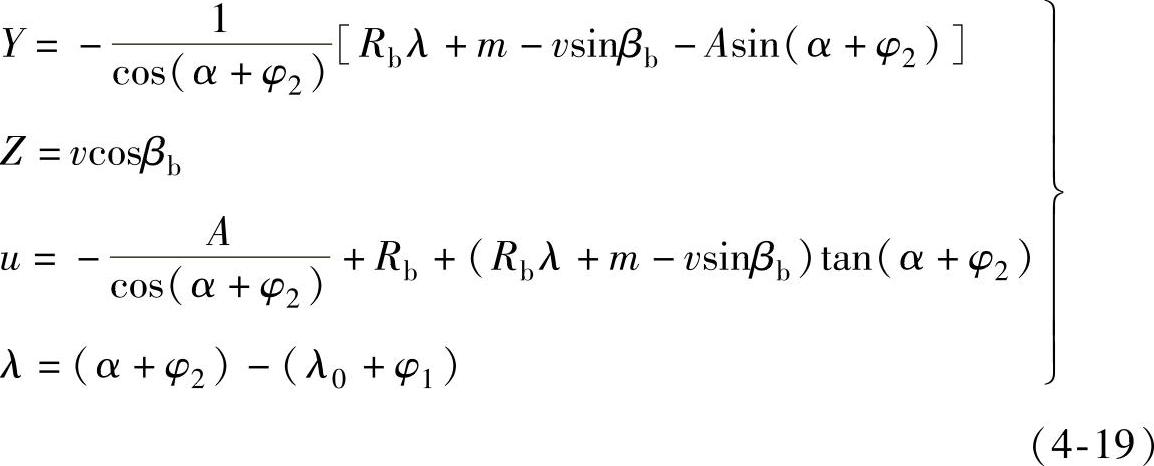
在式（4-19）中，由于α，λ₀为常数，齿轮的分度转角φ₁改变了啮合时的初始点相位角，齿条的转角φ₂改变了啮合角；当φ₁和φ₂确定后，Y和Z仅为参数v的函数，表明齿轮与齿条沿直母线啮合。消去参数v的影响，可求得Y和Z、φ₁、φ₂之间的关系为

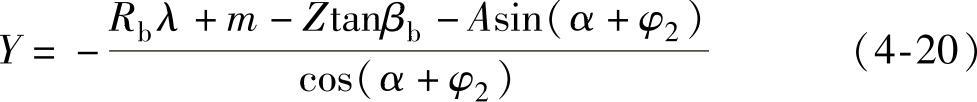
当φ₁和φ₂确定时，Y为Z的函数，二者坐标的合成确定了一条理论直母线；当φ₁或φ₂改变时，Y与Z的合成确定了廓面上的不同的直母线，构成直母线族。