被测齿轮与刃边齿条的廓面方程优化

1.被测齿轮廓面方程

由式（2-30），并考虑初始相位角的影响，可得无误差条件下被测齿轮廓面的一般表达式：

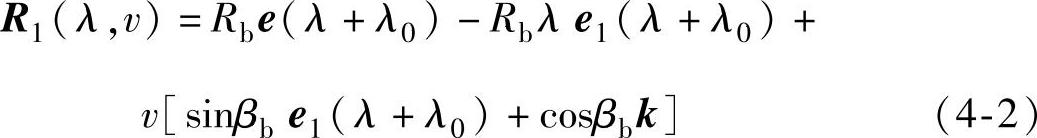
渐开线螺旋面的法向单位矢量为

E^（1）₃=-cosβ_be₁（λ+λ₀）+sinβ_bk （4-3）

因此，廓面的法向误差可写为

h=h（λ，v）E₃（1） （4-4）

式中，h（λ，v）为法向误差函数。

由此，误差条件下被测齿轮的廓面表达式可写为

R^∗₁=R₁（λ，v）+h（λ，v）E₃（1） （4-5）

根据渐开线齿轮精度标准，其齿廓偏差与螺旋线偏差都是在端面渐开线的法向度量的，根据式（2-26）可得端面渐开线的法线方向为

β=e₁（λ） （4-6）

因此，齿轮廓面的偏差形式可写为

f=f（λ，v）β=f（λ，v）e₁（λ） （4-7）

如图4-6所示，渐开线螺旋面的法向误差与端面渐开线法向误差的大小之间满足

f（λ，v）=h（λ，v）cosβ_b （4-8）

对于直齿轮，β_b=0°，h（λ，v）=f（λ，v），端面渐开线法向误差即为渐开线柱面的法向误差。(www.xing528.com)

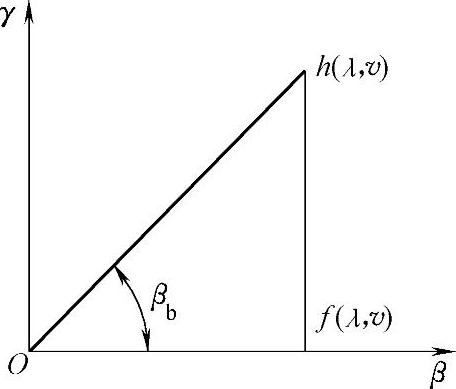
图4-6 廓面偏差

2.刃边齿条方程

在O₂坐标系中建立齿条测头刃边方程，如图4-7所示。无误差条件下，其方程为

R₂（u）=me₁（α）+ue（α） （4-9）

式中，m为齿条测头的结构参数，为常数；u为沿齿条刃边方向的标量参数；α为齿条测头的齿形角。

由式（4-9）可进而求得齿条测头的切线与法线方向的单位矢量为

由此，齿条测头的误差方程可写为

ε=ε（u）e₁（α） （4-11）

因此，误差条件下实际的齿条测头方程为

R^（2）=[m+ε（u）]e₁（α）+ue（α） （4-12）

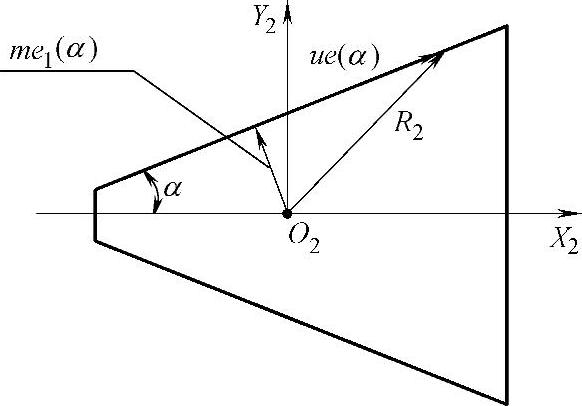
图4-7 刃边齿条

值得注意的是，由于法向误差的存在，导致被测齿轮与刃边齿条测头实际廓面的法线方向也发生变化，这将对实际啮合过程产生影响。考虑到其影响项为高阶，为了简化模型，这里对其忽略不计。