渐开线斜齿轮点啮合的原理解析

渐开线齿轮点啮合原理的主要特征为两轴线在空间呈交错状态，廓面间瞬时为点接触。渐开线齿轮点啮合原理的特点是齿面间有较大的接触应力和相对滑动速度，因此不利于齿轮传动，但有利于齿轮加工与测量，如蜗杆砂轮磨齿加工、滚齿加工、蜗杆式齿轮单面啮合综合测量等。

仍然采用媒介齿条的研究方法。此时，媒介齿条与渐开线螺旋面瞬时仍然相切接触于直母线上，不同之处在于，在交错轴条件下，与媒介齿条相啮合的两条瞬时接触线在空间不重合，二者的交点即为一对斜齿轮的接触点，如图2-5所示。因此，交错轴条件下，渐开线螺旋面间为点接触，瞬时接触点在空间固定坐标系的轨迹称为啮合线，在两廓面上的轨迹称为接触迹。由此可得出结论：啮合线有一条，而接触迹有两条。啮合线与接触迹成为研究渐开线齿轮点啮合原理的重要工具。

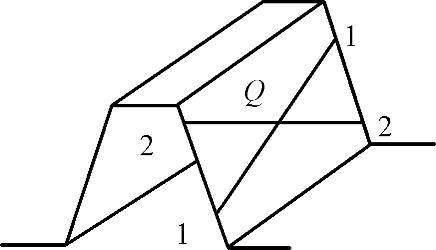
图2-5 媒介齿条

（1）渐开线齿轮点啮合的可分性 如果一对共轭曲面在位置条件变化之后仍能保持原来的传动比，这种性质称为可分性。所谓位置条件，主要指两个回转轴的中心距A以及轴交角∑。

前面已经讨论过，平行轴传动具有中心距可分性。而对于交错轴传动，不但满足中心距可分，还满足轴交角可分。对应有两类变位：中心距变位和轴交角变位。

交错轴斜齿轮啮合的可分性可表达如下：

互相呈交错轴啮合的一对渐开线螺旋面，在允许的啮合范围内，无论把它们放在怎样的中心距A和轴交角∑上，其传动速比都是恒定的。

根据交错轴斜齿轮啮合的可分性，其中心距可表达为

A=R₁+R₂+ΔA （2-44）

当ΔA=0时，称为规则啮合；当ΔA≠0时，称为非规则啮合。在规则啮合时，其中心距为两导出节圆柱半径之和，两个导出节圆柱相切，切点即为导出节点。这时两渐开线螺旋面轴线的公法线——中心距通过节点。规则啮合的这一特征与平行轴传动类似。

在规则啮合中，有一类特殊情况，即标准啮合。它是指两个啮合齿轮为标准齿轮，中心距及轴交角均为标准情况，这时导出节圆即为齿轮的分度圆。因此，标准啮合只是规则啮合的一个特例。

在非规则啮合时，两齿轮的导出节圆柱相交或相离，存在分离距ΔA；两条啮合线与两齿轮的中心距不再相交，而是沿齿向有一段移距。

（2）啮合线 由前述可知，媒介齿条与渐开线螺旋面之间为线接触，瞬时接触线在静止空间中的轨迹面称为啮合面。如图2-6所示，（M₁）、（M₂）分别为媒介齿条面与齿轮1和齿轮2的啮合面。啮合面具有如下特征：

1）啮合面与渐开线螺旋面基圆柱相切。

2）啮合面与媒介齿条面正交，交线即为直母线。

3）啮合面沿渐开线螺旋面圆周方向的位置由端面压力角决定。

两交错轴斜齿轮的啮合点既在（M₁）上，又在（M₂）上，因此（M₁）和（M₂）的交线N₁N₂即为啮合线。由此可得啮合线的性质：

1）啮合线为两基圆柱的内公切线。

2）由于啮合面与媒介齿条面正交，故啮合线必为媒介齿条的法线，即两廓面的公法线。

3）啮合线与两轮端面的夹角分别为β_b1、β_b2；啮合线在两端面的投影位置将由端面啮合角α_t1、α_t2确定。

4）对于规则啮合，两节圆相切，切点P称为节点。此时啮合线与中心距相交，交点即为节点。

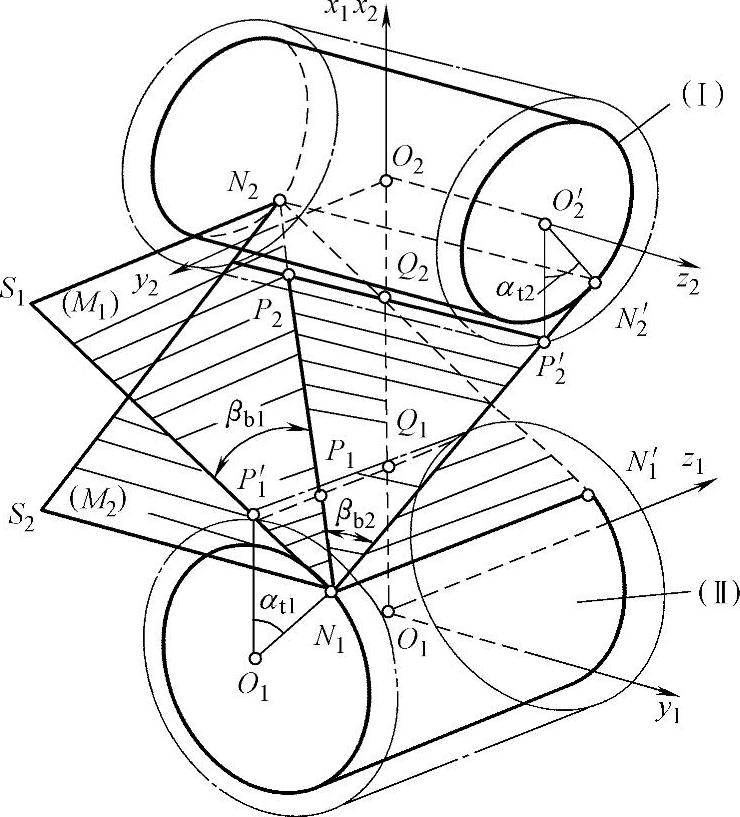
图2-6 啮合线与啮合面

根据啮合线的性质，不难求得其方程为

r=（R₁i-Hk₁）+u[-cosβ_b1e₁（α_t1）+sinβ_b1k₁] （2-45）

式中

(www.xing528.com)

令ΔA=0，H₁=0，即可得到规则啮合条件下的啮合线方程。

（3）接触迹 接触迹是瞬时啮合点在齿轮廓面上的轨迹，它实质为渐开线廓面上的一条特殊曲线，因此，接触迹的求解实质为求渐开线螺旋面上参数λ和v之间关系的过程。

首先可以令渐开线廓面绕其轴线回转角度φ，求其与啮合线的交点，必为瞬时啮合点；然后令瞬时啮合点绕轴线逆向回转φ角，使其回到原始位置，则必为接触迹上的点。当φ取不同的值时，可获得廓面上的一条接触迹。

在规则啮合条件下，设两廓面（∑₁）、（∑₂）于节点P处啮合时为零位，此时φ₁=φ₂=0°，表示在零位处O₁x₁y₁、O₂x₂y₂面内两截形为渐开线。δ₀₁、δ₀₂为初始相角，由图2-7可得：

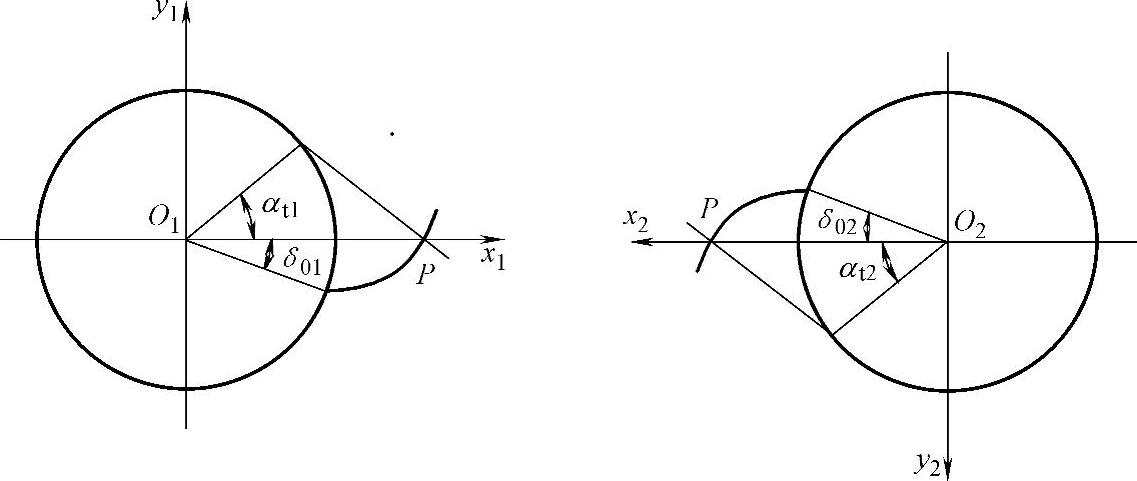
图2-7 初始相位角

在上述规定下，参考式（2-30），渐开线螺旋面方程可写为

R（λ，v）=R_be（λ-δ₀）-R_bλe₁（λ-δ₀）+v[sinβ_be₁（λ-δ₀）+cosβ_bk] （2-48）

令渐开线螺旋面方程绕轴线回转角度φ，根据回转群的性质可得：

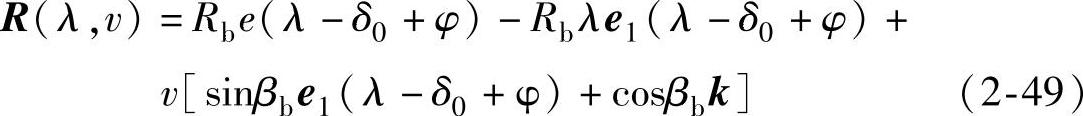
下面求渐开线螺旋面与啮合线的交点。令啮合线方程（2-45）中的H₁=0，并令其与上式各坐标分量相等，则有

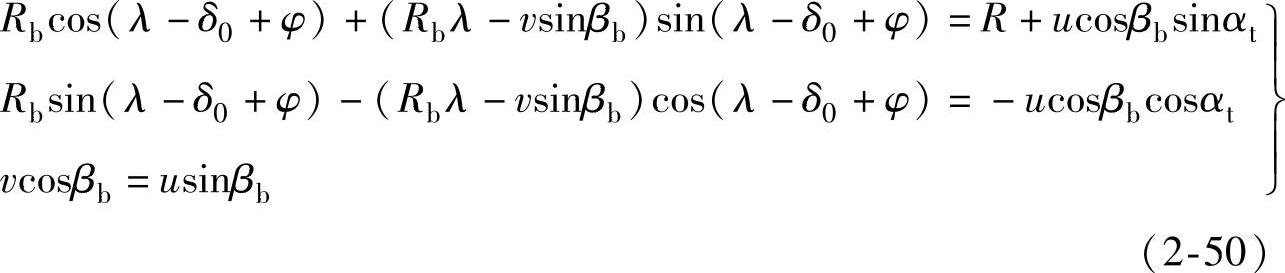
对式（2-50）求解，首先由第三式可求得

对式（2-50）第一式和第二式左右两边求平方和，并将式（2-51）代入，根据式（2-41），经化简后可求得

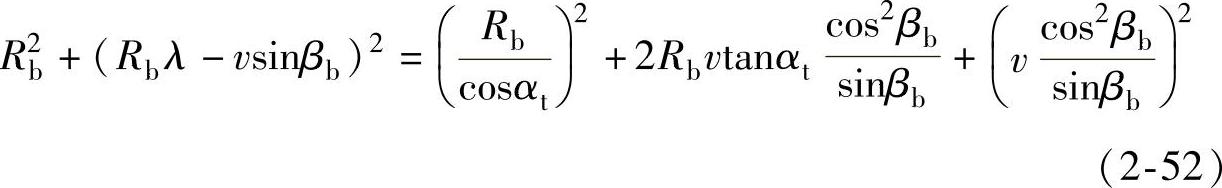
进而有

v=R_bsinβ_b（λ-λ₀） （2-53）

式中，λ₀=tanα_t，为常数。

式（2-53）描述了不同瞬时的啮合点在渐开线螺旋面上应满足的参数条件，称为接触条件。将其代入渐开线螺旋面方程式（2-48），即可得到接触迹方程：

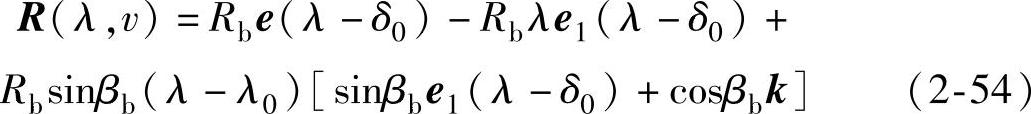
分析式（2-54），可得接触迹的如下性质：

1）渐开线螺旋面上的接触迹形状仅由其基圆半径和基圆螺旋角决定，而同与之啮合的另一螺旋面参数及中心距、轴交角无关。

2）由式（2-53）可知，当β_b=0°时，v=0，表明交错轴传动中的直齿轮廓面上的接触迹即为端面渐开线。

3）当β_b≠0°时，表示交错轴斜齿轮副中的蜗杆或斜齿轮的接触迹不再是渐开线。此时，斜齿轮的接触迹为廓面上倾斜的曲线，蜗杆的接触迹为一条复杂的蜗旋线。

渐开线齿轮点啮合原理对研究齿轮滚齿加工原理、测量原理及分析误差成因、提高加工精度有重要意义。