下面讨论渐开线螺旋面的一些重要性质。
1.可展性
根据式(2-30),当λ=常数时,Rp(λ)与m均为常矢量,前者描述渐开线上的一个固定点,后者描述该点法面内的一个确定方向,因此R(λ,v)描述渐开线螺旋面上的一条直母线;又由式(2-31)可以看出,此时e3为常矢量,表明渐开线螺旋面沿直母线的法线方向恒定。根据微分几何学,沿直母线上各点具有公共法线方向的直纹面称为可展面,曲面的这种性质称为可展性。工程上常用的柱面、锥面,以及渐开线螺旋面都属于可展面的范畴,此类曲面因具有可展性和优良的工艺性在工程上得到广泛应用。
可展面沿直母线各点处的法线方向恒定,因此,过直母线有唯一的切平面,必然为单参数平面族的包络面。渐开线螺旋面的可展性为采用平面包络法加工以及后文采用直线型刃边测头进行综合测量提供了方便。
2.特征线
令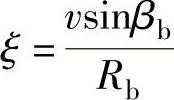 ,ζ=λ-ξ,这时,式(2-30)可化为
,ζ=λ-ξ,这时,式(2-30)可化为
R(ξ,ζ)=Rbe(ξ+ζ)-Rbζe1(ξ+ζ)+Rbξcotβbk (2-32)
当v=常数时,ξ=常数,对比式(2-25),式(2-32)表示初始相位角为ξ的渐开线,此时z=Rbξcotβb为常数,表明渐开线螺旋面的端面截形为渐开线。
当ζ=常数时,式(2-32)可进一步转化为
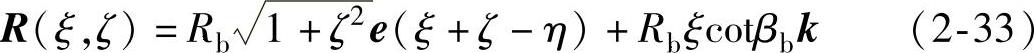
式中,η=atanζ,为常数。
式(2-33)表示半径为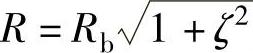 的圆柱上螺旋常数为h=Rbcotβb的螺旋线。
的圆柱上螺旋常数为h=Rbcotβb的螺旋线。
当λ=常数时,由上面的分析可知,式(2-30)描述渐开线螺旋面上的一条直母线。
综上所述,渐开线螺旋面不同的参数为常数时,方程分别描述直母线族、渐开线族和螺旋线族,构成了曲面上的三族曲线。其中渐开线族和螺旋线族构成了渐开线齿轮的齿形和齿向;直母线族构成了平行轴传动时的瞬时接触线,是评价齿轮承载能力的重要指标。大型齿轮综合测量的实质正是通过测量廓面上的直母线族误差,进而通过分离获得齿廓偏差和螺旋线偏差。
3.曲率特征
对渐开线螺旋面的矢径及标架式(2-29)和式(2-30)求微分,并注意圆矢量函数的微分式(2-15),可得(https://www.xing528.com)
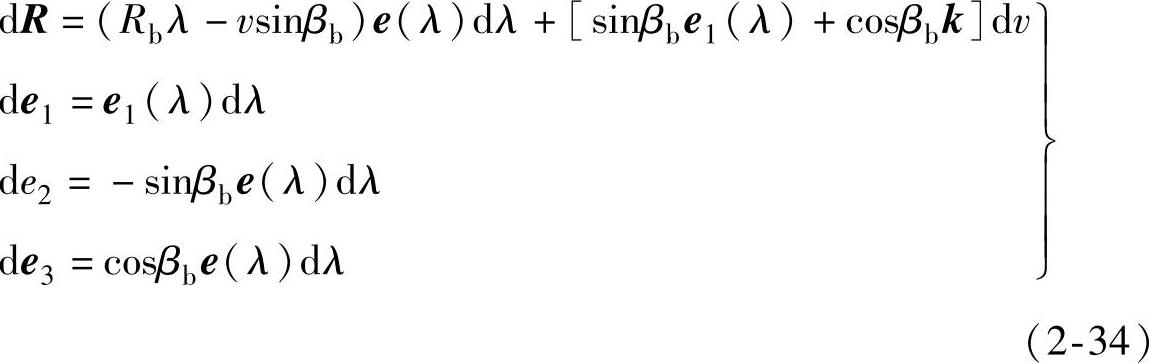
代入式(2-17)、式(2-20)可进而求得标架的无穷小运动
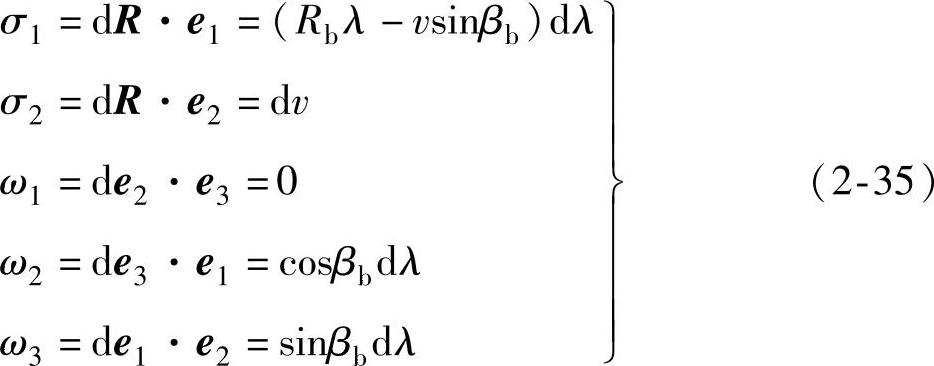
代入式(2-22),首先可求得
τg1=0
上式表明渐开线螺旋面上e1、e2所对应的渐开线方向与直母线方向必为其主方向,其对应的法曲率必为曲面的主曲率。由式(2-22)可进而求得
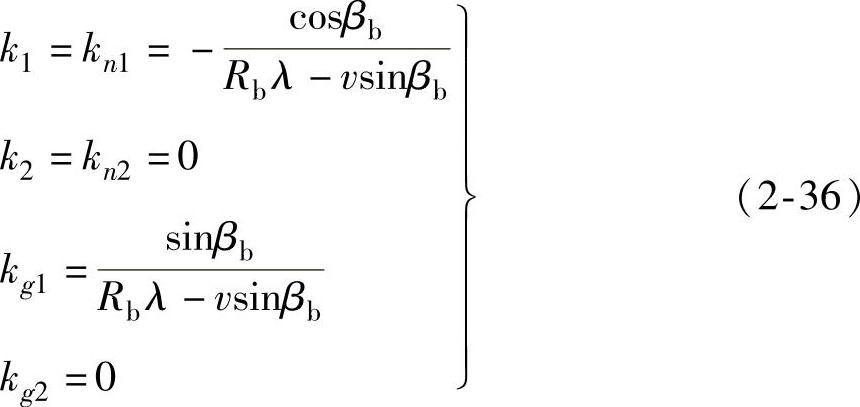
式中,k1等式前面的负号表示渐开线方向的主曲率与e3规定的正方向相反;k2=0描述沿直母线方向的主曲率为零。对k1求负倒数,尚可求得该方向的曲率半径为

其几何意义如图2-4b所示。直角三角形ABC构成了基圆柱的切平面,称为渐展三角形。由此可得出结论:渐开线螺旋面沿直母线各点的非零主曲率的中心同处于直线BC上,称为曲率轴;曲面上的渐开线族与直母线族构成了曲面的正交曲线网,且为曲面的曲率线;由于可展面沿直母线方向的主曲率kb2=0,因此其总曲率K恒等于零。微分几何学指出,总曲率为零的曲面是唯一可展开为平面的曲面,可展面也因此而得名。
上面讨论了渐开线螺旋面的方程及其特征,由式(2-30)可以看出,渐开线螺旋面的形状由基圆半径Rb和基圆螺旋角βb两个基本参数决定。特殊的,当βb=0时,式(2-30)表示渐开线柱面,它构成了渐开线直齿轮的廓面。此时有:
R(λ,v)=Rbe(λ)-Rbλe1(λ)+vk (2-38)
此时的直母线族与螺旋线族重合,均平行于齿轮轴线。其曲率特征为
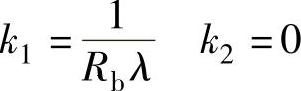
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




