渐开线直齿轮、渐开线斜齿轮、渐开线蜗杆等廓面都是由渐开线螺旋面所组成(渐开线柱面认为是螺旋角为零的特殊螺旋面)。一般认为,渐开线螺旋面是由端面渐开线绕基圆柱做螺旋运动所形成。为了研究方便,本文将其认为是位于渐开线法面内且与端面夹定角的直母线沿渐开线运动所形成的直纹面。
如图2-4a所示,与基圆相切的一条直线绕基圆做纯滚动时,其上一点的轨迹称为渐开线,该直线称为渐开线的发生线。渐开线方程可由圆矢量函数表示为
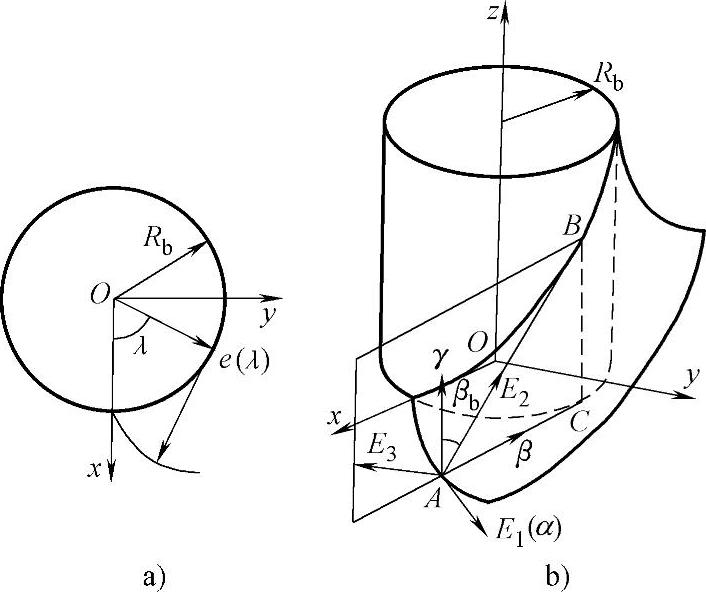
图2-4 渐开线与渐开线螺旋面
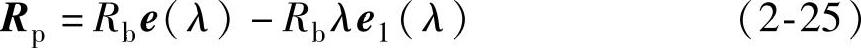
式中,Rb为基圆半径;λ为展开角。
在渐开线上建立Frenet标架{Rp(λ),α,β,γ},α、β、γ分别为渐开线的单位切矢、主法矢和副法矢。容易求得

利用曲线的标架微分公式,可求得渐开线的曲率与挠率为

式中,挠率τ=0,表明渐开线为平面曲线。
对曲率求倒数,尚可获得其曲率半径为
ρ=Rbλ(https://www.xing528.com)
参考图2-4a,表明渐开线的曲率中心位于发生线与基圆的切点处。
令渐开线法面{βγ}内的一条直母线沿渐开线运动,且保持与β轴的夹角为定值,如图2-4b所示。则直母线的单位矢量可写为
m=cosθβ+sinθγ (2-28)
式中,θ为直母线与e2轴的夹角,为定值。
由此获得的渐开线螺旋面方程为
R(λ,v)=Rp(λ)+vm=Rp(λ)+v(cosθβ+sinθγ) (2-29)
式中,v为沿直母线方向的长度参数,θ的几何意义为渐开线螺旋面基圆螺旋升角。
将式(2-25)、式(2-28)代入式(2-29),并令βb=π/2-θ,βb为基圆螺旋角,可得渐开线螺旋面的一般表达式
R(λ,v)=Rbe(λ)-Rbλe1(λ)+v[sinβbe1(λ)+cosβbk] (2-30)
根据渐开线螺旋面上渐开线与直母线的正交性,在曲面上建立标架{R(λ,v),e1,e2,e3},其中e1、e2为渐开线与直母线的单位切矢,e3为单位法矢,三者构成右手正交系。根据式(2-26)、式(2-28),可求得其标架方程为
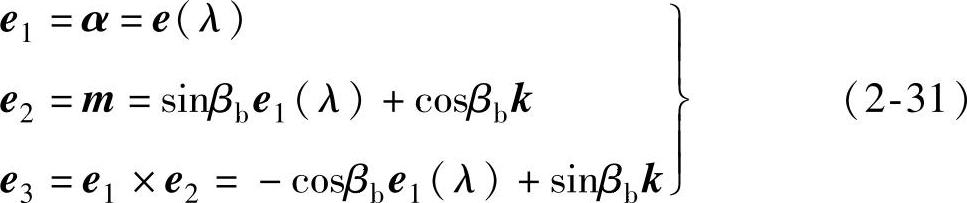
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




