回转矢量微分式：共轭曲面原理研究的关键公式

1.回转运动群

如图2-1所示，设矢量R绕单位矢量为Ω₀的轴回转φ角后变为矢量r，则有

r=B（φ）R （2-1）

式中，B（φ）称为回转运动群，简称回转群。

回转群属于合同变换群的一种，因而满足群公理，即具有封闭性，满足结合律，并存在幺元及逆元。回转群描述了刚体的回转运动，其中B（0）=E，E称为恒等变换群，它描述了“不回转”，即相对静止；B（-φ）=B^-1（φ），称B^-1（φ）为逆回转群，它描述逆向回转运动。回转群的这些特征为研究共轭曲面原理带来了很大的方便。

图2-1 回转运动群

在已知正交标架{O，i，j，k}中，回转轴OP的单位矢量Ω₀可表示为

Ω₀=ω₀₁i+ω₀₂j+ω₀₃k （2-2）

式中，ω₀₁、ω₀₂、ω₀₃为Ω₀的坐标分量，且满足。

2.回转群的基本性质

回转群存在如下基本性质：

1）B（φ）Ω₀=Ω₀，即回转轴上的矢量，回转后保持不变。

2）B（φ₁）B（φ₂）=B（φ₁+φ₂）。

3）[B（φ）a]·[B（φ）b]=a·b，即两矢量的纯积与回转无关。

4）[B（φ）a]×[B（φ）b]=B（φ）（a×b），即两矢量回转后的矢积等于矢积的回转。

5），，其中，λ为三阶反对称矩阵，可由回转轴的坐标分量表示为

λ矩阵具有重要性质：λR=Ω₀×R。因此有

(https://www.xing528.com)

3.回转群的矩阵表示

回转群有多种表示方法，其中矩阵表示法为应用最广泛的一种，下面讨论绕z轴回转时的矩阵表示。

图2-2 矢量绕z轴的回转

如图2-2所示，设矢量R绕z轴回转φ角后变为矢量r，其坐标表示为

式中，X、、Y、Z为R的坐标分量；x、y、z为r的坐标分量。

利用转轴公式可以求得

写成矩阵形式则有

由此可得

式（2-8）中的B（φ）即为回转轴为z轴时回转群的矩阵表示。

4.回转矢量的微分形式

对式（2-1）两边微分，并根据式（2-4）可得

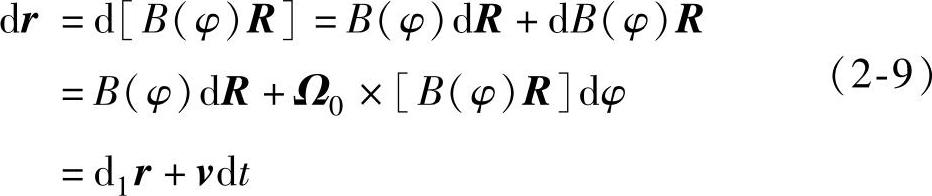
式中，d₁r=B（φ）dR，称为相对微分，描述矢径端点的位置变化量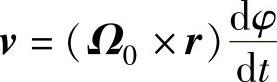；，为矢径端点处的回转线速度；dt为时间微分。

式（2-9）即为回转矢量的微分形式，它成为研究共轭曲面原理的重要公式。