超滤的传质基础理论

（一）浓差极化模型

超滤分离中，由于筛分作用，料液中的部分大分子溶质被膜截留，溶剂及小分子溶质能自由地透过膜，表现出超滤膜的选择性，截留物在膜表面累积增多，膜表面料液浓度逐渐上升，在浓度梯度作用下，近膜表面的溶质又以相反方向向料液扩散，平衡状态时膜表面形成一定的溶质浓度分布边界层，对溶剂等小分子的运动起阻碍作用，如图5-2所示，这种现象称为浓差极化。浓差极化对超滤膜性能有很大影响，当膜面上截留溶质的浓度增加到一定值时，在膜面上会形成一层凝胶层，该凝胶层对料液流动产生很大阻力，因而使得膜透过通量急剧下降。

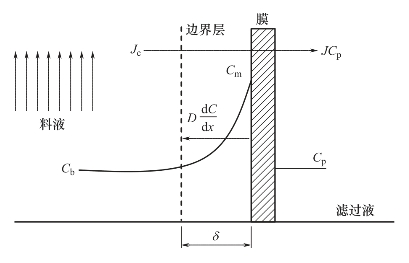
图5-2　浓差极化现象示意图

由于浓差极化现象的存在，膜表面截留的溶质浓度为Cm，所以膜的真实截留率R应为：

截留率R虽然能真实地表示超滤的特性，但由于膜表面浓度无法测定，所以可按图5-2所示的浓差极化模型进行计算。

膜表面被截留的溶质，会沿浓度梯度向料液方向扩散，当溶质以对流方式向膜方向的传递量等于渗透通量与反向扩散通量之和时，扩散得到平衡：

式中：C——溶质质量浓度，mg/L；

J——膜透过通量，m3/（m2·s）；

D——扩散系数，m2/s。

边界条件为：x=0C=Cm

x=δC=Cb

将边界条件代入式（5-2）积分，可得到下列浓差极化方程式：

其中，扩散系数D与边界层厚度δ之比为传质系数，即K=D/δ。引入传质系数K和真实截留率，式（5-3）则为：

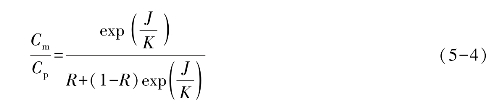
式中：Cm/Cp称为浓差极化模数，随着通量J增大，截留率R增加以及传质系数K减小，浓差极化模数增大，即膜表面的浓度Cm增大。

当溶质被膜完全截留时（即R=1和Cp=0），式（5-3）则为：

（二）传质系数

浓差极化层内的传质系数K，受体系流体力学状况影响较大，可以采用传质系数并联式计算，当膜组件内的流动为层流时，可用莱维科式进行计算：

式中：Sh——舍伍德数（=Kdh/D）

Re——雷诺数（=Udh/γ）；

Sc——施密特数（=γ/D）；

dh——当量直径，m；

L——膜的长度，m。

式（5-6）的适应范围为：1000＜Re、Sc、dh/L＜5000。由式（5-6）求得的传质系数是沿膜长L的平均值。

湍流时可按照德斯来尔提出的方程进行计算：

实际使用的膜组件，除了管式和中空纤维式外，一般在流道中要加入湍流促进材料，以增加湍流程度，提高传质系数K。

（三）速率方程

膜透过速率方程式，可以从不可逆过程热力学现象论方程式推导如下：

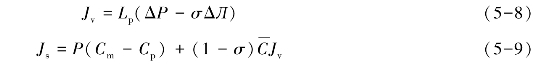
式中：Lp——纯水渗透系数，m3/（m2·Pa·s）；

P——溶质渗透系数，m/s；(www.xing528.com)

σ——反射系数，通常为0～1；

——膜两侧溶质平均浓度，mg/L。

当膜两侧浓度差较大时，可用式（5-10）代替式（5-7）：

式中：

式（5-10）和式（5-11）表明，随着压力的增加，透过膜的通量Jv增大时，真实截留率R也增大，式（5-8）、式（5-10）和式（5-11）可以作为表示截留率的速率方程式使用，也包括高截留率的情况在内。

（四）微孔模型

超滤膜的渗透机理基本上是“筛分机理”，通常用微孔模型来评价膜性能。纯水渗透系数是膜的固有值，而溶质渗透系数及反射系数是由溶质决定的数值。在微孔模型中，假定膜中半径rp、长Δx的圆筒形微孔是贯穿孔。溶质为半径rs的刚体球，溶液在微孔内的流动为泊谡叶（Poiseuille）流动，溶质的反射系数及渗透系数可分别表示如下：

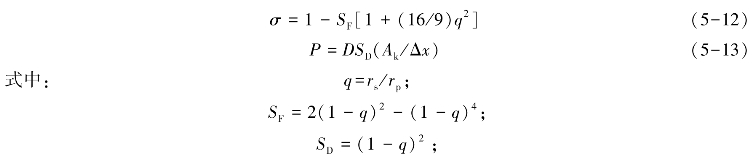
Ak——单位膜面积上所有微孔的截面积（即孔隙率）；

rs——可根据溶质为刚性球的假设，用斯托克斯（Stocks）半径公式来表示为：rs=kT/6ЛμD。

其中：k——波尔茨曼常数（=1.38×10-23）；

T——绝对温度，K；

Л——渗透压，MPa；

μ——黏度，g/（cm·s）；

D——扩散系数，m2/s。

另外，根据泊谡叶定律，纯水渗透系数可表示为：

式中：rp——膜的微孔半径，mm；

Ak——单位膜面积的全部微孔截面积；

μ——黏度，g/（cm·s）。

对于表征膜特性的rp及Ak/Δx为已知的膜，任何溶质都可以用式（5-12）、式（5-13）和式（5-14）计算截留率，溶质的特性可以用其扩散系数表示。

（五）渗透压模型

超滤的溶质是高分子，因此低浓度时其渗透压与操作压力相比可忽略不计，随着溶液浓度升高，渗透压成指数关系急剧上升，因此用超滤浓缩时必须考虑渗透压的影响。

高分子溶液的渗透压，通常可表示为：

在超滤浓缩过程中应用时，溶质截留率一般为100%，所以式（5-10）中的σ=1，渗透压差（Δx）变为与膜面浓度相对应的渗透压，即式（5-8）可改写为：

使浓差极化式（5-3）中的Cp=0，可得到下列膜表面浓度计算式：

当操作压力、原料液浓度及式（5-17）联立求解透过膜的通量，式（5-17）中的传质系数K可通过式（5-8）或式（5-9）求得。

用纯水测定透过膜的通量时，其值与操作压力成比例增加，但用高分子溶液进行超滤时透过膜的通量与压力不成比例，在达到某一定值后，就不随压力变化了。并且这个值与膜的渗透阻力（纯水渗透系数的倒数）也无关。此时膜的透过通量，称为极限通量。它随着料液浓度增高而变小，随着膜表面的传质条件改变而变大。

（六）凝胶极化模型

当膜表面溶质浓度Cm达到溶质的凝胶浓度时（Cg），式（5-3）可表示为：

形成凝胶层时，溶质截留率极高，即Cp=0，上式简化为：

式（5-19）称为凝胶极化方程式，凝胶浓度Cg决定于溶质的性质，在一定压力下极限通量Jlim与主体料液浓度Cb的关系是一条斜率为K的直线。