B样条曲线模型的C2连续性条件

1.插值曲线

数学上插值函数的定义如下:

已知离散函数

y_i=f(x_i)(i=0,1,2,…,n)构造函数φ(x),满足条件

φ(x)=y_i=f(x_i)(i=0,1,2,…,n)则称φ(x)为插值函数。i为插值节点,即离散点。通过n+1个插值节点构造的函数

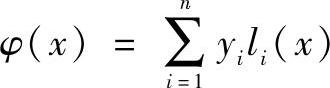
称为拉格朗日插值,其中l_i(x)为插值基函数。

通过两个离散点可构造直线,通过三个离散点可构造二次插值曲线。离散点越多,曲线变得越光滑,但计算量大,同时计算误差累计量增大。采用分段插值方法可减小计算量,但需保证离散点连接处的光滑性。

2.三次样条曲线

分段插值存在着一个缺点,就是会导致插值函数在子区间的端点(连接处)不光滑,即导数不连续。对于一些实际问题,不但要求一阶导数连续,而且要求二阶导数连续。为了满足这些要求,人们引入了样条插值的概念。

样条(spline)是工程绘图中的一种工具,是有弹性的细长木条。绘图时,用细木条连接相近的几个节点,然后再进行拼接,连接全部节点,使之成为一条光滑曲线,且在节点处具有连续的曲率。样条本质上是一段一段的三次多项式拼合而成的曲线,在拼接处,不仅函数是连续的,且一阶和二阶导数也是连续的。

设f(x)是区间[a,b]上的一个连续可微函数,在区间[a,b]上给定一组节点a=x₀<x₁<x₂…<x_n=b,设函数S(x)满足条件:

1)S(x)在每个子区间[x_i,x_i+1](i=0,1,2,…,n-1)上是次数不超过m的多项式。

2)S(x)在区间[a,b]上有m-1阶连续导数。则称S(x)是定义在区间[a,b]上的m次样条曲线,x₀,x₁,x₂…,x_n称为样条节点,其中x₁,x2…,x_n-1称为内节点,x₀,x_n称为边界节点。

当m=3时,便成为最常用的三次样条曲线。

设给定区间[a,b]上n+1个点a=x₀<x₁<x₂…<x_n=b,以及相应的函数值y_i=f(x_i)(i=0,1,…,n)。如果函数S(x)满足条件:

1)在每个子区间[x_k,x_k+1](k=0,1,…,n-1)上,S(x)是不超过三次的多项式,且S(x_i)=y_i(i=0,1,…,n)。

2)S(x)、S′(x)、S″(x)在[a,b]上连续。则称S(x)是f(x)在节点x₀,x₁,x₂…,x_n上的三次样条插值函数。

3.贝塞尔(Bezier)曲线

贝塞尔曲线是逼近法的典型例子。

已知n+1个有序离散点(节点)P₀(x₀,y₀),P₁(x₁,y₁),…,P_n(x_n,y_n),借助一组伯恩斯坦(Bernstein)基函数

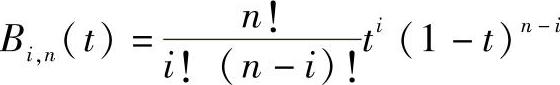
可定义贝塞尔曲线

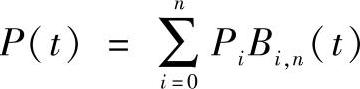
其中,P_i(i=0,1,…,n)称为控制点或贝塞尔点。依次连接n个控制点形成的空间折线称为控制多边形,如图2-4所示。

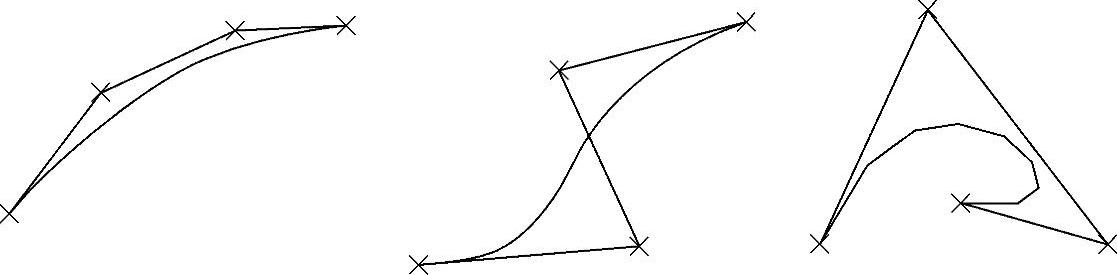
图2-4 三次贝塞尔曲线的控制多边形

贝塞尔曲线的特点如下:

1)曲线通过起点和终点两个控制点。

2)贝塞尔曲线在两端点相切于控制多边形,其余点定义曲线的导数、形状和阶次。

3)凸包性,即贝塞尔曲线形状的趋向仿效贝塞尔特征多边形形状,曲线不会在贝塞尔多边形之外。

4)几何不变性,即贝塞尔曲线的几何特征不随坐标变化而变化。

5)可分割性,即在一段贝塞尔曲线中间某一点处分割成两段,每一段仍为贝塞尔曲线,且无限可分。

当n=3时,P₀、P₁、P₂、P₃四个控制点可构造一条三次贝塞尔曲线,可以表示为(www.xing528.com)

贝塞尔曲线适于自由曲线的外形设计,是目前计算机辅助几何设计中的主要方法之一。

4.B样条曲线

虽然贝塞尔曲线具有许多优越性,但也有三个缺点:

1)若变动贝塞尔特征多边形的某个顶点,则影响整个曲线形状。

2)贝塞尔曲线缺乏灵活性,缺少局部修改外形的能力。

3)当特征多边形的顶点数量多时,多边形对曲线的控制能力减弱。

1973年,里森费尔德(R.F.Riesenfeld)在研究贝塞尔曲线的基础上,改进了贝塞尔曲线,提出B样条曲线。该曲线采用特征多边形和基函数来定义,所用的基函数是B样条基函数。B样条曲线较贝塞尔曲线更为优越,特点在于多项式的阶次可不受控制点数的限制。它使设计的曲线具有局部修改能力和更大的灵活性,同时也容易保证曲线的连续性,简化曲线的光滑拼接问题。

已知n+1个控制点P_i(i=0,1,…,n),也称为特征多边形的顶点,k阶B样条曲线的表达式为

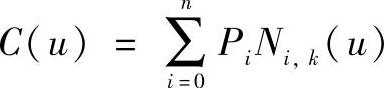
其中,N_i,k(u)为调和函数,也称为基函数,可定义为

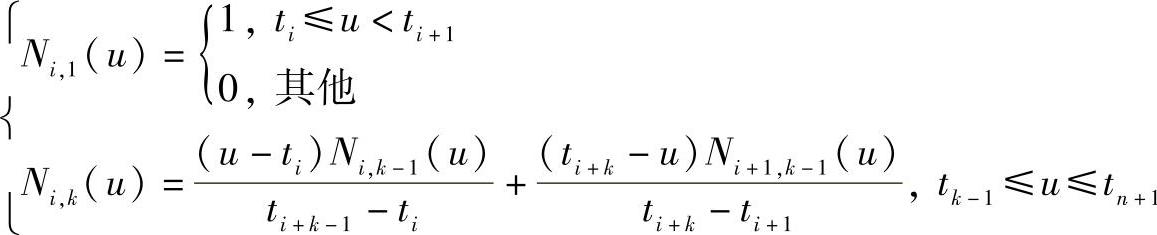
其中,t_i是节点值,T=[t₀,t₁,…,t_n+k]构成了k阶B样条函数的节点矢量。其中的节点是非均匀序列。当节点沿参数轴是均匀等距分布时,则表示均匀B样条函数;当节点沿参数轴的分布是不等距分布时,则表示非均匀B样条函数。

B样条曲线特点如下:

1)局部性,即k阶B样条曲线上的一点,只被相邻的k个顶点所控制,与其他控制顶点无关。当移动一个顶点时,只对其中的一段曲线有影响,对整个曲线的其他部分没有影响。

2)C2连续性,即B样条曲线各段之间是以位置、斜率与曲率连续为条件的,故具有C2连续性。

3)凸包性,即B样条曲线的凸包是定义各曲线段的控制顶点的凸包的并集,B样条曲线恒位于它的凸包内,比贝塞尔曲线的凸包性更强。

4)几何不变性,即B样条曲线的几何特征不随坐标变换而变化。

5)可分割性,即可以将一段B样条曲线在其中间某一点处分割为两段,每一段仍然为一段新的B样条曲线。

5.NURBS曲线

贝塞尔曲线和B样条曲线不能够精确表示除抛物线外的二次曲线弧,只能给出近似的表示,导致设计误差。通过对B样条方法的改造,保留其描述自由型形状的优点,扩充其统一表示二次曲线弧的能力,形成了有理B样条方法。由于在形状的实际描述中,更多地以非均匀类型出现,称为非均匀有理B样条(Non-Uniform Rational B-Spline)方法,简称NURBS方法。

一条k次NURBS曲线是由分段有理B样条多项式基函数定义的,其形式为

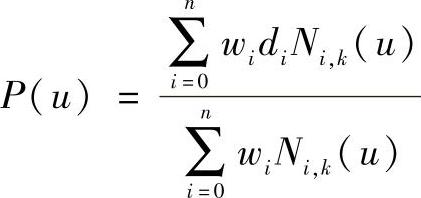
其中,w_i(i=0,1,…,n)称为权或权因子,分别与控制顶点d_i(i=0,1,…,n)相联系。N_i,k(u)为k次规范B样条基函数。

NURBS方法主要有以下四个特点:

1)NURBS不仅可以表示自由曲线、曲面,它还可以精确地表示圆锥曲线和规则曲线,所以NURBS为计算机辅助几何设计提供了统一的数学描述方法,在计算机图形学领域和CAD/CAM中获得了广泛的应用。

2)NURBS具有影响曲线、曲面形状的权因子,故可以设计相当复杂的曲线和曲面形状。若运用恰当,将更便于设计者实现自己的设计意图。

3)NURBS方法是非有理B样条方法在四维空间的直接推广,多数非有理B样条曲线曲面的性质及其相应的计算方法可直接推广到NURBS曲线和曲面。

4)计算稳定且快速。

然而,NURBS也存在一些缺点:

1)需要额外的存储以定义传统的曲线和曲面。

2)权因子的选择不恰当可能导致很差的参数化结果,甚至毁掉后续的曲面结构。